Практическая работа

Тема: Решение прикладных задач на применение комплексных чисел: расчет цепей синусоидального тока.

Цель: Научиться  выполнять расчеты цепей переменного тока с применением комплексных чисел.

Обеспечение практической работы: методические указания  для практической работы, средства вычислительной техники, линейка, карандаш. Порядок выполнения работы:

1.                 Записать в тетрадь тему и цели практической работы.

2.                 Повторить теоретический материал по теме практической работы.

3.                 Ознакомиться с методикой решения задач.

4.                 Решить задачи самостоятельно.

5.                 Ответить на контрольные вопросы.

Сведения из теории:

В технике встречаются различные формы переменного тока, однако наиболее распространен сегодня ток переменный синусоидальный, именно такой используется всюду. При помощи него электроэнергия передается, в виде переменного тока она генерируется, преобразуется трансформаторами и потребляется нагрузками. Синусоидальный ток периодически изменяется  по синусоидальному (гармоническому) закону.

𝑖𝑖(𝑡𝑡) = 𝐼𝐼_𝑚𝑚𝑆𝑆𝑖𝑖𝑆𝑆𝜔𝜔𝑡𝑡 +ψ_𝐼𝐼 𝑢𝑢(𝑡𝑡) = 𝑈𝑈_𝑚𝑚𝑆𝑆𝑖𝑖𝑆𝑆𝜔𝜔𝑡𝑡 +ψ_𝑈𝑈

i, u – мгновенные значения тока и напряжения I_m,, U_m  - амплитудные значения тока и напряжения ψ_𝐼𝐼,ψ_𝑈𝑈 - начальные фазы тока и напряжения

Действующие значения тока и напряжения меньше амплитудных значений в корень из двух раз:

                                                                                                            𝐼𝐼                     𝑈𝑈

𝐼𝐼 ; 𝑈𝑈

Одним из способов расчета цепей переменного тока является комплексный метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений.

В комплексном методе действующее значение токов и напряжений записывают так:

𝐼𝐼̇ = 𝐼𝐼𝑒𝑒𝑗𝑗ψ𝐼𝐼 𝑈𝑈^̇ = 𝑈𝑈𝑒𝑒^𝑗𝑗ψ𝑈𝑈

j – мнимая единица в электротехнике

Из закона Ома определяют комплексное значение сопротивления:

                                                                                         𝑍𝑍 = 𝑈𝑈̇        𝑗𝑗𝑗𝑗

= 𝑍𝑍𝑒𝑒

𝐼𝐼̇

𝜑𝜑 = ψ_𝑈𝑈 −ψ_𝐼𝐼

Z - модуль комплексного сопротивления

Сложение и вычитание комплексных чисел осуществляется в алгебраической форме, а умножение и деление в показательной форме.

Задание

Определить комплексным методом ток в цепи (рис. 1)  и построить векторную диаграмму. Данные варианта взять из таблицы 1. Расчет цепи выполните, используя пример.

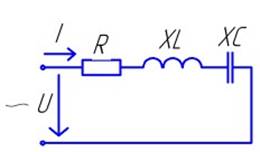
Рис.1

Таблица 1

Порядок расчета

1.        Определить общее сопротивление цепи в комплексной форме.

2.        Определить ток цепи (закон Ома в комплексной форме).

3.        Определить напряжения U_R, U_L и U_C  в комплексной форме.

4.        Построить векторную диаграмму с учетом характера нагрузки и масштаба.

Пример расчета цепи с применением комплексных чисел Дано: сопротивление резистора R = 8 Ом, индуктивное сопротивление катушки  X_L = 6 Ом, емкостное сопротивление  конденсатора X_C = 8 Ом, напряжение питания цепи U = 80 В. Определить символическим методом ток в цепи, построить векторную диаграмму. Решение:

1.     Определяем комплекс полного сопротивление цепи:

𝑍𝑍 = 𝑅𝑅 + 𝑗𝑗(𝑋𝑋_𝐿𝐿 − 𝑋𝑋_𝐶𝐶) = 8 + 𝑗𝑗(6 − 8) = 8 − 𝑗𝑗2 (Ом)

Вычисляем модуль и аргумент

= 8,25 Ом  

𝑋𝑋^о 

𝑋𝑋 = 𝑋𝑋_𝐿𝐿 − 𝑋𝑋_𝐶𝐶;        𝜑𝜑 = 𝑎𝑎𝑎𝑎𝑎𝑎𝑡𝑡𝑎𝑎 _𝑅𝑅 = −𝑎𝑎𝑎𝑎𝑎𝑎𝑡𝑡𝑎𝑎

Записываем в показательной форме

𝑍𝑍 = 𝑍𝑍𝑒𝑒𝑗𝑗𝜑𝜑 = 8,25𝑒𝑒−𝑗𝑗14о 

2.     Определяем комплекс тока в цепи по закону Ома:

𝐼𝐼̇ = 𝑈𝑈𝑍𝑍̇ = 𝑍𝑍𝑒𝑒𝑈𝑈𝑒𝑒⁻𝑗𝑗^𝑗𝑗140оо = 8,2580𝑒𝑒−𝑗𝑗0𝑗𝑗14о о = 9,7𝑒𝑒𝑗𝑗14о 

𝑒𝑒

3.     Определяем комплексы напряжений:

  𝑈𝑈̇_𝑅𝑅 = 𝐼𝐼𝑅𝑅̇ = 9,7𝑒𝑒^𝑗𝑗14⁰ ∙ 8 = 77,6𝑒𝑒𝑗𝑗14⁰В 

^𝑗𝑗90^о  jX_L = 𝑋𝑋_𝐿𝐿𝑒𝑒

𝑈𝑈̇_𝐿𝐿 = 𝑗𝑗𝑋𝑋_𝐿𝐿 ∙ 𝐼𝐼̇ = 9,7𝑒𝑒^𝐽𝐽14о ∙ 6𝑒𝑒𝑗𝑗90о = 58,2е𝑗𝑗104° В

^−𝑗𝑗90^о 

−𝑗𝑗𝑋𝑋_𝐶𝐶 = 𝑋𝑋_𝐶𝐶𝑒𝑒

𝑈𝑈̇_𝐶𝐶 = −𝑗𝑗𝑋𝑋𝐶𝐶 ∙ 𝐼𝐼̇ = 𝐼𝐼𝑒𝑒𝑗𝑗14о ∙ 𝑋𝑋𝐶𝐶𝑒𝑒−𝑗𝑗90о = 9,7𝑒𝑒𝑗𝑗14о ∙ 8𝑒𝑒−𝑗𝑗900 = 77,6𝑒𝑒−𝑗𝑗760В 

4.Для построения векторной диаграммы выбираем масштаб, определяем длины векторов:

M_I = 2 А/см,    М_U = 20 В/см,   l_UR =3,9 см,  l_UL= 2,9 см,  l_UC = 3,9 см

                                                             ̇

                                                                           ̇

                                               ̇

                                                                     ̇

̇

Контрольные вопросы

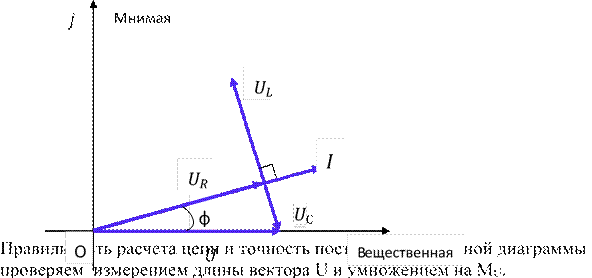1.     Какие формы комплексных чисел вы знаете?

2.     Какая форма комплексного числа используется при сложении, умножении, делении.

3.     Что такое аргумент и модуль.

4.     Построить треугольник сопротивлений.

Содержание отчета

1.     Тема, цель, задание

2.     Схема, расчеты, векторная диаграмма.

3.     Контрольные вопросы и ответы.