Практическое занятие.  Решение производственных задач с помощью электронных таблиц

Цель работы: изучить приемы решения систем уравнений с помощью электронных таблиц для решения производственных задач

Методические указания:

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ НАДСТРОЙКИ "ПОИСК РЕШЕНИЯ"

"Поиск решения" — это надстройка для Microsoft Excel, которую можно использовать для анализа "что если". С ее помощью можно найти оптимальное значение (максимум или минимум) формулы, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка "Поиск решения" работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка "Поиск решения" изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.

Проще говоря, с помощью надстройки "Поиск решения" можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.

Алгоритм решения системы уравнений, используя Поиск решения

1.     Преобразовать систему уравнений, если это необходимо

2.     Записать исходные данные

3.     В отдельных ячейках записать уравнения, используя правило записи арифметических выражений.

4.     Выбрать команду Поиск решения.

5.     Установить целевую ячейку - ту ячейку, в которой содержится формула, и задать значение, равное значению правой части первого уравнения

6.     В поле «Изменяя ячейки переменных» указать ячейки, в которых будем размещать ответ

7.     Ввести ограничение по уравнению 2 (значение правой части).

8.     Решить систему уравнений, щелкнув кнопкой Найти решение

Пример вычисления с помощью надстройки «Поиск решения»

В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).

1. 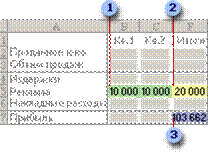  Ячейки переменных

2.   Ячейка с ограничениями

3.   Целевая ячейка

После выполнения процедуры получены следующие значения.

Решение уравнений методом Подбора параметров EXCEL

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

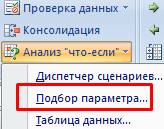Путь к команде: «Данные» - «Работа с данными» -

«Анализ «что-если»» - «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения

х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

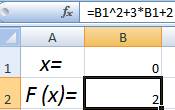Введем в ячейку В2 формулу для нахождения значения функции.

В качестве аргумента применим ссылку на ячейку В1.

Открываем  меню  инструмента  «Подбор  параметра».  В  графе

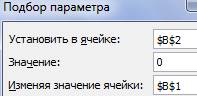«Установить в ячейку» - ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» - В1. Здесь должен отобразиться отобранный параметр.

После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

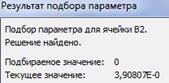
Для  подбора  параметра  программа  использует  циклический  процесс.

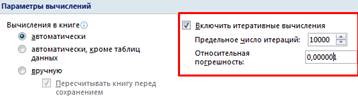Чтобы изменить число итераций и погрешность, нужно зайти в параметры   Excel.   На   вкладке

«Формулы» установить предельное количество итераций, относительную

погрешность. Поставить галочку «включить итеративные вычисления».

АЛГОРИТМ РЕШЕНИЯ СИСТЕМЫ ГРАФИЧЕСКИМ СПОСОБОМ

1.    Преобразовать систему уравнений (выразить переменную y из каждого уравнения), если это необходимо.

2.   Задать начальные значения для х

3.   Найти значение первой функции при заданных х

4.   Найти значение второй функции при тех же х

5.   Выделить блок с данными и построить графики функций (y), используя точечный тип диаграммы

6.   Решение системы - точка пересечения графиков функций.

7.     Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.

РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ МАТРИЧНЫМ МЕТОДОМ

Пусть дана система линейных уравнений (1). Матричный способ решения систем линейных уравнений используется в тех случаях, когда число уравнений равно числу переменных.

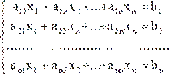(1)

Введем обозначения. Пусть А – матрица коэффициентов при переменных, B – вектор свободных членов, X – вектор значений переменных. Тогда X = A^-1 × B, где А^-1 – матрица, обратная А. Причем обратная матрица А^-1 существует, если определитель матрицы А не равен 0. Произведение исходной матрицы А и обратной А^-1 должно быть равно единичной матрице:

А^-1А=АА^-1=Е.

Ход работы:

ЗАДАНИЕ   1.   Примените   метод   поиска   решений   EXCEL   для                     решения следующей задачи:

Постановка задачи:

ООО «ПромДеталь» выпускает печатные платы трех видов: Однослойные, Многослойные (до 30 слоёв) и Светодиодные платы на металлическом основании. На производство плат 1-го вида рабочий тратит 36 часов, 2-го вида – 60 часов, 3-го вида – 72 часа. При реализации плат 1-го вида предприятие получает 560 руб, 2-го вида – 1260 руб., 3-го вида – 2130 руб. Компания должна выпустить не менее 100 штук плат 1-го вида, не менее 200 плат 2-го вида и не менее 150 штук 3-го типа.

Какое оптимальное количество плат каждого вида надо выпустить для получения наибольшей прибыли, если фонд рабочего времени составляет 30000 человеко-часов.

Математическая модель:

Обозначим Х₁, Х₂ и Х₃ – количество плат 1-го, 2-го и 3-го видов соответственно в оптимальном плане производства.

560Х₁+1260Х₂ +2130Х₃ ®  max  – целевая функция;

36Х₁+60Х₂ +72Х₃   £                              30000 Х₁ ³ 100

Х₂ ³ 200                                                  условия ограничения

Х₃ ³ 150

Х₁, Х₂, Х₃ - целые числа.

Технология выполнения задания:

1.     Сохраните файл под именем ПрСистемы-ФИО и переименуйте лист в

Задание1.

2.    

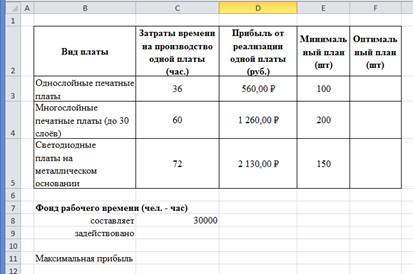3.     Вычислите значения «Задействовано» и «Максимальная прибыль» по формулам:

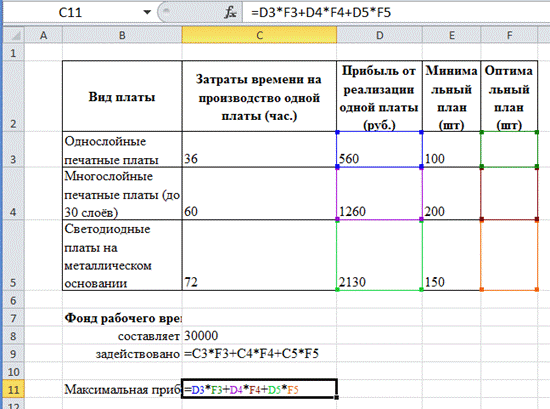4.     Запустите   надстройку   «Поиск  решения»   и   установите                   следующие параметры:

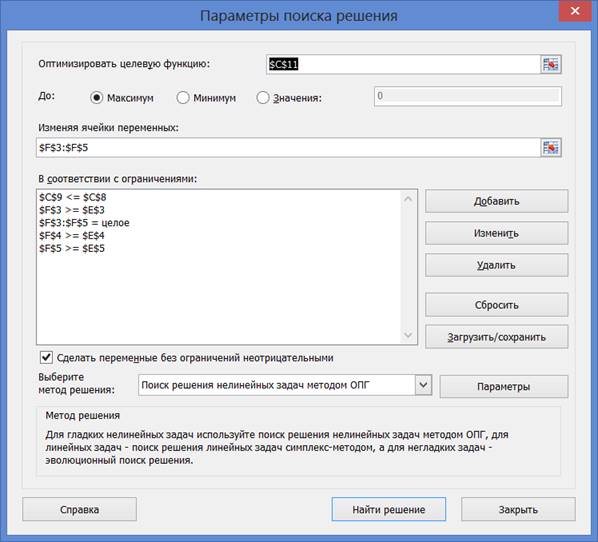
Нажмите Найти решение. Проверьте полученный результат:

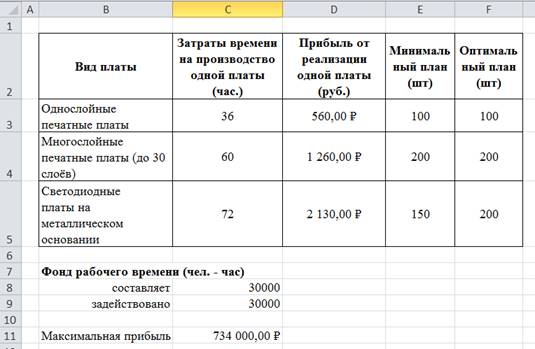Задание 2. Решите систему нелинейных уравнений графически. Постановка задачи

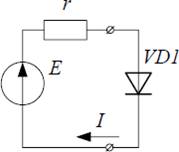
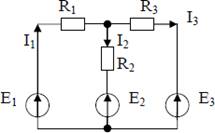
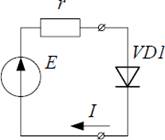
Пусть имеется генератор постоянного тока с ЭДС E и внутренним сопротивлением r (см. рис.1). К генератору подключен идеальный диод VD1. По цепи протекает ток I.

Рис. 1

Имеются следующие исходные данные:

·        ЭСД E = 1 В;

·        сопротивление r = 1 Ом;

·        температура диода T = 300 К;

·        обратный ток диода I0 = 10·10^-18 А.

Требуется  графическим  способом определить напряжение и мощность на диоде, ток в цепи.

Математическая модель:

Согласно второму закону Кирхгофа, ЭДС генератора E уравновешивается падением напряжения на сопротивлении r и напряжением на диоде VD1:

или                                         (3.1)

Вольт-амперная характеристика диода описывается уравнением    

(3.2), где I0 – тепловой (обратный) ток p–n-перехода; U – напряжение, приложенное к p–n-переходу;

q=1.6•10^-19 Кл - заряд электрона;

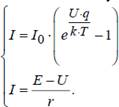k =1.38 •10^-23       – постоянная Больцмана;

T – температура p–n-перехода.

С   учётом   (3.1)   и   (3.2)   составим   систему     нелинейных уравнений

Подставим численные значения из условий задачи:

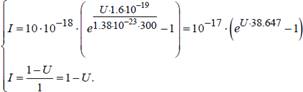(3.4)

Численное решение задачи в Excel

Графическим решением системы из двух уравнений (3.5) является точка пересечения прямой и экспоненты. Введём две функции от переменной U:

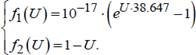(3.5)

Ход выполнения задания:

Переменная U изменяется в пределах от 0.9 до 0.97 В с шагом 0.005 В.

1)    Введите в ячейки А1, В1 и С1 названия столбцов (см.образец)

2)     Введите в ячейку А2 начальное значение переменной 0,9; в ячейку А3 введите 0,905. Для ввода интервала переменных выделите массив ячеек А2– А3 и протяните мышкой левый нижний угол массива до конечного значения 0,97 (ячейка А16)

3)   

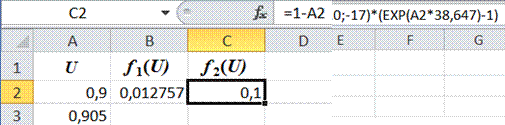4) 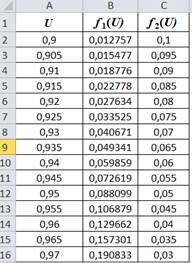   Скопируйте формулы до последнего значения U (ячейки В16 и С16)

5)     Выделите массив ячеек A2–C16, выберите Вставка - Диаграмма, тип Точечная с гладкими кривыми и маркерами. Оформите диаграмму (см. образец): проставьте линии сетки по вертикали и горизонтали, измените диапазоны значений переменных по вертикали и горизонтали, подписи осей, легенду. Получим график функций f1(U) и f₂(U)

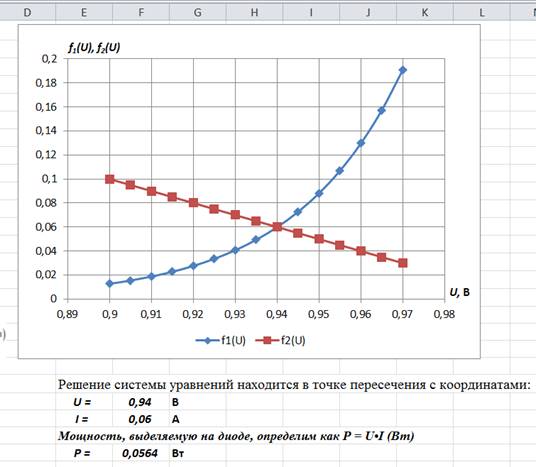
6)     Т.к. решение системы уравнений находится в точке пересечения с координатами U = 0.94 В и I = 0.06 А (занесите данные полученные значения в отдельные ячейки Excel, см. образец выше). И найдите мощность, выделяемую на диоде, которая определяется по формуле P = U • I (Вт).

Задание 3. Выполните расчёт цепи постоянного тока методом обратной матрицы

Пусть дана электрическая цепь (см. рис.2), состоящая из трёх ветвей. Известны величины ЭДС источников:

E1 = 10 В , E2 = 5 В, E3 = 3 В

и сопротивлений в каждой ветви:

R1 = 1 Ом , R2 = 2 Ом , R3 = 4 Ом .

Рис.2

Необходимо определить токи, протекающие в каждой ветви.

Математическая модель:

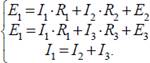Для трёх неизвестных токов I₁, I₂, I₃ составим систему из трёх уравнений, согласно первому и второму закону Кирхгофа:

(1)

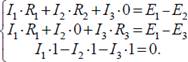Преобразуем её следующим образом

(2)

Подставим в (2) численные данные и получим матрицу коэффициентов

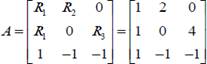(3)

и матрицу свободных членов

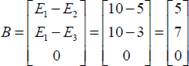(4)

Решение системы уравнений (1) найдём как

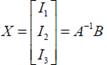       (5)

Ход выполнения задания:

1)    

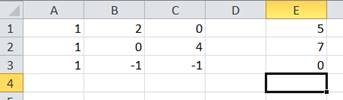2)     Обратную матрицу от матрицы коэффициентов разместите в массиве ячеек

G1–I3 – для этого выделите его, затем вызовите мастер функций (кнопка

) или меню Формулы и в категории Математические выберите МОБР

3)    В окне Аргументы функции введите адрес источника данных A1:C3

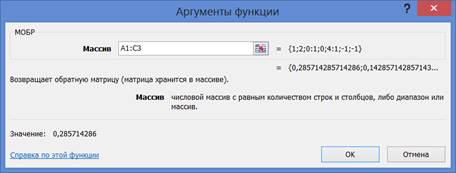         и     для                   создания массива             значений                  нажмите (не                   клавишу     ОК),                        а                    клавиши

<CTRL>+<SHIFT>+<ENTER>. В результате получим обратную матрицу

(обратите внимание как Excel сформировал формулу для массива):

4)     Выполните умножение обратной матрицы, размещённую в ячейках G1–I3, на матрицу свободных членов, размещённую в ячейках E1–E3. Для этого выделите массив ячеек результата F5–F7, вызовем с помощью мастера функций функцию МУМНОЖ из категории Математические

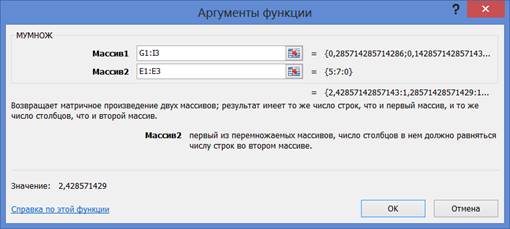5)     В опции Аргументы массива введите адрес первого массива G1–I3 и адрес второго    массива    E1–E3,    а    затем    нажмите    клавиши

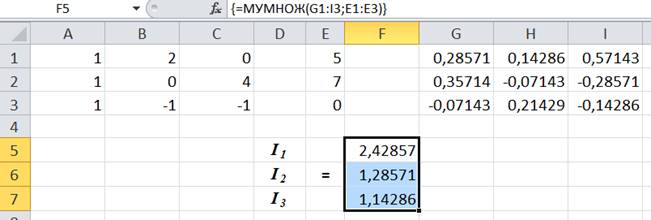Полученные результат                                 , размещённый в ячейках F5–F7, является истинным, так как выполняется первый закон Кирхгофа – третье уравнение системы (1).

Проверку полученного результата можно выполнить и по первому, и по второму уравнениям системы (1).

Задание 4 (выполнение аналогично заданию 2). Решите систему нелинейных уравнений графически.

Постановка задачи

Пусть имеется генератор постоянного тока с ЭДС E и внутренним сопротивлением r (см. рис.1). К генератору подключен идеальный диод VD1. По цепи протекает ток I.

Рис. 1

Имеются следующие исходные данные:

·        ЭСД E = 2,1 В;

·        сопротивление r = 0,9 Ом;

·        температура диода T = 300 К;

·        обратный ток диода I0 = 10·10^-18 А.

Требуется  графическим  способом определить напряжение и мощность на диоде, ток в цепи.

В   графике   при   необходимости   один   из   рядов  можно   расположить   на вспомогательной оси

Ответ записать в отдельных ячейках рядом с графиком (см. образец задания 2).

Задание 5 (выполнение аналогично заданию 3). Выполните расчёт цепи постоянного тока методом обратной матрицы

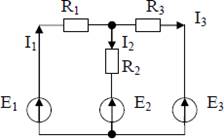Пусть дана электрическая цепь (см. рис.2), состоящая из трёх ветвей. Известны величины ЭДС источников:

E1 = 12 В , E2 = 6 В, E3 = 4 В

и сопротивлений в каждой ветви:

R1 = 2 Ом , R2 = 1 Ом , R3 = 4 Ом .

Рис.2 Необходимо определить токи, протекающие в каждой ветви. Ключ к выполнению задания:

1)     постройте исходную матрицу (матрицу коэффициентов по формуле 3 задания 3)

2)     определите и постройте матрицу свободных членов (по формуле 4 задания 3)

3)    вычислите обратную матрицу от матрицы коэффициентов

4)    выполните умножение обратной матрицы на матрицу свободных членов

5)    выполните проверку уравнению системы, т.е.

ЛИТЕРАТУРА

1.   Макенова Н. А. Решебник по электротехнике: учебное пособие / Н. А. Макенова, Т. Е. Хохлова, Томский политехнический университет. – Томск : Изд-во Томского политехнического университета, 2015. – 165 с. – Текст : электронный

2.   Михеева Е. В. Практикум по информационным технологиям в профессиональной деятельности: учеб. пособие для студ. учреждений сред. проф. образования. - 13-е изд., испр. – М. : Академия, 2013. – 256 с.

3.   Холи Р., Холи Д. Excel. Трюки. — СПб.: Питер, 2005. — 287 с.: ил. – Текст : электронный

Интернет-ресурсы:

1.     MS Excel для новичков и профессионалов - [Сайт]. URL: https://excel2.ru/ (дата обращения 27.12.2018)

2.     Работа с таблицами ExcelTABLE - [Сайт]. URL: https://exceltable.com/uroki-  excel/  (дата обращения 27.12.2018)

3.     Скачано с www.znanio.ru