Решение систем и совокупностей неравенств_Методические рекомендации к уроку №6 (1)

Методические рекомендации к проведению урока

Тема урока: Решение систем и совокупностей неравенств

Тип урока: Урок закрепления знаний

Цели обучения:

8.2.2.11

решать системы и совокупности двух квадратных неравенств;

Цели урока:

•         решать системы и совокупности из двух квадратных неравенств с дополнительным условием;

•         находить область определения функции и область допустимых значений алгебраического выражения через решение системы неравенств.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Полезно знать.

3.    Повторение.

4.    Углубление изучаемой темы.

5.    Индивидуальная работа.

6.    Самостоятельная работа.

7.    Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

Понятие система – совокупность.

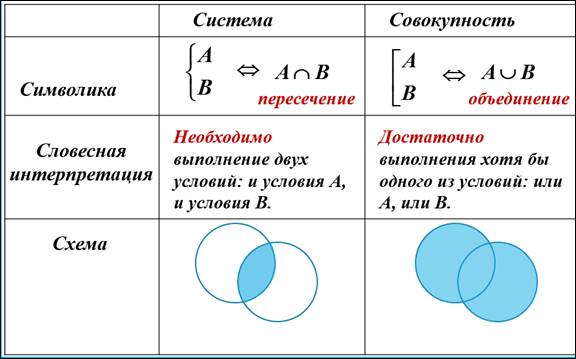
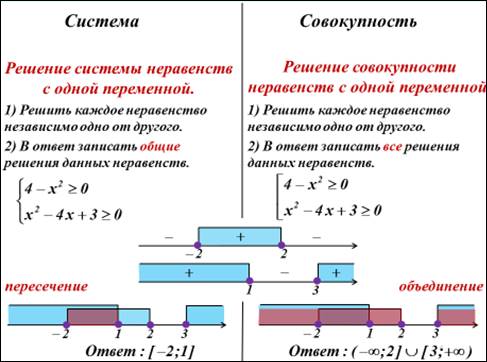
Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Задания, оформленные отдельным приложением, несмотря на то, что они включены в презентацию, необходимо предоставить учащимся обязательно в распечатанном виде. А имеющиеся слайды использовать при обсуждении с классом и при оценивании выполненной работы. Это поможет свести к минимуму использование интерактивной доски.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при изучении новой темы, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Часто при решении систем нелинейных неравенств учащиеся допускают такую ошибку: приравнивают к нулю левые части неравенств, находят корни и все корни наносят на одну ось, что является не верным. Очень важно не допускать и при выявлении искоренять эту и другие возможные типичные ошибки учащихся.

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

Решите систему и совокупность неравенств, найдите, если возможно, наибольшее и/или наименьшее значения решения:

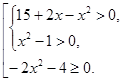
Продвинутый уровень

Решите систему и совокупность неравенств, найдите, если возможно, наибольшее и/или наименьшее значения решения:

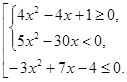
Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям будут полезны для организации самооценивания или взаимооценивания учащихся.

Ответы к приложению 1.

1. .          2. .              3..                 4..     

5. , наибольшего/наименьшего значения нет.         

6.  

Ответы к приложению 2.

1.      2. .

Критерии оценивания к каждому блоку заданий прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Н. Шыныбеков – 3-издание. – Алматы: «Атамұра», 2012. 288 с.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Е. Абылкасымова – Алматы: «Мектеп», 2008. 144 с.

Алгебра. 9  класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 21-е изд., испр. — М. : Мнемозина,

2014.

https://www.yaklass.ru/p/algebra/9-klass/neravenstva-i-sistemy-neravenstv-9125/sistemy-ratcionalnykh-neravenstv-9130/re-593f2460-36e5-4a0c-a154-3472fdc8be22

Скачано с www.znanio.ru