Решение систем и совокупностей неравенств_Методические рекомендации к уроку №6 (2)

Методические рекомендации к проведению урока

Тема урока: Решение систем и совокупностей неравенств

Тип урока: Урок закрепления знаний

Цели обучения:

8.2.2.11

решать системы и совокупности двух квадратных неравенств;

Цели урока:

Учащиеся

• составляют систему или совокупность неравенств;
• решают квадратные неравенства;
• решают системы неравенств;
• решают совокупности неравенств.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Повторение.

3.    Решение задачи на составление и решение двойного неравенства.

4.    Решение систем и совокупностей, в составе которых имеются квадратные и дробно-рациональные неравенства.

5.    Решение совокупности систем неравенств.

6.    Самостоятельная работа.

7.    Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

Значение переменной, при котором хотя бы одно из неравенств совокупности обращается в верное числовое неравенство, называется решением совокупности неравенств. Множество решений совокупности неравенств есть объединение множеств решений, входящих в нее неравенств.

Совокупность неравенств записывается с помощью квадратной скобки. 

Для того, чтобы найти решение совокупности неравенств необходимо

1)      отдельно решить каждое из неравенств;

2)      найти объединение решений этих неравенств.

Учитель обращает внимание учащихся на то, что при решении систем неравенств определяется пересечение решений неравенств, а при решении совокупностей неравенств – объединение.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при изучении новой темы, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

Решите системы и совокупности неравенств:

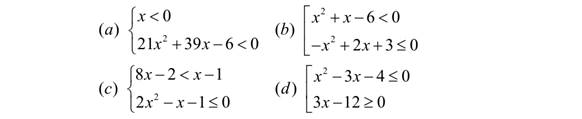
Продвинутый уровень

Решите совокупности систем неравенств:

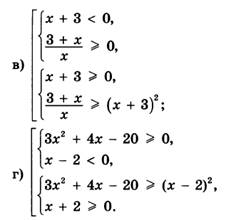
Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям будут полезны для организации самооценивания или взаимооценивания учащихся.

Ответы к приложению 1.

№1.

№2. а) все целые числа кроме 2; б) все целые числа кроме 1, 2, 3, 4, 5, 6, 7; в) все целые числа.

№3.

Критерии оценивания к каждому блоку заданий прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Мордкович А.Г., Николаев Н.П. Алгебра 9 класс, учебник для общеобразовательных учреждений. – М.: Мнемозима, 2008.

Мордкович А.Г., Николаев Н.П. Алгебра 9 класс, задачник для общеобразовательных учреждений. – М.: Мнемозима, 2008.

Звавич Л.И., Рязановский А.Р., Семенов В.П. Алгебра 9 класс, задачник для общеобразовательных учреждений.  – М.: Мнемозима, 2008.

http://interneturok.ru/ru/school/algebra/9-klass/sistemy-racionalnyh-neravenstv/sistemy-iz-lineynyh-i-kvadratnyh-neravenstv

Скачано с www.znanio.ru