Решение стереометрических задач .

Решение задач по стреометрии с разбором для подготовки к егэ

профильная математика.

Учитель МБОУ «Шалинская СОШ №90»

Пустовалова Л.М.

1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁   известны длины рёбер:AB=6, AD=10,  AA₁ =16. На рёбрах AA₁ и BB₁  отмечены точки E и F соответственно, причём

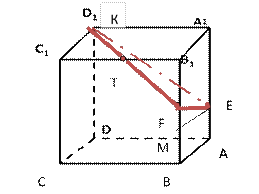
A₁ E:EA=5:3 и B₁F:FB=5:11. Точка T – середина ребра B₁ C₁. а) Докажите, что плоскость EFT проходит через точку D₁;   б) Найдите площадь сечения параллелепипеда плоскостью EFT. Решение.

а) Предположим, плоскость EFT пересекает А₁D₁  в точке К.

 ТF II КЕ так как это линии пересечения параллельных плоскостей плоскостью EFT.  Рассмотрим треугольники КЕА₁ и TFВ₁ (прямоугольные) и угол А₁ЕК равен углу ТFВ₁

(ТF II КЕ, ЕА₁ II FВ₁ ).  ∆КЕА₁ подобен ∆TFВ₁. = 10, FВ.

 ТF :  КЕ  = FВ₁ :  ЕА₁ = 5 : 10 = 1: 2 ,  следовательно ТF :  КЕ = В₁Т : А₁ К = 1 : 2. В₁Т = 10: 2 = 5 (Т – середина B₁ C₁ ) , следовательно  А₁ К = 10, по условию А₁D₁ = 10,  К = D₁, плоскость EFT пересекает А₁D₁  в точке D₁.

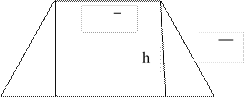
б) Сечение параллелепипеда плоскостью EFT – трапеция EFT D₁.

   T D₁ находим из ∆ C₁D₁Т по теореме Пифагора.   T D

EF находим из ∆ЕМF (проведем ЕМ II АВ, ЕА = ВМ = 16-10 = 6,  МF = ВВ₁ - FВ₁ – МВ

= 16 - 5 – 6 = 5). ∆ЕМF – прямоугольный (угол ЕМF прямой),  ЕF

, трапеция EFT D₁ равнобедренная.   S + Е D₁) h.    h     =

 .

ТF  , Е D₁ = 10      S   + Е D₁) = 97,5. 

Ответ: 97,5 кв.ед

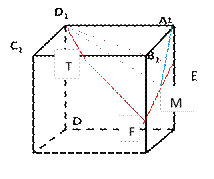
2. На ребре AA₁прямоугольного параллелепипеда ABCDA₁B₁C₁D₁  взята точка E так, что A₁ E:EA =1:2, на ребре BB₁ – точка F так, что B₁F:FB =1:5, а точка Т – середина ребра  B₁ C₁. Известно, что AB=2, AD=6, AA₁=6.

 а) Докажите, что плоскость EFT проходит через вершину D₁.

 б) Найдите угол между плоскостью EFT и плоскостью AA₁B₁.

а) Предположим, плоскость EFT пересекает А₁D₁  в точке К.

 ТF II КЕ так как это линии пересечения параллельных плоскостей плоскостью EFT.  Рассмотрим треугольники КЕА₁ и TFВ₁ (прямоугольные) и угол А₁ЕК равен углу ТFВ₁ (ТF II КЕ, ЕА₁ II FВ₁ ).  

∆КЕА₁ подобен ∆TFВ AA ВВ₁ = 1.

 ТF :  КЕ  = FВ₁ :  ЕА₁ = 1 : 2,  следовательно ТF :  КЕ = В₁Т : А₁ К = 1 : 2. В₁Т = 6: 2 = 3 (Т – середина B₁ C₁ ) , следовательно  А₁ К = 6, по условию А₁D₁ = 6,  К = D₁, плоскость EFT пересекает А₁D₁  в точке D₁.

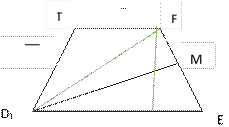
б)  Пусть угол между плоскостью EFT и плоскостью AA₁B₁ равен  Х – линейный угол двугранного угла  между плоскостями (EFT) и (AA₁B₁). EF – линия пересечения (EFT) и (AA₁B₁). Проведем в (EFT) D₁М┴ EF. А₁ D₁ ┴ (AA₁B₁) , следорвательно А₁ D₁ ┴ А₁М. D₁М – наклонная к (AA₁B₁), А₁М- проекция

D₁М, так как А₁ D₁ ┴ А₁М, по теореме о трех перпендикулярах EF ┴А₁М, следовательно  

Х - լА₁М D₁ sinХ = А₁ D₁ : М D₁ , А₁ D₁= 6,  EF  . 

М D₁ – высота в треугольнике FD₁M, площадь ∆ FD.

 S_трап ) h,       h .

 S_треуг  М D₁,  М D₁ = 6 : ,  sinХ = А₁ D₁ : М D

,      Ответ: Х =   

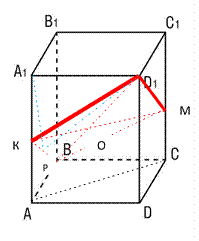
3.     Сечением прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ плоскостью  , содержащей прямую BD₁ и параллельной прямой AC, является ромб. а) Докажите, что грань ABCD – квадрат. б) Найдите угол между плоскостями  и BCC₁, если AA₁=10, AB=12.

Решение.  а) Проведем МК II АС. Через середину В D₁ точку О → точки К, М – середины боковых ребер и АК = МС = 5, КВ = ВМ (сечение параллелепипеда плоскость -ромб).

∆АКВ = ∆ВМС (прямоугольные, АК = МС = 5, КВ = ВМ) по катету и гипотенузе , следовательно АВ = ВС.

 Следовательно смежные стороны прямоугольника АВСD равны → АВСD – квадрат. б) обозначим угол между плоскостями  и BCC₁ – Х.

Х – линейный угол между плоскостями  и BCC₁. Проведем высоту в ромбе D₁Р к стороне КВ, так как КВ – линия пересечения  и BCC₁. Рассмотрим ∆Р А₁ D₁ прямоугольный: 

 А₁ D_1┴ А₁ Р, так как плоскости АВВ₁ и АА₁ D₁ перпендикулярны. А₁ Р – проекция наклонной D₁Р и D₁Р┴КВ →по теореме о трех перпендикулярах КВ ┴ А₁ Р →լ А₁ РD₁ – линейный угол линейный угол между плоскостями  и BCC₁ → լ А₁ РD₁ =Х.

- высота ромба, проведенная к стороне КВ.

S_ромба = КВ• D Р =  КМ • В D₁ → D Р =(  КМ • В D₁) : КВ

КМ = АС = 12, В D₁ =  = 2,  КВ =       = 13, D) : 13 =, 

 → Х =  . 

Ответ: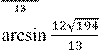   

Задачи для самостоятельного разбора.

1. В прямоугольном параллелепипеде ABCDA₁B₁С₁D₁ известны длины рёбер:

AB=2, AD=6, AA₁ =10.

 На рёбрах AA₁ и BB₁ отмечены точки E и F соответственно, причём A₁ E:EA=3:2 и B 1F:FB=3:7. Точка T – середина ребра B₁ C₁. а) Докажите, что плоскость EFT проходит через точку D₁. б) Найдите площадь сечения параллелепипеда плоскостью EFT.

2.На ребре AA₁прямоугольного параллелепипеда ABCDA₁B₁C₁D₁  взята точка E так, что A₁ E:EA =2:3, на ребре BB₁ – точка F так, что B₁F:FB =1:4, а точка Т – середина ребра  B₁ C₁. Известно, что AB= 6 , AD= 4, AA₁= 10.

 а) Докажите, что плоскость EFT проходит через вершину D₁.

 б) Найдите угол между плоскостью EFT и плоскостью AA₁B₁.

3. Сечением прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ плоскостью  , содержащей прямую BD₁ и параллельной прямой AC, является ромб. а) Докажите, что грань ABCD – квадрат. б) Найдите угол между плоскостями  и BCC₁, если AA₁=16, AB=15.