Решение стереометрических задач методами аналитической геометрии

Муниципальное казенное общеобразовательное учреждение

«Барановская средняя общеобразовательная школа»

 

 

 

 

 

 

 

«Решение стереометрических задач методами аналитической геометрии».

(занятие элективного курса)

 

 

подготовила Амерева Е. Э.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2017

Занятие элективного курса  в 11 классе  «Решение стереометрических задач методами аналитической геометрии».

(математический квест)

 

Цель: создание условий для формирования навыка решения стереометрических задач различными способами.

Задачи:

          ·           способствовать развитию наглядно-образного мышления, внимания;

          ·           развивать умение высказывать собственные суждения, аргументировать свою точку зрения;

          ·           воспитывать умение  планировать свою работу, искать рациональные пути решения задач.

ТСО: компьютер с выходом в сеть Интернет,  мультимедийный проектор, презентация к уроку

Комментарии: на уроке рассматриваются задачи ЕГЭ типа «№14», можно использовать данный материал для организации итогового повторения.

Актуальность:  Часто стереометрические задачи «пугают» выпускников только самим наличием трех измерений. Если у школьника имеются серьезные проблемы с пониманием определений, с чтением или построением сложного стереометрического рисунка, если ему никак не удается подобрать необходимые дополнительные построения, то можно построить работу по №14 на векторах и координатах. Применение аналитической геометрии (и знание небольшого числа формул) часто способно существенно облегчить решение задачи.

Ход урока

I. Организационный момент.

Квест — это увлекательная «живая» игра для команды из нескольких человек, в специально оборудованном для этого помещении. Участникам предлагается выполнить определенное задание, ограниченное по времени. Здесь вам не обойтись без смекалки, логического мышления, эрудиции, а также умения взаимодействовать с товарищами.

II. Актуализация знаний.

В задаче 14 рассматриваются многогранники, на основе которых, как правило, нужно найти одну из следующих величин:

1. Угол между скрещивающимися прямыми — это угол между двумя прямыми, которые пересекаются в одной точке и параллельны данным прямым.

2. Угол между прямой и плоскостью — это угол между самой прямой и ее проекцией на данную плоскость.

3. Угол между двумя плоскостями — это угол между прямыми, которые лежат в данных плоскостях и перпендикулярны линии пересечения этих плоскостей.

Традиционный метод решения

В школьном курсе стереометрии упор делается на дополнительные построения, которые позволяют выделить искомый угол, а затем рассчитать его величину.

Здесь уместно вспомнить задачи на построение сечений многогранников, которые рассматриваются в 10 классе и у многих вызывают трудности. Существование формального алгоритма для таких построений совершенно не облегчает задачу, поскольку каждый случай достаточно уникален, а любая систематизация лишь усложняют процесс.

Именно поэтому задача 14 оценивается в два балла. Первый балл дается за правильные построения, а второй — за правильные вычисления и собственно ответ.

Преимущества традиционного решения:

1. Высокая наглядность дополнительных построений, которые подробно изучаются на уроках геометрии в 10-11 классах;

2. При правильном подходе значительно сокращается объем вычислений.

Недостатки:

1. Необходимо знать большое количество формул из стереометрии и планиметрии;

2. Дополнительные построения каждый раз приходится придумывать «с нуля». И это может оказаться серьезной проблемой даже для хорошо подготовленных учеников.

Впрочем, если у вас хорошее стереометрическое воображение, проблем с дополнительными построениями не возникнет. Остальным предлагаю отказаться от традиционного геометрического метода и рассмотреть более эффективный алгебраический подход. Итак, поехали!

 

III. Тренировочные упражнения.

Класс делится на две группы

3.1. Повторение теории:

1)      - устно в режиме он-лайн (https://learningapps.org/display?v=p77zekd9a17)

 

2)      - координатный метод (некоторые формулы)

Прямоугольная система координат в пространстве

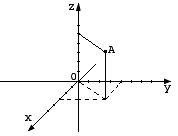
Рис.1

Ох, Оу, Оz - оси абсцисс, ординат и аппликат. Координаты точки А записываются так: А (х; у; z) (см. Рис.1).

Координатный метод

Координатный метод позволяет рассматривать множество самых трудных задач на вычисление всех видов углов (между прямыми, между прямой и плоскостью, между плоскостями) и любых расстояний (от точки до плоскости, между параллельными плоскостями, между скрещивающимися прямыми).

· Необходимо выбрать систему координат, исходя из удобства расположения фигуры. Найти координаты нужных точек.

· Решить задачу, используя основные формулы метода координат.

Опорные формулы:

    (1)

 (2)

   (3)

     (4)

Расстояние от точки M(x0,y0) до прямой, заданной уравнением

                           ,

 

 

3.2.

Задача 1. Разбирается учителем совместно с учениками

Приложение 1,

Приложение 2 сл1-2

 

3.3 Задачи№ 2,3 группы решают указанным способом,.

Заслушивается отчет каждой группы по решению

 

 

Задача 2. В единичном кубе ABCDA₁B₁C₁D₁ найти расстояние от точки D₁ до прямой PQ, где P и Q – середины соответственно ребер A₁B₁ и BC.

 

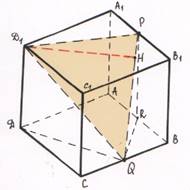Поэтапно-вычислительный метод

Пусть D₁H  PQ, где HPQ, R -  середина ребра AB. Найдем D₁H.

ΔBRQ -  прямоугольный,  QR=

ΔPQR -  прямоугольный, PQ =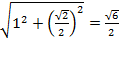

ΔDCQ - прямоугольный, DQ =

Δ D₁DQ- прямоугольный,  D₁Q =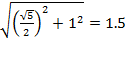

D₁P = DQ =

В треугольнике D₁PQ по теореме косинусов ; ;  .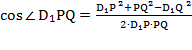

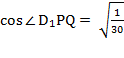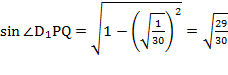D₁H= D₁P 

D₁H= = .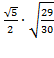

Ответ: .

 

 

 

 

 

 

Задача 2. В единичном кубе ABCDA₁B₁C₁D₁ найти расстояние от точки D₁ до прямой PQ, где P и Q – середины соответственно ребер A₁B₁ и BC.

 

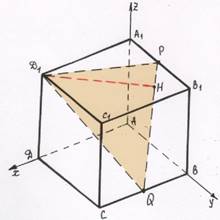Метод координат

 ПустьD₁QP =

Тогда из прямоугольного треугольника D₁QP

D₁ H = QD₁

Рассмотрим прямоугольную систему координат с началом в точке А.

Найдем координаты точек  P(0; 0.5; 1),

Q(0.5; 1;0), D₁(1;0;1), тогда

По формуле длины вектора

Используя формулу угла между векторами

,

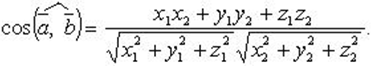получаем:

cos= =

 

=

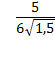
D₁ H = QD₁          D₁ H =

Ответ: .

 

Задача 3

Боковое ребро МА пирамиды МАВС перпендикулярно плоскости основания и равно 13, , АВ=39, АС=52. Найдите расстояние от вершины А до плоскости ВСМ.  

Поэтапно-вычислительный метод

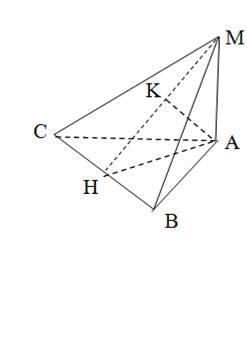
Если через точку А провести плоскость, перпендикулярную плоскости ВСМ, то перпендикуляр, проведенный через точку А к линии пересечения этих плоскостей, будет перпендикуляром и к плоскости ВСМ.

Пусть АН ВС , тогда по теореме о трех перпендикулярах МНВС. Следовательно, ВС  АМН и МВС АМН.

Проведем в плоскости АМН перпендикуляр АК к прямой МН. Тогда АК

ВСМ. Длина отрезка АК  равна расстоянию от точки А до плоскости ВСМ.

В треугольнике АВС

ВС=

 

, тогда АН =.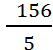

В треугольнике АМН

МН=

 

 АК= 12

 

 

 

ОТВЕТ: 12.

Координатный  метод

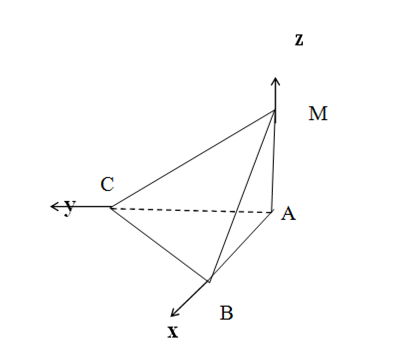
1. Введем систему координат и найдем координаты нужных точек.

 

А(0,0,0) В(39,0,0) С(0,52,0) М(0,0,13)

 

 

2. Напишем уравнение плоскости (ВМС) по трем точкам.

 

Ax+By+Cz+D=0

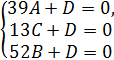
Пусть D= -13

Тогда уравнение плоскости: 4x+3y+12z-156=0

 

3. Найдем расстояние от точки А(0,0,0)до плоскости (ВМС) по соответствующей формуле:

 

 

 

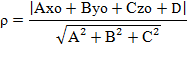
ОТВЕТ: 12.

 

3 4. Задачу 4 группы решают любым выбранным способом

В ходе отчета по решению задачи необходимо дать обоснование выбора решения.

Задача 4 Точка Е - середина ребра АА₁ куба ABCDA₁B₁C₁D₁ Найдите площадь сечения куба плоскостью C₁DE, если ребра куба равны 2.

 

 

Поэтапно-вычислительный метод

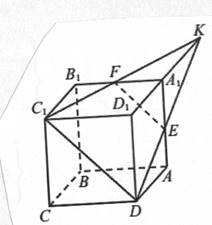
Решение

Прямая DE пересекает прямую А₁ D₁ в точке K.

Прямая С₁K пересекает ребро A₁B₁ в его середине – точке F.

C₁DEF – сечение куба плоскостью C₁DE.

В равнобедренном треугольнике C₁DK

и высота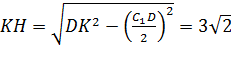

Поскольку EF – средняя линия треугольника C₁DK  , получаем:

 

 

 

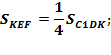
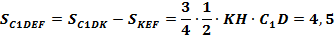
Ответ: 4,5

 

Координатный  метод

 

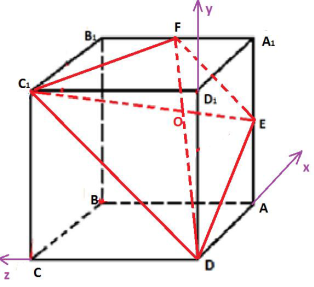
Решение:

Сечение куба - трапеция C₁ DEF, F- середина А₁ В₁;

Введём прямоугольную систему координат: D(0;0;0);  ОХ совпадает с лучом DA, OY с лучом DD₁, OZ с лучом DC.

Ребро куба 2.Тогда C₁(0;2;2), E(2;1;0), F(2;2;1)

 

Ответ: 4,5

Задача 5

В правильной шестиугольной пирамиде SABCDEF , стороны основания  которой равны 1, а боковые рёбра равны 2, точка K – середина ребра SD . Найти косинус угла между прямыми AS и FK .

 

Поэтапно-вычислительный метод

 

Ребро AS и точка K лежат в плоскости ASD , тогда средняя линия KO треугольника ASD будет параллельна AS и угол

(AS, FK)  (KO, FK).

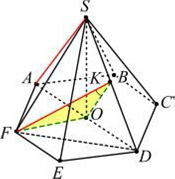
Точка O – центр основания пирамиды. Найдем угол FKO треугольника

FKO . Для этого найдем длины его сторон. Так как в основании пирамиды ле- жит правильный шестиугольник, то отрезок FO равен его стороне, то есть

FO =1.

Соответственно отрезок KO –средняя линия треугольника ASD и KO =

Найдем FK . Рассмотрим равнобедренный треугольник FSD , в котором

FS =SD = 2, а  FD =

 

Учитывая, что FK – медиана треугольника FSD получаем

 

 

=

 

 

Теперь из теоремы косинусов для треугольника FKO находим:

 

 

 

Ответ:

 

Задача 5

В правильной шестиугольной пирамиде SABCDEF , стороны основания  которой равны 1, а боковые рёбра равны 2, точка K – середина ребра SD . Найти косинус угла между прямыми AS и FK .

Координатный  метод

Введем прямоугольную систему координат, как указано на рисунке .

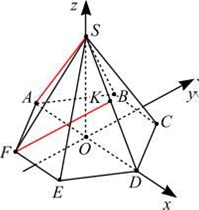
Так как пирамида правильная, то точка O – центр основания пирамиды и из

прямоугольного треугольника ASO получаем SO=

Тогда А(-1;0;0) , D(1;0;0) ,     F () , S(0; 0; ) .

 

Учитывая,что точка K – середина отрезка SD , получаем K (               ) .

Отсюда имеем

 

 {                }, FK {                },

 

Используя формулу, находим

 

 

 

 

 

cos((AS, FK))=

 

 

 

Ответ:

 

 

 

 

IV.Подведение итогов занятия.

Приложение (приз победителю)

Координаты вершин многогранников

 

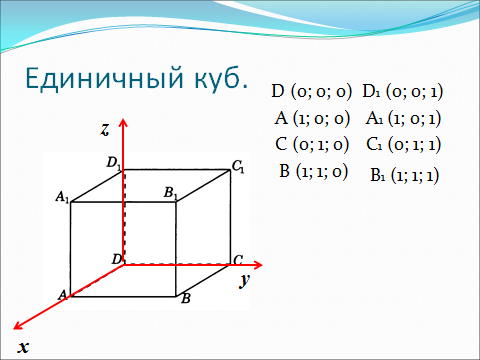
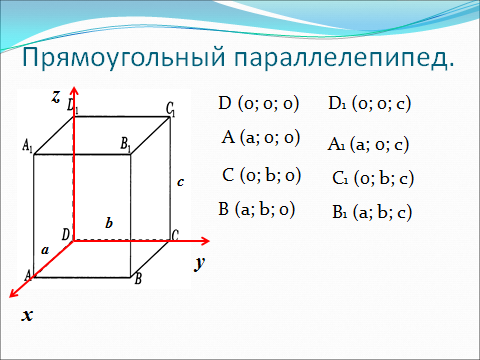
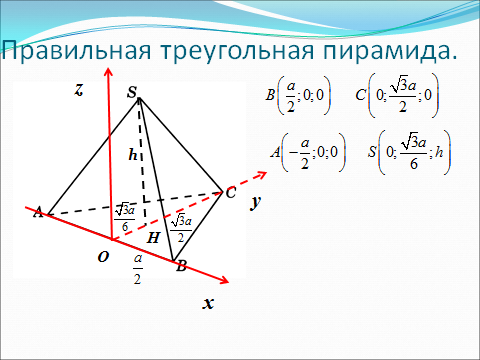
Метод координат в пространстве