РЕШЕНИЕ ЗАДАЧ

Решение задач

Цели: закрепить умение учащихся решать задачи с помощью систем уравнений; подготовить учащихся к контрольной работе.

Ход урока

I. Устная работа.

Придумайте задачу, для решения которой нужно составить систему уравнений:

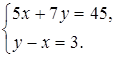
II. Формирование умений и навыков.

1. № 1107.

Решение:

Пусть первый автомат изготовлял в час х деталей, а второй – у деталей. Заполним таблицу:

Составим и решим систему уравнений:

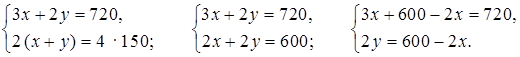
3х + 600 – 2х = 720;

х = 120;

2у = 600 – 2 · 120 = 360;

у = 180.

Ответ: 120 и 180 деталей.

2. № 1115.

Решение:

Пусть слиток золота весит х г, а слиток серебра весит у г. Согласно условию 9 слитков золота и 11 слитков серебра весят одинаково. Получим уравнение: 9х = 11у.

После того как поменяли местами один слиток золота с одним слитком серебра, на левой чаше оказалось 8 слитков золота и 1 слиток серебра, их общая масса равна (8х + у) г. На правой чаше стало 10 слитков серебра и 1 слиток золота, их общая масса равна (10у + х) г. По условию левая чаша на 13 г легче правой, значит, получим уравнение:

(10у + х) – (8х + у) = 13.

Составим и решим систему уравнений:

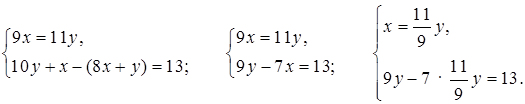
9y – y = 13;

81y – 77y = 117;

4у = 117;

у = 29,25;

х = ;

х = 35,75.

Ответ: 35,75 г и 29, 25 г.

3. № 1118.

Решение:

Пусть первая бригада по плану за месяц должна была изготовить х деталей, а вторая бригада – у деталей. По условию вместе они должны за месяц изготовить 680 деталей, то есть получим уравнение: х + у = 680.

Первая бригада, перевыполняя план, изготовила за месяц на 0,2х деталей больше, а вторая – на 0,15у деталей больше. По условию сверх плана было изготовлено 118 деталей, то есть получим уравнение:

0,2х + 0,15у = 118.

Составим и решим систему уравнений:

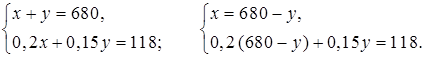
0,2 (680 – у) + 0,15у = 118;

136 – 0,2у + 0,15у = 118;

–0,05у = –18;

у = 360;

х = 680 – 360;

х = 320.

Ответ: 320 и 360 деталей.

Если останется время, можно предложить учащимся задачи повышенного уровня сложности.

4*. № 1120.

Решение:

Пусть на вклад «Депозитный» клиент положил х р., а на вклад «До востребования» – у р.

По условию всего клиент положил в банк 45000 р., то есть получим уравнение: х + у = 45000.

Доход от вклада «Депозитный» составил 9 %, то есть 0,09 х р., а от вклада «До востребования» 1 %, то есть 0,01у р. Общий доход клиента по условию равен 3410 р., значит, получим уравнение: 0,09х + 0,01у = 3410.

Составим и решим систему уравнений:

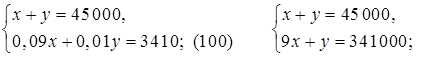
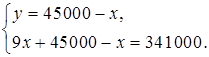
9х + 45000 – х = 341000;

8х = 296000;

х = 37000;

у = 45000 – 37000;

у = 8000.

Ответ: 37000 р. и 8000 р.

5*. № 1121.

Решение:

Пусть 10 %-ного раствора нужно взять х г, а 15 %-ного – у г.

Всего  нужно  получить  80 г  раствора,  то  есть  получим  уравнение:
х + у = 80.

В х г  10 %-ного  раствора  содержится  0,1х г соляной кислоты, а в у г 15 %-ного раствора – 0,15у г соляной кислоты. В результате получили 80 г 12 %-ного раствора, в нём соляной кислоты 80 · 0,12 = 9,6 г.

Получим уравнение: 0,1х + 0,15у = 9,6.

Составим и решим систему уравнений:

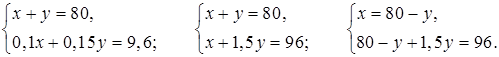
80 – у + 1,5у = 96;

0,5у = 16;

у = 32;

х = 80 – 32 ;

х = 48.

Ответ: 48 г и 32 г.

III. Итоги урока.

– Что называется решением системы уравнений с двумя переменными?

– Какие существуют способы решения систем уравнений? Опишите каждый из них.

– Как решить задачу с помощью системы уравнений?

Домашнее задание: № 1114; № 1116; № 1117.

Дополнительно: № 1122.