
Технологическая карта
Класс: 11
Тема урока:Решение заданий с параметром графическим методом.
Тип урока:Закрепление материала
Цель урока:закрепление умений и навыков решать задания с параметром графическим методом.
Задачи урока:
· Повторение навыков работы с модулем.
· Систематизация и обобщение знаний различных типахфункций.
· Подготовка к ЕГЭ.
· Развитие логического мышления, умений самостоятельно работать, навыков самоконтроля, умений говорить и слушать, интереса учащихся к предмету, их стремление глубже усвоить предмет.
· Воспитание отзывчивости, трудолюбия, аккуратности
План урока:
I. Организационный момент.
|
Дидактическая задача этапа |
Время |
Содержание деятельности учителя |
Условия получения положительного результата |
Форма работы |
Оборудование |
|
Организация начала урока. Подготовка учащихся к работе на уроке |
2 минуты |
Приветствие, выявление отсутствующих; проверка готовности учащихся к уроку; готовность наглядных пособий. Раскрытие общей цели урока |
Кратковременность оргмомента; быстрое включение всех учащихся в деловой ритм; полная готовность класса и оборудования к уроку |
Фронтальная |
Доска, мел |
II. Актуализация ЗУН
|
Дидактическая задача этапа |
Время |
Содержание деятельности учителя |
Условия получения положительного результата |
Форма работы |
Оборудование |
|
Подготовка к активной УПД на основном этапе урока. Подготовка учащихся к тому виду учебно-познавательной деятельности, который будет доминировать на основном этапе урока. Актуализация опорных знаний и умений, формирование познавательных мотивов |
7-10 минут |
Постановка триединой дидактической цели урока; организация действий учащихся по ее принятию |
Умение определять и ставить триединые дидактические цели урока; владение приемами организации учащихся на деятельность по принятию цели |
Фронтальная, групповая |
Компьютер, проектор, доска, мел |
III. Деловая игра
|
Дидактическая задача этапа |
Время |
Содержание деятельности учителя |
Условия получения положительного результата |
Форма работы |
Оборудование |
|
Формирование у учащихся новых знаний, умений навыков. Сформировать у учащихся конкретные представления об изучаемых фактах, явлениях, процессах, их сущности, связи; выделить главное, провести обобщение вместе с учащимися; на основе знаний выработать умения |
7-10 минут |
Организация самостоятельной работы учащихся; восприятия учащимися нового материала, его осмысление, обобщение, осознание, систематизация, конкретизация |
Опора на жизненный опыт учащихся; индивидуальный подход по дозе помощи; организация учащихся на оперирование успеваемым содержанием |
Фронтальная, индивидуальная |
Доска, мел |
IV. Подведение итогов.
|
Дидактическая задача этапа |
Время |
Содержание деятельности учителя |
Условия получения положительного результата |
Форма работы |
Оборудование |
|
Подведение итогов урока. Анализ успешности овладения знаниями и способами деятельности; показать типичные недостатки в знаниях, умениях, навыках |
2 минуты |
Дать общую характеристику класса, показать успешность овладения содержанием урока; вскрыть недостатки, показать пути их преодоления |
Умение быстро схватывать типичное в успешности усвоения и недостатков, умение учесть реальные учебные возможности |
фронтальная |
|
Ход урока:
I. Организационный момент.
Здравствуйте, ребята! Дежурный, кто отсутствует на уроке? (записать отсутствующих)
II. Актуализация ЗУН
Вспомним основные виды графиков функций
(Слайд 2-5)
III. Закрепление материала
Сейчас используя все то, что мы только что вспомнили попробуем следующее задание (Слайд 6)
1. Найдите все значения a, при каждом из которых система уравнений
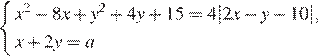
имеет более двух решений.
 Рассмотрим
первое уравнение системы. Мы видим, что данное уравнение распадается в
совокупность двух систем
Рассмотрим
первое уравнение системы. Мы видим, что данное уравнение распадается в
совокупность двух систем
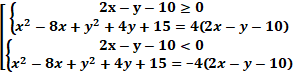
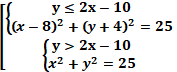
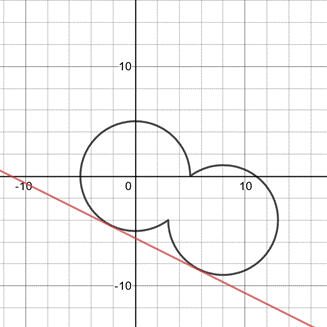
Рассмотрим графики в редакторе desmos
Найдем значения параметра a, при которых система имеет более 2 решений.
2 решения система имеет в случае касания окружностей(точки А и D) и выполняется условие: ![]() (Слайд 7-8)
(Слайд 7-8)
Получим уравнение: 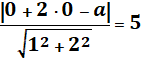
Откуда ![]()
3 решения система имеет в случае, когда прямая проходит через точку пересечения двух окружностей. Точки В и С (Слайд 9-10)
Найдем их координаты, решив систему
![]() , получим точки (3;-4) и (5;0).
, получим точки (3;-4) и (5;0).
Подставив эти координаты в уравнение прямой с параметром, получим: ![]()
Четыре решения система имеет между точками касания и полученными точками.
В остальных случаях либо нет решения, либо два решения.
Получим окончательный ответ![]()
Ответ: ![]()
2. Найдите все значения параметра ![]() при каждом из которых наименьшее значение функции
при каждом из которых наименьшее значение функции ![]() больше -4.(Слайд 11)
больше -4.(Слайд 11)
т.е. ![]() .
.
![]()
![]()
![]()
Введем две функции
![]() и
и![]()
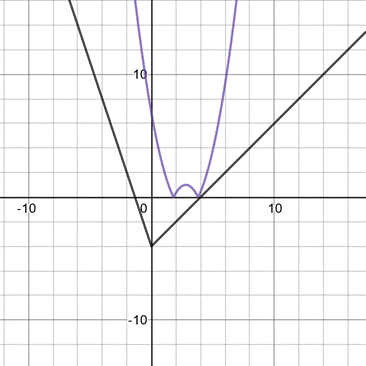
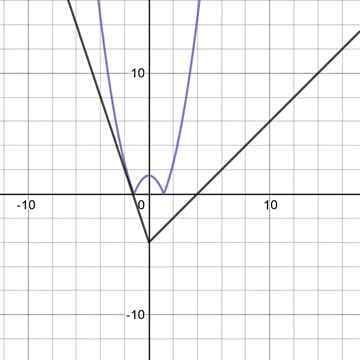
Рассмотрим первый случай, когда парабола касается прямой. Точка А (Слайд 12)
Запишем условия этого. В точке касания ветви параболы направлены вверх
и касается она прямой ![]() .
.
Получим уравнение ![]() , которое должно иметь 1 решение. Тогда
, которое должно иметь 1 решение. Тогда ![]()
Во втором случае парабола точно проходит через точку с координатамиВ(4;0). (Слайд 13)
Значит, ![]() 2 или
2 или ![]() . Проверив найденные значения, получим, что
. Проверив найденные значения, получим, что
![]()
Тогда получим![]()
IV. Домашнее задание
(Слайд14)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.