Решение задач модуль «Геометрия» демонстрационная версия ОГЭ по математике вариант №30

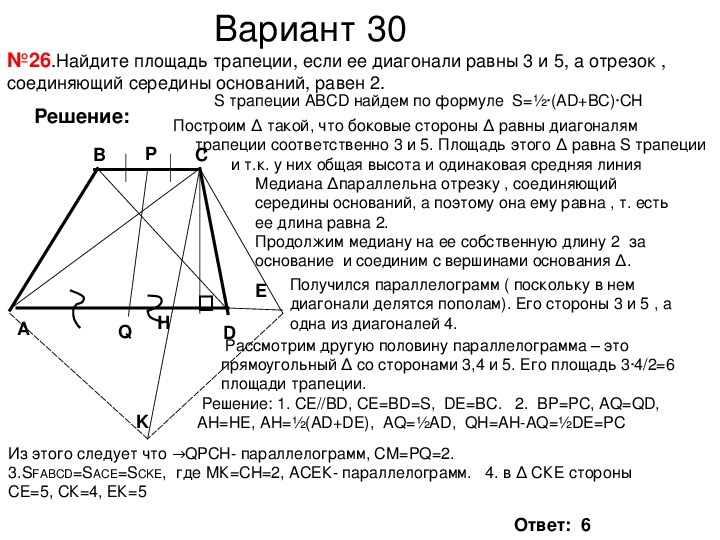
Вариант 30 №26.Найдите площадь трапеции, если ее диагонали равны 3 и 5, а отрезок ,  соединяющий середины оснований, равен 2. S трапеции АВСD найдем по формуле  S=½∙(AD+BC)∙СН Решение: В P А Н Q Построим ∆ такой, что боковые стороны ∆ равны диагоналям                трапеции соответственно 3 и 5. Площадь этого ∆ равна S трапеции              и т.к. у них общая высота и одинаковая средняя линия С Медиана ∆параллельна отрезку , соединяющий  середины оснований, а поэтому она ему равна , т. есть  ее длина равна 2. Продолжим медиану на ее собственную длину 2  за  основание  и соединим с вершинами основания ∆. Получился параллелограмм ( поскольку в нем  Е диагонали делятся пополам). Его стороны 3 и 5 , а  одна из диагоналей 4. D  Рассмотрим другую половину параллелограмма – это  прямоугольный ∆ со сторонами 3,4 и 5. Его площадь 3∙4/2=6  площади трапеции. K  Решение: 1. CE//BD, CE=BD=S,  DE=BC.   2.  BP=PC, AQ=QD,  AH=HE, AH=½(AD+DE),  AQ=½AD,  QH=AH­AQ=½DE=PC Из этого следует что  QPCH­  3.SFАВСD=SACE=SCKE,  где МК=СН=2, АСЕК­ параллелограмм.   4. в ∆ СКЕ стороны СЕ=5, СК=4, ЕК=5    параллелограмм, СМ=PQ=2.    → Ответ:  6