
Задачи ЕГЭ по теме «Пирамида»
B 13 № 901. В правильной
треугольной пирамиде ![]() медианы
основания
медианы
основания ![]() пересекаются
в точке
пересекаются
в точке ![]() . Площадь
треугольника
. Площадь
треугольника ![]() равна
2; объем пирамиды равен 6. Найдите длину отрезка
равна
2; объем пирамиды равен 6. Найдите длину отрезка ![]() .
.
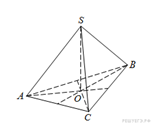
Пояснение.
Отрезок ![]() высота
треугольной пирамиды
высота
треугольной пирамиды ![]() , ее
объем выражается формулой
, ее
объем выражается формулой
![]()
Таким образом,
![]()
Ответ: 9.
B 13 № 911. В правильной
четырехугольной пирамиде ![]() точка
точка ![]() –
центр основания,
–
центр основания, ![]() –
вершина,
–
вершина, ![]() ,
, ![]() . Найдите
боковое ребро
. Найдите
боковое ребро ![]()
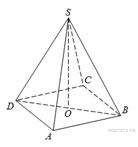
Пояснение.
В правильной пирамиде
вершина проецируется в центр основания, следовательно ![]() является
высотой пирамиды. тогда по теореме Пифагора
является
высотой пирамиды. тогда по теореме Пифагора
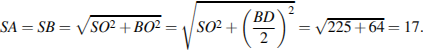
Ответ: 17.
B 13 № 920. В правильной
треугольной пирамиде ![]() точка
точка ![]() –
середина ребра
–
середина ребра ![]() ,
, ![]() –
вершина. Известно, что
–
вершина. Известно, что ![]() =3, а
площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка
=3, а
площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка ![]() .
.
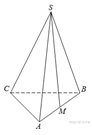
Пояснение.
Найдем площадь
грани ![]() :
:
![]()
Отрезок ![]() является
медианой правильного треугольника
является
медианой правильного треугольника ![]() , а
значит, его высотой. Тогда
, а
значит, его высотой. Тогда
![]()
Ответ: 10.
B 13 № 27074. Объем параллелепипеда ![]() равен
9. Найдите объем треугольной пирамиды
равен
9. Найдите объем треугольной пирамиды ![]() .
.
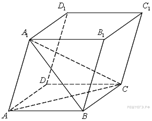
Пояснение.
Объем параллелепипеда
равен ![]() ,
где
,
где ![]() –
площадь основания,
–
площадь основания, ![]() –
высота. Объем пирамиды равен
–
высота. Объем пирамиды равен
![]() ,
,
где ![]() –
площадь основания пирамиды, по построению равная половине площади
основания параллелепипеда. Тогда объем пирамиды в 6 раз меньше объема
параллелепипеда.
–
площадь основания пирамиды, по построению равная половине площади
основания параллелепипеда. Тогда объем пирамиды в 6 раз меньше объема
параллелепипеда.
Ответ: 1,5.
B 13 № 27085. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
Пояснение.
Объёмы подобных тел относятся как куб коэффициента подобия. Поэтому если все ребра увеличить в 2 раза, объём увеличится в 8 раз.
Это же следует из формулы
для объёма правильного тетраэдра ![]() ,
где
,
где ![]() —
длина его ребра.
—
длина его ребра.
Ответ: 8.
B 13 № 27089. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
Пояснение.
Объем пирамиды равен
![]() ,
,
где ![]() –
площадь основания, а
–
площадь основания, а ![]() –
высота пирамиды. При увеличении высоты в 4 раза объем пирамиды
также увеличится в 4 раза.
–
высота пирамиды. При увеличении высоты в 4 раза объем пирамиды
также увеличится в 4 раза.
Ответ: 4.
B 13 № 27113. Объем треугольной
пирамиды ![]() , являющейся
частью правильной шестиугольной пирамиды
, являющейся
частью правильной шестиугольной пирамиды ![]() ,
равен 1. Найдите объем шестиугольной пирамиды.
,
равен 1. Найдите объем шестиугольной пирамиды.
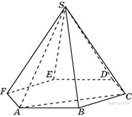
Пояснение.
Данные пирамиды
имеют общую высоту, поэтому их объемы соотносятся как площади их оснований.
Площадь правильного шестиугольника со стороной ![]() равна
равна ![]() Площадь
же равнобедренного треугольника
Площадь
же равнобедренного треугольника ![]() с
боковой стороной
с
боковой стороной ![]() и
углах при основании
и
углах при основании ![]() равна
равна ![]() Получаем,
что площадь шестиугольника больше площади треугольника
Получаем,
что площадь шестиугольника больше площади треугольника ![]() в
в
![]() раз
и равна 6.
раз
и равна 6.
Ответ: 6.
B 13 № 27114. Объем правильной
четырехугольной пирамиды ![]() равен
12. Точка
равен
12. Точка ![]() –
середина ребра
–
середина ребра ![]() . Найдите
объем треугольной пирамиды
. Найдите
объем треугольной пирамиды ![]() .
.
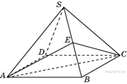
Пояснение.
Площадь основания
пирамиды ![]() по
условию в 2 раза меньше площади основания пирамиды
по
условию в 2 раза меньше площади основания пирамиды ![]() .
Также высота данной треугольной пирамиды в 2 раза меньше высоты пирамиды
.
Также высота данной треугольной пирамиды в 2 раза меньше высоты пирамиды ![]() (т.к.
точка
(т.к.
точка ![]() –
середина ребра
–
середина ребра ![]() ). Поскольку
объем пирамиды равен
). Поскольку
объем пирамиды равен ![]() , то
объем данной треугольной пирамиды в 4 раза меньше объема пирамиды
, то
объем данной треугольной пирамиды в 4 раза меньше объема пирамиды ![]() и
равен 3.
и
равен 3.
Ответ: 3.
B 13 № 27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
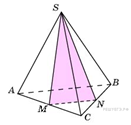
Пояснение.
Объем пирамиды ![]() . Площадь
основания отсеченной части меньше в 4 раза (так как высота и сторона
треугольника в основании меньше исходных в 2 раза), поэтому и объем
оставшейся части меньше в 4 раза. Тем самым, он равен 3.
. Площадь
основания отсеченной части меньше в 4 раза (так как высота и сторона
треугольника в основании меньше исходных в 2 раза), поэтому и объем
оставшейся части меньше в 4 раза. Тем самым, он равен 3.
Ответ: 3.
B 13 № 27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
Пояснение.
Площадь поверхности
тетраэдра равна сумме площадей его граней, которые равны ![]() . Поэтому
при увеличении ребер вдвое, площадь поверхности увеличится в 4 раза.
. Поэтому
при увеличении ребер вдвое, площадь поверхности увеличится в 4 раза.
Ответ: 4.
B 13 № 27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Пояснение.
При увеличении ребер в 3 раза площади треугольников, образующих грани октаэдра, увеличатся в 9 раз, поэтому суммарная площадь поверхности также увеличится в 9 раз.
Ответ: 9.
B 13 № 27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Пояснение.
Площади подобных тел относятся как квадрат коэффициента подобия. Поэтому, если все ребра увеличены в 2 раза, площадь поверхности увеличится в 4 раза.
B 13 № 27175. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
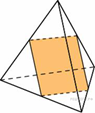
Пояснение.
В правильном тетраэдре
скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является
средней линией соответствующей грани, которая, как известно, в 2
раза меньше параллельной ей стороны и равна поэтому 0,5. Значит сечением
является квадрат со стороной 0,5. Тогда площадь сечения ![]() .
.
Ответ: 0,25.
B 13 № 27182. Объем параллелепипеда ![]() равен
12. Найдите объем треугольной пирамиды
равен
12. Найдите объем треугольной пирамиды ![]() .
.
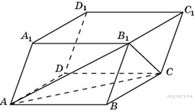
Пояснение.
Объем параллелепипеда
равен ![]() а
объем пирамиды равен
а
объем пирамиды равен ![]() . Высота
пирамиды равна высоте параллелепипеда, а ее основание вдвое меньше,
поэтому
. Высота
пирамиды равна высоте параллелепипеда, а ее основание вдвое меньше,
поэтому
![]()
Ответ: 2.
B 13 № 27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
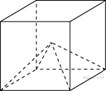
Пояснение.
Объем пирамиды равен
![]() .Ответ: 2.
.Ответ: 2.
Примечание.
Куб состоит из 6 таких пирамид, объем каждой из них равен 2.
B 13 № 77154. Найдите объем
параллелепипеда ![]() , если
объем треугольной пирамиды
, если
объем треугольной пирамиды ![]() равен
3.
равен
3.
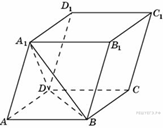
Пояснение.
Объем параллелепипеда
равен ![]() ,
где
,
где ![]() –
площадь основания,
–
площадь основания, ![]() –
высота. Объем пирамиды равен
–
высота. Объем пирамиды равен ![]() ,
где
,
где ![]() –
площадь основания пирамиды, равная половине площади основания
параллелепипеда. Тогда объем параллелепипеда в 6 раз больше объема
пирамиды
–
площадь основания пирамиды, равная половине площади основания
параллелепипеда. Тогда объем параллелепипеда в 6 раз больше объема
пирамиды ![]() .
.
Ответ: 18.
B 13 № 284351. В правильной
треугольной пирамиде ![]()
![]() —
середина ребра
—
середина ребра ![]() ,
, ![]() —
вершина. Известно, что
—
вершина. Известно, что![]() ,
а
,
а ![]() . Найдите
площадь боковой поверхности.
. Найдите
площадь боковой поверхности.
Пояснение.
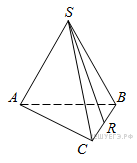 Площадь боковой поверхности правильной
треугольной пирамиды равна половине произведения периметра основания
на апофему:
Площадь боковой поверхности правильной
треугольной пирамиды равна половине произведения периметра основания
на апофему:
![]()
Ответ:3.
B 13 № 284356. В правильной
треугольной пирамиде ![]() медианы
основания пересекаются в точке
медианы
основания пересекаются в точке ![]() .
Объем пирамиды равен
.
Объем пирамиды равен ![]() ,
, ![]() . Найдите
площадь треугольника
. Найдите
площадь треугольника ![]() .
.
Пояснение.
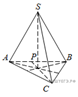 Основание пирамиды — равносторонний
треугольник, поэтому,
Основание пирамиды — равносторонний
треугольник, поэтому, ![]() является
центром основания, а
является
центром основания, а ![]() —
высотой пирамиды
—
высотой пирамиды ![]() . Ее
объем вычисляется по формуле
. Ее
объем вычисляется по формуле ![]() .
Тогда
.
Тогда
![]() .
.
Ответ: 3.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.