
САМОАНАЛИЗ
урока алгебры и начал анализа в 10б классе по теме «Тригонометрические уравнения»
Преподавание ведется по учебнику для учащихся общеобразовательных учреждений (базовый уровень), авторы А.Г.Мордкович и др. Издательства «Мнемозина». Москва 2011.
Этот урок проводится в классе, где большая часть учащихся имеют слабые знания, умения и навыки, у них отсутствует познавательный интерес и есть группа, состоящая из 3-х человек, которая сознательно и добросовестно готовится к занятиям.
Главный недостаток класса в том, что они шумные, с трудом настраиваются на работу и легко могут переключаться с полезного занятия на безделье, отвлечься, поэтому весь урок приходится поддерживать внимание, переключать с одного вида работы на другой.
Урок проводится в системе изучения раздела «Тригонометрические уравнения» по параграфу 18. Тип урока – урок закрепления – обусловлен тем, что это третий урок по данному параграфу. Урок органично связан с предыдущим: в ходе урока закрепляется материал, изученный на предшествующем занятии, закрепляется определение обратных тригонометрических функций, решение простейших тригонометрических уравнений, а также основные тригонометрические тождества.
Исходя из темы урока и его типа, обучающий аспект триединой цели урока можно сформулировать так: совершенствовать основные приемы преобразования и методы решения тригонометрических уравнений.
Образовательный аспект позволяет поставить такие развивающие цели: максимально выявить затруднения учащихся для установки верного варианта решения на основе самоконтроля, самоанализа. Считаю необходимым продолжить воспитание учащихся доброжелательности друг к другу, умение слушать, оказывать взаимопомощь.
1. Организационный момент, имеющий целью воспитание культуры поведения и учебного труда, настраивание учащихся на серьезную работу прошел быстро, т.к. это стало привычным делом для них перед каждым уроком.
2. Мобилизирующий этап способствовал для определения темы и целей урока. Ученики выполняли устные упражнения, восстанавливая знания, необходимые для решения более сложных тригонометрических уравнений.
3. Учащиеся смогли сами сформулировать тему и цели урока. Учащиеся выступали в роли учителя, что способствовало повышению познавательного интереса к уроку, сотворчеству между учителем и учениками.
4. Домашнее задание проверялось учителем, учащиеся сдали тетради на проверку.
5. Учащиеся составили алгоритм решения тригонометрического уравнения, записали его в тетрадь.
6. Задание «Найди ошибку» способствовало поиску решения тригонометрического уравнения, способствовало выявлению пробелов в знаниях учащихся.
7. Задания разноуровневые, с выбором ответа. Работа с разноуровневыми заданиями позволила осуществить обратную связь со всеми учениками. Это способствовало реализации принципа научности и доступности. При проверке заданий обе группы не оставались пассивными слушателями, они были нацелены на активное слушание ответов, выполняя посильные задания. Этот этап урока – этап совершенствования навыков решения тригонометрических уравнений.
8. Контроль за уровнем усвоения темы был проведен в форме разноуровневой самостоятельной работы, уровень сложности выбирался учениками. После сдачи работы на проверку учащимся сообщаются ответы к заданиям, которые заранее записанны на интерактивной доске. Затем подведён итог по выполнению заданий. Выяснено, кто получил ни одного верного ответа, получил один верный ответ и два верных ответа. Самопроверка работы показала, что нет ученика, который бы не справился вообще ни с одним заданием.
9. Домашнее задание дифференцированное, с правом выбора. Можно выполнить задания до черты, только после черты и все четыре задания. Такое домашнее задание является перспективой для урока – обобщения по разделу.
10. Подведение итогов урока – традиционный момент: учащиеся неплохо справляются с обобщением, оно необходимо, т.к. дисциплинирует, помогает повторить, закрепить на уровне обобщения.
Во время урока прослеживался логический переход от одного этапа урока к другому. После каждого этапа подведены итоги.
На уроке поддерживалась хорошая психологическая атмосфера за счёт добрых отношений, взаимопонимания учеников и учителя. Ответы учащиеся старались давать полные, поддерживалась любая инициатива ученика ответить.
Считаю, что поставленные задачи удалось реализовать на данном уроке.
Тема урока. Решение тригонометрических уравнений
Цели урока. Совершенствовать основные приёмы преобразования и методы решения тригонометрических уравнений; максимально выявить затруднения учащихся для установки верного варианта решения на основе самоконтроля, самоанализа, проверить уровень усвоения учебного материала.
Оборудование. Таблицы:
1.Формулы тригонометрии
2.Решение тригонометрических уравнений(простейших)
3.Интереактивная доска
Ход урока
I.Организационный момент.
II.Проверка домашнего задания. Учащиеся сдают тетради на проверку.
III.Актуализация знаний учащихся.
1. Повторение. Устная работа (задания с использованием интерактивной доски).
1. Вычислить
arccos![]()
arcsin-![]()
arcos(![]() )
)
arctg![]()
arcctg(-![]() )
)
Дать определение arcsin a, acrcos a, arctg a, arcctg a.
2. Какие значения может принимать выражение
arcsin![]()
arccos![]()
3. Найди область определения каждого из выражений
аrcsin2x
аrccos3x
аrcctg4x
аrcsin(х-2)
4. Решить уравнения
a) sinx=-1 г) 2cosx=0 ж) tgx=1
б) sin5x=1,02 д) cos2x=1 з) tgx=-![]()
в) sin![]() x=-
x=-![]() e) cosx=-
e) cosx=-![]() к)
к) ![]()
л) ![]() м)
м) ![]() н)
н) ![]()
о) ![]()
5. Составить алгоритм решения простейшего тригонометрического уравнения (на основе самоанализа выполнения устных упражнений учащиеся составляют алгоритм решения простейшего тригонометрического уравнения).
IV. Решить уравнение. «Найди ошибку».
Применён метод поиска решения тригонометрических уравнений с целью выявления пробелов в знаниях учащихся.
1. ![]() Верное
решение:
Верное
решение:
![]()
![]()
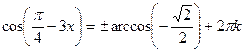
![]()
![]()
![]()
![]() ОШИБКА
ОШИБКА ![]()
![]()
![]()
![]()
![]()
![]()
2. ![]() Верное решение:
Верное решение:
![]()
![]()
![]()
![]()
![]()
![]()
![]() Пусть
Пусть ![]() ,
, ![]()
![]()
![]()
![]() ОШИБКА
ОШИБКА ![]()
![]() ОШИБКА
ОШИБКА ![]()
1) ![]() 1)
1)
![]() 2)
2) ![]()
![]() ,
, ![]() ОШИБКА
ОШИБКА ![]() ,
,![]()
![]()
2) ![]()
![]() ,
, ![]() ОШИБКА
ОШИБКА
Ответ: ![]()
![]()
После выполнения данного задания учащиеся исправляют у доски ошибки и приходят к единому ответу.
V. Задания разноуровневые по группам (задания на бумаге с разным цветом).
Решить уравнения (с выбором ответа). (уровень сложности В. Учащиеся тем самым готовятся к ЕГЭ по математике). За доской 4 ученика.
1 группа 2 группа
В1 ![]() B1
B1 ![]()
1) ![]() ,
,
![]()
![]() 1)
1)
![]()
![]()
![]()
2) ![]() ,
,
![]()
![]() 2)
2)
![]() ,
, ![]() ,
,
![]()
3) ![]() ,
,
![]() ,
, ![]() 3)
3)![]() ,
, ![]() ,
,![]()
В2 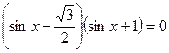 В2
В2
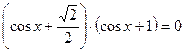
1) ![]() ,
, ![]() ,
, ![]() 1)
1)
![]() ,
,![]() ,
,![]()
2) ![]() ,
, ![]() ,
, ![]() 2)
2)
![]() ,
, ![]() ,
,
![]()
3) ![]() ,
, ![]() ,
, ![]() 3)
3)
![]() ,
,![]() ,
,
![]()
Код ответа:
1 группа: 22
2 группа: 21
После того, как выяснен код ответа, обнаруженная ошибка подробно рассматривается решением задания у доски.
VI. Этот этап урока организован так: учащимся даны задания по вариантам (за доской 2 ученика).
Выполнив своё задание, ученик приступает к решению задания другого варианта. Этот этап – этап совершенствования навыков решения тригонометрических уравнений.
1) ![]()
Решение:
![]()
![]()
а) ![]() или б)
или б) ![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]() ,
, ![]()
Ответ: ![]() ,
, ![]() ,
, ![]()
2) ![]()
Решение:
![]()
![]()
![]()
![]()
а) ![]() или б)
или б)
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]()
![]()
VII. Самостоятельная работа. На этом этапе урока осуществляется контроль знаний учащихся (после сдачи работ учащимся сообщаются ответы к заданиям).
Решить уравнения:
1 группа
1. ![]() Ответ:
Ответ: ![]()
2. ![]() Ответ:
Ответ: ![]()
![]()
2 группа
1. ![]() Ответ:
Ответ: ![]()
2. ![]()
Ответ: ![]() ,
, ![]()
Ответы к заданиям записаны на доске и сообщены учащимся после сдачи работы. Тем самым ученики были озадачены нахождением верного решения.
VIII. Домашнее задание разноуровневое. Каждый ученик получил задание по карточке.
Решите уравнение
1. ![]() и укажите
корни на отрезке
и укажите
корни на отрезке ![]()
Ответ: ![]() корни,
принадлежащие отрезку
корни,
принадлежащие отрезку ![]() .
.
2.
Решите уравнение ![]()
Ответ: ![]() ;
; ![]()
3.
Решите уравнение ![]()
Ответ: ![]() ;
; ![]()
Укажите корни, принадлежащие отрезку ![]()
Ответ: ![]() ;
;
![]()
4.
Решите уравнение ![]()
Укажите корни, принадлежащие отрезку ![]()
Ответ: ![]()
Отрезку принадлежат корни: ![]()
IX. Итог урока.
Что повторили на уроке? Что нового узнали на уроке (составлен алгоритм решения тригонометрического уравнения).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.