Статья "Технология уровневой дифференциации в личностно ориентированном обучении математике"

Технология уровневой дифференциации

в личностно ориентированном обучении математике.

Из всего накопленного опыта и имеющихся знаний хочу поделиться используемой мной тех­нологией дифференцированного обучения в личностно ориентированном подходе к обучению.

Напомним, что под дифференциацией понима­ют такую систему обучения, при которой каждый ученик, овладевая некоторым минимумом обще­образовательной подготовки, являющейся обще­значимой и обеспечивающей возможность адап­тации в постоянно изменяющихся жизненных условиях, получает право и гарантированную воз­можность уделять преимущественное внимание тем направлениям, которые в наибольшей степе­ни отвечают его склонностям.

В обучении математике дифференциация име­ет особое значение, что объясняется спецификой самого учебного предмета. Объективно матема­тика - одна из самых сложных школьных дис­циплин и вызывает трудности у многих учащих­ся. В то же время большое их число имеет явно выраженные способности к этому предмету. Раз­рыв в возможностях восприятия курса учащими­ся весьма велик. Ориентация же на личность уче­ника требует, чтобы дифференциация обучения математике учитывала потребности всех школь­ников.

Различают два вида дифференциации.

Уровневая дифференциация выражается в том, что, обучаясь в одном классе, по одной програм­ме и учебнику, дети могут усваивать материал на различных уровнях. Определяющим при этом яв­ляется уровень обязательной подготовки. Его достижение свидетельствует о выполнении уче­ником минимально необходимых требований к усвоению содержания. На его основе формиру­ются более высокие уровни овладения материа­лом.

Профильная дифференциация (или дифферен­циация по содержанию) предполагает обучение разных групп школьников по программам, отлу­чающимся глубиной изложения материала, объемом сведений и даже номенклатурой рассматриваемых вопросов¹ (¹ - разновидностью профильного обучения является углубленное изучение математики, обеспечивающее продвинутый уровень математической подготовки и позволяющее учащимся добиваться хороших результатов). Однако высокий уровень учеб­ных требований естественным образом ограни­чивает число учащихся, охваченных этой формой обучения.

Оба вида дифференциации сосуществуют и вза­имно дополняют друг друга на всех ступенях школьного математического образования, хотя и в разном удельном весе. В основной школе пре­обладает уровневая дифференциация, не теряю­щая своего значения и в старших классах. На старшей ступени школы приоритет отдается раз­нообразным формам профильного изучения пред­метов. Вместе с тем дифференциация по содер­жанию может проявляться уже в основной шко­ле» где она осуществляется через кружковые за­нятия и факультативы.

В своей работе к дифференцированному обу­чению я подхожу постепенно, начиная с V клас­са. Первые два года посвящаю наблюдениям, изу­чению психологии детей, диагностике результа­тов обучения, накапливаю материал для непосредственного включения учащихся в дифферен­цированную работу. С VII по IX класс работаю с двумя-тремя группами учащихся дифференциро­ванно. Наконец в X и XI классах, учитывая их небольшую наполняемость (10 человек), веду индивидуальную работу с учащимися, поступаю­щими в вузы, и работу с малочисленными груп­пами.

Уровневая дифференциация

В основе уровневого дифференцированного обу­чения лежит планирование результатов обучения: выделение уровня обязательной подготовки и формирование на этой основе повышенных уров­ней овладения материалом. Сообразуясь с ними и учитывая свои способности, интересы, потребности, ученик получает возможность выбирать объем и глубину усвоения учебного материала, варьировать свою учебную нагрузку. Достижение обязательных результатов обучения становится тем объективным критерием, на основе которого может видоизменяться ближайшая цель каждого ученика и перестраиваться содержание его рабо­ты: либо его усилия направляются на овладение материалом на более высоких уровнях, либо продолжается работа по формированию важнейших опорных знаний и умений.

Благодаря такому подходу дифференцирован­ная работа получает прочный фундамент, приоб­ретает реальный, осязаемый и для учителя и для ученика смысл. Заметно увеличиваются возмож­ности для работы с сильными учениками, по­скольку учитель уже не должен спрашивать дан­ный на уроке материал в полном объеме со всех школьников. Кроме того, отпадает необходимость постоянно разгружать программу и снижать об­щий уровень требований, оглядываясь на слабых школьников.

Перечислю ряд важных условий, выполнение которых необходимо для успешного и эффектив­ного осуществления уровневой дифференциации.

• Выделенные уровни усвоения материала и обязательные результаты обучения должны быть открыты для учащихся.

Успех дифференцированного обучения (как и учеб­ного процесса в целом) в значительной степени зави­сит от познавательной активности школьников, от того, насколько они заинтересованы в собственной ра­боте. Ясное знание конкретных целей при условии их посильности, возможность выполнить предъявляемые учителем требования активизируют познавательную де­ятельность учащихся, причем на разных уровнях.

Если цели известны и посильны ученику, а их до­стижение поощряется, то для подростка нет ничего естественнее, как стремиться к их выполнению. По­этому открытость уровней подготовки способствует формированию положительных мотивов учения, со­знательного отношения к учебе, повышению само­оценки учащегося.

• Наличие определенных «ножниц» между уровнем требований и уровнем обучения.

Не следует отождествлять уровень преподавания материала с обязательным уровнем его усвоения. Пер­вый должен быть в целом существенно выше, иначе и уровень обязательной подготовки не будет достигнут, а учащиеся, потенциально способные усвоить боль­ше, не будут двигаться дальше.

Каждый ученик должен в полном объеме услышать предлагаемый материал со всеми доказательствами обоснованиями, ознакомиться с образцами рассуждений, на каких-то этапах участвовать в решении более сложных задач. Иначе говоря, давая всем одинаковый объем материала, мы устанавливаем различные ни требований к его усвоению.

• В обучении должна быть обеспечена последовательность в продвижении ученика по ypовню.

Не следует предъявлять более высоких требований тем учащимся, кто не достиг уровня обязательной подготовки. Трудности в учебной работе должны быть для школьников посильными, соответствующими индивидуальному темпу овладения материалом на каждом этапе обучения. В то же время если для одних учащихся необходимо продлить этап отработки основных, опорных знаний и умений, то других не следует необоснованно задерживать на этом этапе.

• Добровольность в выборе уровня усвоения отчетности.

Каждый ученик имеет право добровольно и сознательно решать для себя, на каком уровне ему усваивать материал.

Такой подход позволяет формировать у школьника познавательную потребность, навыки самооценки, планирования и регулирования своей деятельности.

• Содержание контроля и оценка должны отражать принятый уровневый подход.

Контроль должен предусматривать проверку достижения всеми учащимися обязательных результат обучения, а также дополняться проверкой усвоенного  материала на более высоких уровнях.

Уровневая дифференциация может осуществляться в разной форме (ее выбор во многом зависит от методов и приемов работы учителя, особенностей класса, возраста учащихся и т.д.). В качестве одной из основных предлагается формирование мобильных групп, деление на которые происходит на основе критерия достижения уровня  обязательной подготовки.

Группы могут формироваться для работы и на обычных уроках, и на дополнительных занятиях. Отметим, что в процессе самостоятельной деятельности учащихся не стоит ограничиваться лишь дифференцированным подходом, следует варьиро­вать индивидуальную и фронтальную формы ра­боты в зависимости от этапа изучения темы, от потребности учащихся в помощи учителя.

Деление учащихся на группы в зависимости от достижения ими уровня обязательной подготов­ки носит объективный характер и при правильной организации не дает ученикам поводов для обид. Важно, что дети могут оценить собствен­ные силы и выбрать для себя уровень целей, со­ответствующий их потребностям и возможностям в данный момент, а со временем - перейти на более высокий уровень.

Профильная дифференциация

Математика входит в число обязательных учеб­ных предметов, при этом в общеобразовательной подготовке школьника она может иметь разный «удельный вес» как по времени, отводимому на ее изучение, так и по глубине и охвату рассматриваемого материала.

Математике принадлежит ведущая роль в фор­мировании алгоритмического мышления, умений не только действовать по известным алгоритмам, но и конструировать новые, т.е. тех умений, ко­торые необходимы для свободной ориентации в «компьютеризованном» мире. По данным неко­торых психологических исследований, логическое мышление ребенка формируется не ранее чем к 14-15 годам, поэтому неверно было бы прекра­тить «подпитку» интеллекта математикой у зна­чительной части учащихся на выходе из основ­ной школы. Правильное решение вопроса заклю­чается в резкой дифференциации обучения мате­матике в старшем звене, во введении курсов раз­ного объема и уровня сложности.

В зависимости от той роли, которую матема­тика может играть в образовании человека, выде­ляют два типа таких курсов.

Курс общекультурной ориентации (назовем его курсом А), который рассчитан на учащихся, рас­сматривающих математику только как элемент общего образования и не предполагающих ис­пользовать ее непосредственно в будущей профессиональной деятельности.

Курсы повышенного типа, обеспечивающие дальнейшее изучение математики и ее примене­ние в качестве элемента профессиональной подготовки. Выделим два основных курса повышен­ного типа.

Курс В предназначен для школьников, выбрав­ших для себя те области деятельности, где мате­матика играет роль аппарата, специфического средства для изучения закономерностей окружа­ющего мира.

Курс С ориентирован на учащихся, для кото­рых собственно математика является одной из ос­новных целей познания.

Таким образом, для старшей ступени школы целесообразно наличие трех основных математи­ческих курсов - А, В и С. Они призваны предо­ставить каждому ученику возможность изучать математику на уровне, соответствующем его интересам, способностям, склонностям. Этих кур­сов в целом достаточно для преподавания мате­матики по профилю любого направления.

Курс А могут выбрать учащиеся, которых инте­ресуют, например, языки, искусство, художест­венное творчество, спорт или предметно-практи­ческая деятельность. Он должен иметь выражен­ную гуманитарную направленность и быть ори­ентирован на знакомство с математикой как с областью человеческой деятельности; на умствен­ное развитие человека; на формирование знаний и умений, необходимых ему для свободной ори­ентации в современном мире. Обязательные тре­бования по усвоению курса А фактически долж­ны совпадать с базовым уровнем математической подготовки выпускников средней школы.

Курс В предназначен для учащихся с научным стилем мышления, выбравших для себя профи­ли естественно-научных и научно-гуманитарных направлений; химический, биологический, гео­графический, исторический, социологический, экономический и др. Курс В следует выстраи­вать с учетом того, что для изучающих его школь­ников математика является хотя и необходимым, но не самым важным предметом. Он должен обеспечивать овладение конкретными математи­ческими знаниями, позволяющими, в частнос­ти, выработать представления о применении математики в выбранной науке, и достаточны­ми для изучения математики в вузе соответству­ющего профиля.

Курс С - наиболее строгий и полный курс ма­тематики - ориентирован на учащихся, выбрав­ших для себя деятельность, непосредственно свя­занную с математикой, и как следствие - какой-то профиль из группы «математического направ­ления», например физико-математический или информационно- технологический.

Программу по каждому из курсов А, В и С це­лесообразно строить по «модульному принципу». В ней должно быть две части;

-       инвариантная, обязательная для изучения всеми, кто выбрал этот курс;

-       вариативная, состоящая из разделов, из ко­торых учитель может выбрать материал,  до­полняющий основную часть курса.

Необходимо сказать о возможности использования профильного обучения, начиная с VIII класса. К VIII классу некоторые школьники уже способны оценить привлекательные стороны ма­тематики, ее интеллектуальное и эстетическое воздействие. Развитие интереса к математике позволяет учащимся выбрать ее как предмет для последующего углубленного изучения. Разумеет­ся, этот выбор может оказаться ошибочным, не­адекватным истинным склонностям и способно­стям, поэтому организация углубленного изуче­ния математики должна быть максимально гиб­кой и обеспечивать возможность исправления ошибки.

Эти обстоятельства определяют роль VIII - IX классов в системе углубленного изучения матема­тики как ориентационного этапа, основной целью которого является диагностика, и обусловливают необходимость вариативности содержания обуче­ния. С одной стороны, оно должно предусматри­вать возможность изучения достаточно стройного и последовательного курса математики, а с другой - позволять практически избежать расширения общеобразовательного курса, достигая углубления только за счет повышения уровня сложности и раз­вивающей ценности решаемых задач.

О взаимосвязи дифференциаций

В дифференцированном обучении математике гуманна концепция единства уровневой и профиль­ной дифференциации, одна без другой неполноцен­на. Лишить ученика возможности в полной мере использовать тот или иной вид дифференциации - значит совершить антигуманный акт. По­лучать удовольствие от занятий математикой школьник сможет только тогда, когда дифферен­циация и индивидуализация (как предельная форма дифференциации) будут доступны ему в той степени, в какой он сам пожелает. В против­ном случае один ребенок будет учиться налегке, не напрягаясь, а другой - пытаться осилить не­посильное. Первый не найдет применения име­ющимся способностям и не реализует свой по­тенциал, второй будет чувствовать постоянное унижение, ощущать на каждом шагу собственную неполноценность и умственную убогость.

Изучение математики «на высоком» уровне нельзя осуществить в полной мере, если оно не опирается на профильную дифференциацию. Не использовать ее как рычаг для приведения в дей­ствие всех возможностей уровневой дифференциации - значит заранее понизить предполагае­мую эффективность обучения.

Профильная дифференциация направлена на углубленное изучение математики, расширение представлений о ее приложениях в различных об­ластях человеческой деятельности. Иначе гово­ря, мы имеем дело с качественно иным уровнем обучения математике. Поэтому профильная диф­ференциация является эффективным средством варьирования уровней обучения предмету, неза­висимо от того, в каком классе он преподается: в математическом, гуманитарном, техническом или общеобразовательном; без профильной диффе­ренциации невозможна эффективная уровневая дифференциация. Выбор профиля обучения ни­сколько не снижает значимости уровневой диф­ференциации, а изменяет лишь возможности ее осуществления.

Выделение двух видов дифференциации полез­но только для того, чтобы более разносторонне, глубоко, детально и полно изучить проблему диф­ференцированного обучения.

Подведем итоги.

Как некорректно рассуждать о времени, с ко­торого надо начинать гуманное обучение, так не­корректно говорить о времени начала дифферен­цированного обучения, являющегося неотъемлемой частью гуманизации. Обучение математике должно быть дифференцированным с детского сада.

- Ученику необходимо предоставить возмож­ность выбора той или иной дифференциации в любом возрасте, в любом классе, более того – на каждом уроке. Негуманно заявлять ученику, что он опоздал со своим выбором, что надо было сделать это раньше.

- При выборе форм дифференциации предпочтение нужно отдавать не экстенсивным, а ин­тенсивным формам.

- Дифференциацию следует осуществлять за счет различия в подходах и методах приобрете­ния знаний.

- Важно опираться на прогрессивные методы обучения, т.е. обучать школьников на наивысшем уровне их познавательных возможностей.

Формирование групп учащихся

В основу работы я закладываю изучение спо­собностей личности. В структуру математических способностей входят более десяти групп компо­нентов. Из них я выделяю две основные: быстро­ту усвоения и активность мышления.

Быстрота усвоения характеризуется следующи­ми категориями:

-       дословное повторение текста;

-       частичное повторение;

-       воспроизведение   50%  текста;

-       самостоятельное воспроизведение текста ранее изученного;

-       воспроизведение материала с помощью учителя;

-       воспроизведение с ошибками (но основная нить удерживается);

-       замедленное, невнятное воспроизведение текста;

-       умственная отсталость (затухание развития).
Активность мышления характеризуется такими категориями:

-       плодотворная работа на протяжении всего урока;

-       работа со «вспышками»;

-       неполная работоспособность;

-       быстрая утомляемость;

-       игнорирование заданий.

Материал для анализа перечисленных компо­нентов я беру прежде всего из наблюдений, по результатам которых заполняю следующую диа­гностическую таблицу.

 

Диагностику провожу в V классах, она включает в себя, в частности, разного рода анке­ты. Например, такую.

Анкета

1. Класс.

2. Фамилия, имя.

3. Где и кем работают родители?

4. Отношение родителей к математике. (Нужное подчеркнуть.)

Имеют математическое образование; применя­ют математику в своей работе; увлечены матема­тикой; не любят математику; не интересуются математикой.

5. Есть ли в домашней библиотеке математические книги (не учебники)?

6. Кто больше всего помогает тебе готовить уроки по математике?

7. Сколько времени занимает подготовка к уроку математики?

8. Почему ты учишь математику?

9. Хочешь ли ты знать больше, чем дается на уроке?

10.   Как дается тебе математика? (Нужное подчерк­нуть.)

Легко; много надо заучивать; трудно.

11.  Твое отношение к математике? (Нужное под­черкнуть.)

Люблю; учу, чтобы получить хорошую оценку, чтобы не ругали дома; скучно на уроках; не хочу ее учить.

12. Какими знаниями по математике ты владел до прихода в школу? (Нужное подчеркнуть.)

Счет до 10 и обратно; сложение в пределах десятка; решение простых задач.

13. Какого вида задания по математике тебе нра­вятся больше? (Нужное подчеркнуть.)

Задачи; примеры; задачи и примеры.

14. Мечтаешь ли ты связать свою жизнь с матема­тикой? (Нужное подчеркнуть.)

Хочу стать математиком; хочу поступить в вуз, куда надо сдавать математику; хочу знать как можно больше о разном.

Итак, в классе сформировались три группы уча­щихся, по-разному относящиеся к математике. Сообщаю ученикам, кто в какой группе оказал­ся; можно сделать это в шуточной форме: Считалкины, Решалкины и Смекалкины (группы отве­чают уровням А, В и С, см. таблицу). Ребята знают, что состав групп не закреплен раз и на­всегда. Со временем можно перейти из одной группы в другую в соответствии с результатами обучения и собственным желанием.

Методика дифференцированной работы на уроке

Итак, к VII классу передо мной три группы. Можно начинать поэтапное дифференцирование.

I этап. Дифференцированная домашняя работа

Считалкиным предлагаю задания, соответству­ющие обязательным результатам обучения.

Решалкиным даю такое же задание, к которому добавляю более сложную задачу.

Смекалкиным задание из учебника дополняю за­дачами из различных пособий.

II этап. Учет знаний учащихся на уроке

На этом этапе в классе выделяются консуль­танты - ребята из группы Смекаякиных. Сначала повторяю их работу, затем они помогают мне проверять работу остальных групп.

III этап. Организация базового повторения.

Ликвидирую выявленные проблемы в знаниях теоретического материала, разъясняю недочеты и ошибки, допущенные учениками в самостоятельных и контрольных работах. Планируемый для повторения материал записываю на доске. Создаю опорные конспекты с учащимися по темам.

Задания каждой группе предлагаю разные.

Считалкиным – «Выберите из данных ответов верный». «Исправьте ошибку в…».

Решалкиным – «назовите правило, по которому выполняли действие…», «Закончите решение…»

Смекалкиным – «Поясните причину допущенной ошибки», «Сформируйте определение понятий, использующихся в данной задаче»

IV этап. Проверка усвоения пройденного материала

Она включает самоконтроль, работу консультантов, выполнение самостоятельной роботе с последующей проверкой.

V этап. Изучение нового материала.

Дифференциация проявляется по отношению ко всем учащимся уже со второго урока по новой теме.

Смекалкины переходят от обязательных заданий к творческим.

Решалкины сосредотачиваются на упражнениях, требующих хорошего понимания основных положений темы.

Считалкины снова и снова возвращаются к основным моментам.

VI этап. Контроль знаний (проведение самостоятельных

и контрольных работ).

Считалкины выполняют задания по образцу.

Решалкины выделяют главное в решении.

Смекалкины работают с дополнительным материалом.

Подбор заданий.

Приведу пример дифференцированной самостоятельной работы по алгебре, в которой учащимся трех групп предлагаются различные задания.

Тема: Преобразование логарифмических выражений

Вычислить:

Считалкиным:

№1. 2  + 3

1) 22        2) 18        3) 12         4) другой ответ

№2. 2  + 3

1) 25        2) 5        3) -5         4) другой ответ

№3.   +

1) 0        2) 4+        3) 1        4) другой ответ

№4.   +

1) 1        2)         3) 0        4) другой ответ

№5.   – 3

1) 5         2) 9                3) 7        4) другой ответ

№6.   

1) -1        2) 0         3) 1        4) другой ответ

№7. 

1) 2        2) 0          3) -1        4) другой ответ

№8. 

1) 2        2) 0,3        3) 3        4) другой ответ

№9.   +

1) 3        2) -3        3) 8        4) другой ответ

№10. 

1) 6        2) 5         3) 10        4) другой ответ

№11. 

1) 49        2)        3) 14        4) другой ответ

№12. 

1) 9        2)3          3)         4) другой ответ

№13. 

1) 9        2)3         3)         4) другой ответ

№14. 

1)         2)        3) другой ответ

№15. 

1)    минус        2) плюс       3) другой ответ

 

Решалкиным

1.    

2.    

3.    

4.    

5.    

6.     +

7.     +

8.    

9.    

10.

11.

12.

13.

14.       

15.       

16.       

 

Смекалкиным.        Вычислить.

1.    

2.    

3.     +

4.     ·

5.                  

6.                  

7.                  

8.                  

9.                  

10.              

11.              

12.              

13.               Определить знак числа

 

А вот примеры двух дифференцированных работ, задания которых сопровождаются указаниями по их выполнению (при этом у всех групп примеры или задачи одни и те же).

Тема : Решение логарифмических уравнений.

Считалкиным.

Заполните пропущенные места в решении.

№1.

Решение.

 

 

 

 

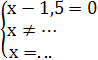
Проверка. Если х=…, то

Ответ: …

 

Решалкиным.

Решите уравнение.

Указания.

1)  Заменимте разность логарифмов, логарифмом частного.

2)  Приведите уравнение к дробно-рациональному.

3)  Учтите условие равенства дроби нулю.

4)  Решите уравнение.

5)  Сделайте проверку корней уравнения.

6)  Запишите ответ.

Смекалкиным.

Решите уравнение

 

Тема: Решение логарифмических неравенств.

Считалкиным.

1)  Решить неравенство  

2)  Заполните пропущенные места в решении.

 

Решение.

 

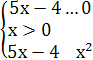
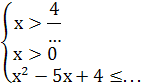
1) 

знаки

 

-1

2) 

 

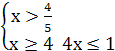
3) хϵ…

Ответ:

 

Решалкиным.

Указания.

1)    Установить ОДЗ.

2)    Уберите множитель 2, применив свойство логарифм степени.

3)    Учтите, что функция  является убывающей (t>0)

4)    Сравните полученные выражения.

5)    Решите систему неравенств.

6)    Запишите ответ.

 

Смекалкиным.

Решите неравенство

Ответ: х≥…