Поделиться
задачи геом егэ.docx
Вариант 1
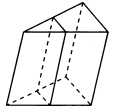
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Вариант 2
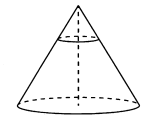
6. Площадь основания конуса равна 72. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 6 и 12, считая от вершины.
Вариант 3
1. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
2. Найдите
площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр,
радиус основания которого равен 2
, а высота равна 2.
3.
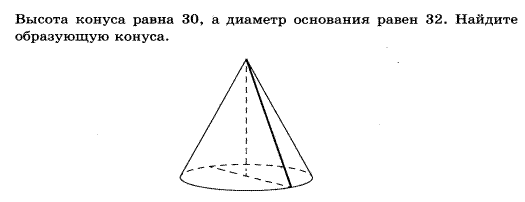
Вариант 4
2.Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
3.Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 11. Найдите площадь поверхности шара.
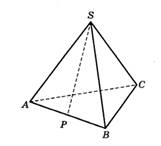
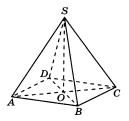
4.В правильной четырехугольной пирамиде SABCD точка O — центр
основания, SO = 28, BD = 42. Найдите боковое ребро SC.
6. Найдите боковое ребро правильной четырехугольной призмы, если сторона
ее основания равна 9, а площадь поверхности равна 522.
Ответы
|
Вариант задание |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
39 |
4,8 |
3,5 |
72 |
20 |
288 |
|
2 |
7 |
158 |
15 |
117 |
4 |
8 |
|
3 |
2 |
36 |
2,5 |
34 |
48 |
110 |
|
4 |
160 |
340 |
166,5 |
35 |
4 |
10 |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
