Сборник логических задач для учащихся 5 классов

Задачи логического характера, предложенные 5-классникам

Предисловие
Публикация содержит сборник 51 задач преимущественно логического характера с полным и кратким решением. Этот сборник предлагали как задание на лето учащимся, зачисленным в 5 (математический) класс Киево-Печерского лицея № 171 «Лидер» в июне 2013 года. Автор столкнулся с этим сборником как отец ученицы, которая решала эти задачи. Собственно, с решением большинства задач проблем не было. Но были проблемы со кратким описанием решения.

Введение пропедевтического курса логики в начальной школе, например, со второго класса, никак не решает и не облегчает решение проблемы речи, символьной записи и наглядности. Обычно в рабочих тетрадях отведенного на решение места достаточно для написания ответа и намеков на решение. Это становится особенно очевидным, если учесть размер букв почерка школьника начальной школы. Иначе говоря, авторы пособий не считают нужным обучать учащихся начальной школы так, чтобы не было необходимости их переучивать. Проблему невозможно решить, введя отдельные тетради для записи полноценного решения. Скорость писания учащихся начальной школы такова, что записи будут длиться существенно дольше времени, в течение которого учащийся способен концентрировать внимание. Чтобы не отразить желание детей заниматься такими задачами и математикой вообще, учителя обычно не обращают внимание на совершенство решения таких задач в начальной школе.

Если еще можно и нужно надеяться от учащихся самостоятельно породить идеи решения, то самостоятельно овладеть общепринятыми приемами выражения мнения для них будет не под силу. Даже в старших классах. Когда-то нужно начинать знакомить учащихся с приемами краткой записи и требовать от них аналогичного оформления. Как уже сказано, в 5 класс — рано. После 8 класса поздно, потому что этому помешает мощный поток понятийного аппарата многих предметов. В том числе и математики. По мнению автора публикации, начинать лучше всего в 6 классе, а результаты такой изнурительной (и для ученика, и для учителя) работы проявятся не раньше, чем за три года.

Подготовка в педагогических вузах и в прошлом, и сейчас не предполагает выработку устойчивых навыков решения и обучения решению логических задач. Поэтому помогать нужно и учащимся, и студентам, и учителям. Хотя бы представлением таких решений, что все понятно и ни слова выбросить невозможно . Особое внимание следует уделять тем задачам, которые при первом знакомстве непосильны для учащихся чисто по психологическим соображениям. В данном сборнике это:

·                     № 2 — ответ зависит от толкования условия, не однозначного;

·                     № 16 - многовариантность ответа и сознательное избегание наглядности с целью краткого изложения;

·                     № 17 – многовариантность ответа и внимательное отношение к условию (в котором не сказано, что на родительское собрание пришли родители всех учащихся;

·                     № 29 - требуется доказать ложное утверждение, поэтому нужно представить контрипримеры;

·                     № 44 — множество решений бесчисленно и существуют значения параметров задачи, при которых существенно меняется поведение исследуемой системы, что не очевидно из условия задачи.

Готовить нужно и к таким задачам. Ученик должен быть готов к каким-либо неожиданностям на контрольных, ВНО или олимпиадах (запланированных или пропущенных составителем задачи), а результат его работы не должен зависеть от наличия таких неожиданностей.
Публикация адресована учителям математики общеобразовательных учебных заведений и студентам математических специальностей педагогических университетов.

Цель публикации: познакомить с примерами максимально краткого оформления решения задач логического характера невысокой сложности.

Задание 1 . Можно ли квадрат 5×5 клеток разрезать на две одинаковые части таким образом, чтобы линия разреза шла сторонами клеток? Ответ обоснуйте.

Решение . При таком разрезании каждая клетка полностью попадает только в одну из фигур. В каждой из фигур будет натуральное количество клеток. Если фигуры одинаковы, то количество клеток у них одинаковое. В этом случае общее количество клеток квадрата должно быть парным. Но 25 – нечетное число, поэтому разрезать описанным способом квадрат на две разные фигуры невозможно.

Ответ: невозможно.

Задание 2 . Разделите квадрат 4×4 на четыре одинаковые части таким образом, чтобы линии разреза шли сторонами клеток. Сколько разных способов разрезания Вы найдете?

Ответ:



 

 

 

   

   

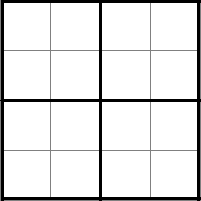
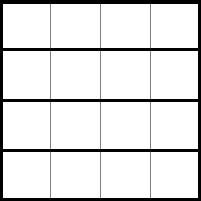
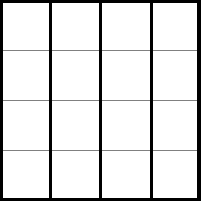
Количество способов разрезания: 6 с точностью до движений фигуры, 15, если стороны неподвижны.

Задание 3 . На столе лежат 5 красных и 5 синих палочек разной длины. Суммы длин палочек одного цвета одинаковы. Возможно ли распилить эти палочки таким образом, чтобы их потом можно было разместить парами палочек одинаковой длины и разного цвета?

Решение . Выложим палочки одного цвета вдоль прямой линии. Выложим палочки другого цвета вдоль параллельной линии таким образом, чтобы начатки и концы последовательностей палочек соприкасались. Двигая пилу от начала последовательности полочек до их конца, встретив стык палочек одного цвета, разрезаем палочку другого цвета. Получим нужное расположение парами. Так что разрезать можно.

Ответ: возможно.

Задание 4 . В комнате стоят табуретки и стулья. У каждой табуретки – 3 ножки, у каждого стула – 4 ножки. Если на всех стульях и табуретках посиживают люди, в комнате 39 ног. Сколько в комнате табуреток и сколько стульев?

Решение . Если на табуретке сидит человек, то есть всего 5 ног, а если на стуле, то 6. Составим таблицу, в которой через x обозначим количество стульев.

Ответ: 4 стула и 3 табурета.

Задание 5 . Три приятеля Петр, Анатолий и Виталий подошли к стоянке автомашин и мотоциклов. Любуясь машинами, Петр от скуки подсчитал все транспортные средства. Их оказалось 45. Анатолий подсчитал колеса – их оказалось 115. Виталий заметил, что мотоциклов с коляской было вдвое меньше, чем мотоциклов без коляски. Сколько машин было на стоянке?

Решение . Обозначим через х количество мотоциклов с коляской. Тогда:
3x – количество колес на мотоциклах с коляской;
2 x – количество мотоциклов без коляски;
4 x – количество колес на мотоциклах без коляски;
7 x– количество колес на всех мотоциклах.
Для разных величин x вычислим (115 – 7 x ) — количество колес, которые остаются для машин. Это количество должно быть кратно 4.

При x  > 16 есть: 115 –  x  > 0. Возможные величины x таковы: 1, 5, 9, 13. Проверим, при каком из них количество всех транспортных средств равно 45.

Ответ: 6 автомашин.

Задание 6 . Став в круг, разговаривают 4 девочки: Ася, Валя, Галя и Нина. Девочка в зеленом платье (не Ася и не Валя) стоит между девочкой в ​​фиолетовом платье и Ниной. Девочка в белом платье стоит между девочкой в ​​розовом платье и Валей. Какого цвета платье одела каждая девочка?

Решение . Составим прямоугольную таблицу, в которой первыми буквами имен назовем строки, а первыми буквами цветов назовем столбцы. В этой таблице обозначим плюсами или минусами без индексов непосредственные последствия простых предложений условия («+», если у девушки платье определенного цвета, иначе «–»). Заполним эту таблицу исходя из того, что в каждой строке и в каждом столбце должен быть один и только один плюс. Индексом справа снизу укажем номер логического шага.

Изобразим схему расположения (с точностью до точки зрения: сверху или снизу).

Если у Нины будет белое платье, то она должна стоять между девушкой в ​​розовом платье и Валей. Но рядом с ней Галя в зеленом платье. Эти условия не совместимы. Итак, Надя имеет розовое платье, а Ася – белое. Схема расположения приобретает такой вид,

что полностью согласовано с условием.

Ответ: Аcя - в белом платье, Нина - в розовом платье, Галя - в зеленом платье, Валя - в фиолетовом платье.

Задание 7 . В школе работают 18 учителей. Каждый из них либо добр, либо зол. Известно, что среди любых трех учителей хотя бы один хороший. Каково наиболее возможное число злых учителей?

Решение .

1.                 Если злых учителей нет, то среди любых трех учителей все хорошие – условие сбывается.

2.                 Если злой учитель один, то среди любых трех учителей 0 или 1 злой учитель — условие сбывается.

3.                 Если злых учителей 2, то среди любых трех учителей 0, 1 или 2 злых учителя – условие сбывается.

4.                 Если злых учителей 3 или больше, то среди любых трех учителей 0, 1, 2, 3 или более – условие не реализуется.

Ответ: 2.

Задание 8 . Дед вдвое сильнее Бабу, Баба втрое сильнее Внучки, Внучка в 4 раза сильнее Жучки, Жучка в 5 раз сильнее Кошки, Кошка в 6 раз сильнее Мишки. Без Мишки все остальное Репко вытащить не могут, а с ней – могут. Сколько нужно Мышек, чтобы они сами вытащили Репку?

Решение .
6 · 5 · 4 · 3 · 2 + 6 · 5 · 4 · 3 + 6 · 5 · 4 + 6 · 5 + 6 + 1 =
6 · 5 · 4 · 3 · (2 ​​+ 1) + 6 · 5 · 4 + 6 · 5 + 6 + 1 =
6 · 5 · 4 · (9 + 1) + 6 · 5 + 6 + 1 =
6 · 5 · 41 + 6 + 1 = 30 · 41 + 7 = 1230 + 7 = 1237.

Ответ: 1237 Мишок.

Задание 9. Длина лестницы между соседними этажами равна 10 м. Сколько метров нужно пройти, чтобы подняться с первого этажа на седьмой?

Решение . Нужно преодолеть (7 – 1) = 6 расстояний между этажами, что составляет 6·10 м = 60 м.

Ответ: 60 метров.

Задание 10 . В записи ***5 : 11 = ** замените звездочки цифрами таким образом, чтобы получить сверяемое равенство.

Решение . Условие задачи можно записать так ***5 = ** ⋅ 11. Запись в «столбик» выглядит так:

    **

× 11

  ----

    **

+**

  ----

  ***5

Анализируя разряд единиц имеем: запись двузначного числа — сомножителя 11 — заканчивается цифрой 5. При добавлении двух чисел в «столбик» в следующий разряд переносят не более 1. Для того чтобы произведение было четырехзначным числом необходимо, чтобы запись двузначного числа — сомножителя 11 — начинался цифрой 9. Есть:

    95

× 11

  ----

    95

+ 95

  ----

  1045

Ответ: 1045 : 11 = 95.

Задание 11 . Василий задумал целое число. Николай умножил его или на 5, или на 6. Евгений добавил к результату Николая или 5, или 6. Саша отнял от результата Евгения или 5, или 6. В результате получилось 73. Какое число задумал Василий?

Решение . В результате выполнения двух последних действий число возрастает на одно из следующих чисел:

+5 – 5 = 0;
+ 5 – 6 = –1;
+ 6 – 6 = 0;
+ 6 – 5 = 1

После выполнения первого действия получили одно из следующих чисел: 72, 73 или 74 при условии, что оно кратно 6 или 5. Следовательно, это число 72. А задуманное число в 6 раз меньше – 72 : 6 = 12

Ответ: 12. Задание

12. Для окрашивания поверхности куба требуется 6 г краски. После высыхания краски куб распилили на 8 одинаковых кубиков. Сколько нужны краски, чтобы раскрасить не закрашенные части их поверхности?

Решение . В кубе 6 одинаковых граней. На каждую грань потратили 6:6 = 1 (грамм краски). Если куб разделить на 8 одинаковых кубиков, каждое ребро нужно разделить пополам. Всего нужно произвести 3 разрезания. В каждом сечении – квадрат, одинаковый по размерам с гранью. Но для каждого разреза вновь кубики нужно красить с обеих сторон от разреза. Следовательно, покрасить нужно поверхность, площадь которой такая же, как у 6 граней. На это нужно потратить 6 г краски.

Ответ: 6 граммов.

Задание 13. У Андрея и Бориса вместе 11 орехов, у Андрея и Владимира – 12 орехов, у Бориса и Владимира – 13 орехов. Сколько всего орехов у Андрея, Бориса и Владимира вместе?

Решение . Обозначим первыми буквами имен ребят количество орехов в них. Имеем:

А+Б =11;
А+В =12;
Б + В = 13.

Каждая буква записана в двух уравнениях. Добавив правые и левые части всех трех уравнений, получим: 2 А  + 2 Б  + 2 В  = 36.

Разделив обе части последнего уравнения на 2, получим: А + Б + В  = 18.

Ответ: 18 орехов.

Задание 14. Вдоль беговой дорожки расставлены 19 флажков на одинаковом расстоянии друг от друга. Михаил стартует от первого флажка и бежит с постоянной скоростью. Через 7 секунд он оказывается около 7-го флажка. За какое время Михаил добежит до 19-го флажка?

Решение . От первого до 19 флажка расположено (19 – 1) = 18 промежутков. От 1-го по 7-е расположено (7 – 1) = 6 промежутков. Михаил все расстояние преодолеет за время, которое в 18:6 = 3 раза превышает 7 секунд, то есть за 21 секунду.

Ответ: Михаил добежит от первого до 19-го флажка за 21 секунду.

Задание 15. На доске записано 3 двухцифровых числа, запись одного из которых начинается на 5, другого — на 6, а третьего — на 7. Учитель попросил троих учеников выбрать произвольные два из этих трех чисел и прибавил их. Первый ученик получил 147, результаты второго и третьего – разные 3-цифровые числа, запись которых начинается с 12. Какие числа записаны на доске?

Решение . Заметим: 5+6=11, 5+7=12, 7+6=13. При добавлении двух чисел в следующий разряд переносят не более 1 единицы. Пусть записанные числа выглядят: 5 А , 6 В , 7 С (в этом решении такие записи будем истолковываться как записи двухцифровых чисел, а не как запись произведений). Есть:

·                     6 В + 7 С = 147,
60 + В + 70 + С = 147,
В + С = 147 – 130 = 17 = 9 + 8,
{ В, С } = {8, 9};

·                     5 А + 6 В = 12 Х = 120 + Х ,
110 + А + В = 120 + Х ,
А + В = 120 + Х – 110 = 10 + Х ≥ 10,
А ≥ 10 – В ;

·                     5 А + 7 С = 12 Y ,
50 + 70 + А + С = 120 + Y ,
120 + А + С = 120 + Y ,
А + С = 120 + Y – 120 = Y < 10,
А < 10 – С .

Есть: 10 – В ≤ А < 10 – С при В = 8 и С = 9 или В = 9 и С = 8.

2 = 10 – 8 ≤ А < 10 – 9 = 1 – такое невозможно.
1 = 10 – 9 ≤ А < 10 – 8 = 2 – такое сбывается при А = 1.

Ответ: 51, 69, 78.

Задание 16 . Расстояние между двумя авто на шоссе равно 100 км. Скорости машин составляют 80 км/ч и 60 км/ч. Каково будет расстояние между ними (вдоль шоссе) через час?

Решение. Введем на шоссе систему координат таким образом, чтобы в начальный момент одна из машин имела координату 0 и скорость v ₀ , другая – координату 100 (км) и скорость v ₁ , где:

·                     или v ₀ = ±60 км/ч и v ₁ = ±80 км/ч;

·                     или v ₀ = ±80 км/ч и v ₁ = ±60 км/ч.

Независимый выбор обоих знаков в обоих случаях никак не ограничен условием. Через промежуток времени t (в часах) координаты машин будут следующие (в километрах):

x ₀ = v ₀ t ;
x ₁ = v ₁ t + 100,

а расстояние между машинами составит:

| x ₁ – x ₀ | = | v ₁ t + 100 – v ₀ t | = | ( v ₁ – v ₀ ) t + 100 |

Подставив в последнюю формулу времяt = 1 и все допустимые варианты сочетания v ₀ и v ₁ , получим:
| (80+60) · 1+100 | = 240;
| (80 – 60) · 1+100 | = 120;
| (– 80 + 60) · 1 + 100 | =80;
| (– 80 – 60) · 1 + 100 | =40;
| (60+80) · 1+100 | = 240;
| (60 – 80) · 1+100 | =80;
| (– 60 + 80) · 1 + 100 | = 120;
| (– 60 – 80) · 1 + 100 | = 40.

Ответ: возможны следующие варианты: 40 км, 80 км, 120 км или 240 км.

Задание 17 . В классе 30 учащихся класса. Их родители пришли на собрание. Мам было 24, пап - 18. У скольких учеников на собрание пришли одновременно и папа, и мама?

Решение . Обозначим через:
М— количество учащихся, на которых пришла мама;
Т — количество учащихся, на которых пришел папа;
МТ — количество учащихся, на которых пришли мама и папа одновременно;
Y — количество учащихся, на которых пришел хотя бы один из родителей, В ≤ 30.

Есть:
( М – МТ ) — количество учащихся, на которых пришла только мама;
( Т – МТ ) — количество учащихся, на которых пришел только папа;
Y = ( М – МТ ) + МТ + ( Т – МТ ) = М + Т – МТ ,
откуда МТ = М + Т – Y ≥ 24 + 18 – 30 = 12.

С другой стороны:
МТ ≤ М= 24;
МТ ≤ Т = 18.

Окончательно имеем: 12 ≤ МТ ≤ 18.

Ответ: одно из следующих чисел: 12, 13, 14, 15, 16, 17, 18.

Задание 18 . В рюкзаке лежит 4 банки: две со сливками и две с молоком. Наугад вынимают 2 банка. Если они с одинаковым содержанием, то их используют на завтрак, а в рюкзак кладут банку с молоком. Если банки с разным содержанием, то их также используют на завтрак, а в рюкзак кладут банку со сливками. В конце концов в рюкзаке осталась одна банка. Что в ней: молоко или сливки?

Решение . Изобразим на схеме все возможные варианты манипуляций: В – банка со сливками, М – с молоком.

   2В+2М

    ↙ ↘

  3M 2В+1M

   ↓ ↙ ↓

  2M 2В

   ↓ ↙ 

  1M

Ответ: банка с молоком.

Задание 19 . Какое число должно стоять вместо знака * в последовательности: 7, 17, 37, 77, *, …, 317, …?

Решение . Для данной последовательности последняя цифра равна 7, а результат ее отбрасывания со степенью двойки, уменьшенной на 1. Также можно сказать, что результат отбрасывания 7 для следующего члена является удвоенным результатом отбрасывания для текущего члена, увеличенным на 1: 0, 1, 3, 7 , 15, 31, 63…

Ответ: 157.

Задание 20 . В магазин привезли 223 л масла в бидонах по 10 и 17 л. Сколько было бидонов?

Решение . Обозначим через А количество бидонов по 10 л, через В – количество бидонов по 17 л. Имеем:
223=10А + 17 В ⇔ 10 А = 223 – 17 В.

Переберем все возможные величины.

Есть: А = 7, B = 9, A + B = 16.

Ответ: 16 бидонов.

Задание 21 . На лесной лужайке собрались друзья: Попугай, Удав, Слоненок, Теля, Котенок, Обезьянка и Верблюженя. Попугай начал всех измерять. Оказалось, что Слоненок длиннее Теляты на 3 попугая, Верблюжонок длиннее Обезьянки также на 3 попугая, Теля длиннее Попугая на 7 попугаев, Верблюжонок длиннее Котенка на 6 попугаев, а суммарная длина всех равна длине Удава, длина которого длина8. Найдите длины друзей в попугаях.

Решение . Обозначим первые буквы имен персонажей их длины. Есть:
(1)   С = Т + 3 П ;
(2)   В = М + 3П ;
(3)   Т = 8 П ;
(4)   В = К + 6 П ;
(5)   У = 38 П ;
(6)   У = П+С+Т+К+М+В .

Выразим переменные через П :
(7)   С = 11 П – см.(1,3)
(8)   М = К + 3 П – см. (2,4)
(9)   М + К + В = В – П – С – Т = 18П – см. (6, 5, 7, 3)
(10)   В = М + 3 П = К + 6 П – см. (2, 8)
(11)   К + М + В = 3 К + 9 П – см.(10, 8)
(12)   К = (18 П – 9 П ): 3 = 3 П – см. (11, 9)
(13)   М = К + 3 П = 6 П – см. (12, 8)
(14)   В = К + 5 П = 9 П – см. (12, 4)

Ответ: У = 38 П , С = 11 П , Т = 8 П , К = 3 П , М = 6 П ,В = 9 П.

Задание 22 Николай и Витя, гуляя по парку, вышли большую круглую поляну, обсаженную липами. Николай пошел вокруг поляны, считая деревья. Витя сделал то же, но начал с другого дерева. Дерево, которое у Николая было 20-м, у Вите было 7-м, а 7-е — 94-м. Сколько деревьев росло вокруг поляны?

Решение . Рассмотрим нумерацию деревьев в случае, когда ребята двигались в противоположных направлениях (нижняя строка таблицы заполнена справа налево).

20 ≠ 94. Следовательно, ребята двигались в одном направлении, а деревья нумеровали таким образом (нижняя строка таблицы заполнена с обеих сторон):

Ответ: 100 деревьев.

Задание 23. Порвана книга. Из книги выпал кусок. Первая страница куска имеет номер 387, а номер последней состоит из тех же цифр, но записанных в другом порядке. Сколько страниц выпало из книги?

Решение . Номер последней страницы должен быть больше 387 и четным. Итак, этот номер 738. Выпало 738 – 387 + 1 = 352 страниц или 352 : 2 = 176 листов

Ответ: 352 страниц.

Задание 24 . Учитель задал на уроке хитроумную задачу. Количество ребят, решивших эту задачу, совпадает с количеством девушек, которые ее не решили. Кого в классе больше: тех, кто решил задачу или девушек?

Решение . Введем следующие величины:
Х ₊— количество мальчиков, решивших задачу;
Х _– — количество мальчиков, не решивших задачу;
Д ₊ — девушки, решившие задачу;
Д _– девушки, которые не решили задачу.

Есть:
Х ₊ = Д _– — согласно условию задачи;
Х ₊₊ Д + _— количество тех, кто решил задачу;
Д _– + Д ₊ – количество девушек.
Последние две величины совпадают, потому что Х ₊ = Д _– .

Ответ: количества одинаковы.

Задание 25. Десять человек пришли в гости в галошах. Шли назад они по одному, и каждый обовал произвольную пару галош, в которую он мог влезть (т.е. не меньшего размера, чем его собственный). Какое наибольшее количество людей, которые не смогли обуть галоши?

Решение . Занумеруем людей натуральными числами от 1 до 10 в порядке возрастания размера обуви. Рассмотрим такой порядок и способ обува, при котором после каждого шага максимально уменьшается выбор: первый обует галоши 10-го, 2-й — 9-го, 3-й — 8-го, 4-й — 7-го, 5-й. -й – 6-го. При этом без галош останется 5 человек.

Ответ: 5.

Задание 26. Прилетели галки, сели на палки. Если на каждой палке сядет по галке, то для одной галки не хватит палки. Если на каждой палке сядет по две галки, то одна из палок будет без галок. Сколько было палок и сколько было галок?

Решение . Обозначим через Г количество галок, через П – количество палок. Есть:
Г = П + 1 = 2( П – 1) = 2 П – 2, откуда П = 3, Г = 4.

Ответ: 3 палки и 4 галки.

Задание 27. Четыре близнеца - Петр, Николай, Борис и Василий - праздновали свой день рождения. Им подарили коробку конфет. Договорившись разделить конфеты поровну, ребята пошли играть с гостями. Николай вошел в комнату первым, взял свою часть и ушел. Через некоторое время в комнату вошел Петр, взял четвертую часть конфет и ушел. То же сделали Борис и Василий, после чего в коробке осталась 81 конфета. Сколько всего в коробке было конфет и сколько конфет взял каждый из близнецов? Кто и сколько конфет должно взять еще?

Решение . Обозначим через x начальное количество конфет. После действия каждого парня осталось 3/4 количества конфет. Есть:

x · (3/4) · (3/4) · (3/4) · (3/4) = 81,
x · (3 · 3 · 3 · 3)/(4 · 4 · 4 · 4) = 81,
x · 81/256 = 81,
x /256 = 1,
x = 256.

Ответ: x /4 = 64 – количество конфет, которые должен был взять каждый из братьев;
Николай взял 256/4=64 (конфеты), ему не надо ничего брать;
Петр взял 256 – 64/4 = 192/4 = 48 (конфет), ему нужно взять 64 – 48 = 16 (конфет);
Борис взял 192 – 48 / 4 = 144 / 4 = 36 (конфет), ему нужно взять 64 – 36 = 28 (конфет);
Вася взял 144 – 36/4 = 108/4 = 27 (конфет), ему нужно взять 64 – 27 = 37 (конфет).

Задание 28 . В трех ящиках насыпана крупа, вермишель и сахар. На первом ящике написано «крупа», на втором – «вермишель», на третьем – «крупа или сахар». Что в какой ящик насыпано, если содержимое каждого ящика не соответствует надписи на нем?

Решение. Составим прямоугольную таблицу, в которой назовем строки номерами ящиков, а столбцы – (возможным) содержимым. В этой таблице обозначим плюсами или минусами без индексов непосредственные последствия простых предложений условия: «+», если в ящике это есть, иначе – «–». Заполним эту таблицу, исходя из того, что в каждой строке и в каждом столбце должен быть один и только один плюс, а остальные минусы. Индексом справа укажем номер логического шага.

Ответ: в ящике 1 – сахар, в ящике 2 – крупа, в ящике 3 – вермишель.

Задание 29 . На доске написано 1*2*3*4*5*6*7*8 = 20. Вместо символа «*» на доске в неизвестном порядке можно написать символы «+» или «–». Докажите, что равенство не может сбываться.

Ответ:
1 – 2 + 3 + 4 + 5 – 6 + 7 + 8 =
1 + 2 – 3 + 4 – 5 + 6 + 7 + 8 =
1 + 2 + 3 + 4 + 5 + 6 + 7 – 8 = 20
- доказать невозможно, потому что есть 3 контрпримера. Если 20 заменить на произвольное нечетное число, то доводку можно построить на рассуждении, что левая часть равенства всегда четна.

Задание 30 . В таблице 4×4 расставить 7 звездочек таким образом, чтобы при вычерчивании произвольных двух строк и произвольных двух столбиков в остальных клетках была хотя бы одна звездочка.

Решение . Нужно получить такое расположение звездочек, чтобы после вычеркивания двух столбиков звездочки были в трех разных строках:

Ответ: см. расположение, представленное выше. Остальные можно получить с помощью перестановок строк и столбцов.

Задание 31 . 16 слив разложили на столе так, как показано на рисунке ниже.

* * * *
* * * * *
* * * *
* * * *

Затем 6 слив съели, при этом в каждой строке и в каждом столбце остались парные количества слив. Нарисуйте, как лежат оставшиеся сливы.

Решение. С каждой строчки и из каждого столбика взять парное количество слив. Существует строка из которой не брали ни одной сливы, иначе забрали бы не менее 8-ми слив. Аналогично существует столбик, из которого не брали никакой сливы. Из четырех строк четырьмя способами можно выбрать 1 строку, заполненную сливами. Из четырех столбиков четырьмя способами можно выбрать 1 столбик заполненный сливами. В выбранной строке и столбце будет расположено 7 слив. Остаются 3 строки и 3 столбика, которые будут содержать по 1-й сливе. Свободных слив останется 3. Каждую из них нужно расположить в 1-м из трех столбиков. Это можно сделать следующим количеством способов: 3·2·1=6. Следовательно, количество всех способов равно: 4·4·6=96 .

Ответ: существует 96 таких расположений. К примеру, такие.

· · * *
· * · *
* · · *
* * * *


· · * *
· * · *
* * * *
* · · *

Задание 32 . На шахматную доску пролили краску. Может ли количество заляпанных клеток быть на 17 меньше количества чистых клеток?

Решение . Докажем невозможность от противного. Предположим, что это возможно. Обозначим через x количество заляпанных клеток, тогда количество незаляпанных клеток равно x  + 17, а общее количество - 2 x  + 17 = 64. Слева - нечетное число, а справа - четное. Полученное противоречие свидетельствует о ложности противоречия.

Ответ: невозможно.

Задание 33 . Можно ли отмерить 8 литров воды, находясь у ручья с двумя ведрами емкостью 15 литров и 16 литров?

Решение. Приведем таблицей данные о наполнении ведер после наполнений ведра емкостью 16 литров и последующих переливаний.

Ответ: возможно, например, согласно представленной выше схеме переливаний.

Задание 34 . Расставьте числа 1, 1, 2, 2, 3, 3, 4, 4 в таком порядке, чтобы между единицами была одна цифра, между двойками – две, между тройками – три, а между четверками – четыре цифры.

Ответ: 41312432 или 23421314.

Задание 35 . Два мальчика катались на лодке. К берегу подошел отряд солдат. Лодка так мала, что ею могут переправиться два парня или только один солдат. Могут ли солдаты переправиться через реку?

Решение . Опишем процесс переправы одного солдата.

1.                 Ребята, лодка и солдат - на берегу, с которого переправляется.

2.                 Ребята — на разных берегах, солдат и лодка — на берегу с которой переправляется.

3.                 Ребята на разных берегах реки, солдат и лодка — на берегу, на которую переправляется.

4.                 Ребята и лодка — на берегу с которой произведена переправа, солдат — на другом берегу.

Таким образом, солдат можно переправить один за другим.

Ответ: переправа возможна.

Задание 36 . На кольцевой дороге производят эстафету мотоциклистов. Линии старта и финиша эстафеты совпадают. Мотоциклисты двигаются кругом в одном направлении. Длина круга 350 км. Длина каждого этапа 75 км. Какое наименьшее количество этапов может находиться в этой эстафете?

Решение . Искомое количество x удовлетворяет условию: 75 x кратное 350.
1 способ: 75 = 3 · 5 ² , 350 = 2 · 5 ² · 7, откуда x = 2 · 7 = 14.
2 способ:

Ответ: 14 этапов, которые составят 3 полных круга.

Задание 37 . Разделите данную фигуру на 9 одинаковых фигур.

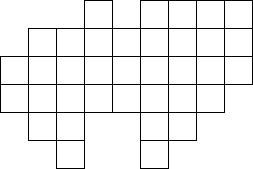
Ответ:

Задание 38 . Машина едет с постоянной скоростью 60 км/ч. На сколько нужно увеличить скорость, чтобы выиграть по одной минуте на каждом пройденном километре?

Решение . Машина проезжает 1 км в 1 мин. Если она будет выигрывать 1 мин в 1 км, то должен преодолевать этот километр мгновенно, что невозможно с физической точки зрения. Если бы ее скорость была меньше (например, при скорости 30 км/ч машина проезжает 1 км в 2 мин), то это было бы возможно (прирост скорости составит 30 км/ч для такой же начальной скорости).

Ответ: это невозможно.

Задание 39 . Анна, Борис, Вера и Гена поймали вместе 10 рыб и все разное количество. Анна поймала больше всех, а Вера меньше всех. Кто поймал больше рыб: мальчики или девочки?

Решение. 1 + 2 + 3 + 4 = 10, поэтому дети выловили следующие количества рыб: 1, 2, 3, 4. Девушки выловили 1 + 4 = 5 (рыбий), а парни - 2 + 3 = 5 (рыбий).

Ответ: количества одинаковы.

Задание 40 . Какая цифра в равенстве 9А : 1А = А заменена буквой А? Здесь в левой части равенства записано отношение двух двухзначных чисел.

Решение . Рассмотрим, сбываются ли равенство для каждого значения отличного от 0 цифры.

Ответ: А = 6.

Задание 41 . Каждый удар силач Бамбула разбивает кусок гранита на 4 части. На сколько кусков он расколол гранитную глыбу, если совершил 666 ударов?

Решение . При каждом ударе количество кусков увеличивается на 3. Искомое количество равно 1+666·3=1999 .

Ответ: 1999 кусков.

Задание 42 . В магическом квадрате сумма чисел в каждой строке, столбце и на диагонали одна и та же. Найдите число N , если известна только часть чисел этого волшебного квадрата.

Решение . 10 + 9 + 14 = 33 – сумма во всех строках, столбцах и на диагонали. Заполним квадрат, указав для каждого числа индексом справа снизу номер логического шага.

Ответ: N = 17.

Задание 43 . По кругу расположено 9 шестерен так, что первая шестерня сцеплена со второй, вторая – с третьей и т.д., а девятая – с первой. Могут ли эти шестеренки вращаться?

Решение . Рассмотрим случай, когда последняя шестерня не совмещена с первой. Будем вращать первую шестерню в направлении часовой стрелки. Две сцепленные шестерни вращаются в противоположных направлениях. Шестерни с нечетным номером будут вращаться по часовой стрелке. Шестерни с парными номерами будут вращаться против направления часовой стрелки. После сцепления первой шестерни с девятой движение станет невозможным.

Ответ: шестеренки не могут вращаться.

Задание 44. Из пунктов А и В одновременно навстречу друг другу вышли два мальчика, каждый со своей, но постоянной скоростью, и встретились через час. После этого они не останавливаясь пошли дальше и, дойдя до пунктов В и А, вернули обратно. Сколько времени пройдет между первой и второй встречами?

Решение . Рассмотрим случай, когда ребята встретились во второй раз после того, как каждый из них изменил направление движения. Расстояние между пунктами ребята проходят вместе через один час. Между встречами им нужно пройти удвоенное расстояние между пунктами через 2 часа.

Если отношение большей скорости к меньшей скорости равно 2, то впервые они встретятся в точке, разделяющей отрезок АВ в отношении 1 : 2 (или 2 : 1), а во второй раз — в пункте B (или А). И как раз через 2 часа.

AC : BC = 1 : 2 =(AC + AB) : BC

Если отношение скоростей ребят превышает 2, ребята встретятся вторично после того, как один из них изменил направление движения, а другой нет. Чем больше отношение скоростей, тем меньшее расстояние между точками встречи и время на их преодоление.

Ответ: не больше 2 часов.

Задание 45 . Сумма девяти разных натуральных чисел равна 46. Какие это числа?

Решение . Сумма девяти наименьших разных натуральных чисел равна:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. Чтобы получить ответ, нужно в одно из этих чисел добавить единицу без нарушения условия, что все числа разные .

Ответ: 1, 2, 3, 4, 5, 6, 7, 8, 10.

Задания 46 . Если четырехзначное число Nразделить на 2 или на 9, то в каждом случае получат трехзначное число, записанное тремя одинаковыми цифрами. Найдите число N.

Решение . Согласно условию задачи существуют следующие цифры x и у , при которых:
N = 2 · x · 111 = 9 · у · 111, откуда 2 · x = 9 · у . Правая и левая части последнего равенства кратны 9. Поэтому x  = 9, у  = 2, N  = 2 · 999 = 1998.

Ответ: N = 1998.

Задание 47. Дорогу протяженностью 28 км разделили на три неровные части. Расстояние между серединами крайних частей равняется 16 км. Найдите длину средней части.

Решение . Обозначим через А, В, С длины участков, А+В+С =28 (км).

Имеем:
А /2+ В /2+ В /2+ С /2=16;
( А+В+С+В ): 2 = 16;
28+ В =16·2=32;
В = 32 – 28 = 4.

Ответ: 4 километра.

Задание 48 . Олекса задумал число. Он прибавил к нему 5, затем разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число задумал Олекса?

Решение . Выполним обратные действия в обратном порядке с конечным результатом:
(2 · 7 + 6) : 4 · 3 – 5 = (14 + 6) : 4 · 3 – 5 = 20 : 4 · 3 – 5 = 5 · 3 – 5 = 15 – 5 = 10.

Ответ: 10.

Задание 50. Белый медведь вышел на прогулку с Северного полюса. Он прошел 10 км к югу, затем – 10 км к востоку, а затем – 10 км к северу. На каком расстоянии от Северного полюса он оказался?

Решение . Движение к востоку или западу является движением вдоль параллели и не изменяет расстояния до полюсов.

Ответ: 0 километров.

Задание 51 . Вдоль изгороди растут 8 кустов малины. Число ягод на соседних кустах отличается на 1. Может ли на всех кустах вместе быть 2013 год ягод?

Решение . Если числа отличаются на 1, то они разной четности. Из 8-ми чисел – количеств ягод на кустах малины – 4 парных и 4 нечетных. Сумма таких чисел парная и не может равняться 2013 году .

Ответ: общее количество ягод отличное от 2013 года.

Задание 51 . Домовой Нафаня купил тетрадь объемом 96 листов и занумеровал все ее страницы по порядку от 1 до 192. Домовой Кузя вырвал из этой тетради 25 листов и добавил все 50 чисел, которые на них написаны. Могло ли у него получиться число 2012 года?

Решение . Из 50 последовательных натуральных чисел 25 четных и 25 нечетных. Сумма таких чисел нечетная и поэтому отлична от 2012 года.

Ответ: сумма номеров страниц отличная от 2012 года.