Министерство образования Самарской области

государственное автономное профессиональное образовательное учреждение Самарской области

«ТОЛЬЯТТИНСКИЙ МАШИНОСТРОИТЕЛЬНЫЙ  КОЛЛЕДЖ»     

сборник методических указаний для ОБУЧАЮЩИХСЯ

 по выполнению ПРАКТИЧЕСКИХ работ

НА ПРАКТИЧЕСКИХ ЗАНЯТИЯХ

МДК 02.03 МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

программы подготовки специалистов среднего звена

09.02.07 Информационные системы и программирование

Тольятти, 2024

Составители:

Игнатьева Е.С. преподаватель ГАПОУ СО «ТМК»,

Рожнова Г.И. преподаватель ГАПОУ СО «ТМК».

Сборник методических указаний для обучающихся по выполнению практических работ на практических занятиях является частью программы подготовки специалистов среднего звена ГАПОУ СО «ТМК» по специальности 09.02.07 Информационные системы и программирование в соответствии с требованиями  ФГОС СПО.

Сборник методических указаний по выполнению практических работ адресован  обучающимся очной формы обучения при изучении МДК 02.03 Математическое моделирование.

Настоящий сборник методических указаний включает в себя пояснительную записку, рекомендации по оформлению отчётов по выполняемым практическим работам, непосредственно методические указания по выполнению каждой работы в соответствии с рабочей программой МДК 02.03 Математическое моделирование.

1.      Пояснительная записка

Методические указания к выполнению практических занятий по МДК 02.03 Математическое моделирование предназначены для закрепления теоретических знаний, полученных на лекциях, а также для овладения обучающимися умений и навыков применять эти знания при самостоятельной работе.

Перечень практических занятий соответствует рабочей программе по МДК 02.03 Математическое моделирование.

Методические указания выполняют функцию управления самостоятельной работой обучающегося, поэтому каждое занятие имеет унифицированную структуру, включающую определение целей занятия, оборудования занятия, порядок выполнения работы, а также задания и контрольные вопросы для закрепления темы.

В результате освоения МДК обучающийся должен иметь практический опыт:

В результате освоения учебной дисциплины обучающийся должен уметь:

В результате освоения учебной дисциплины обучающийся должен знать:

2.             Введение

Уважаемый обучающийся!

Методические указания по МДК 02.03 Математическое моделирование для выполнения практических  работ созданы Вам  в помощь для работы на занятиях, подготовки к практическим  работам, правильного составления отчетов.

         Приступая, к выполнению практической работы Вы должны внимательно прочитать тему и  цель занятия, пояснениями к работе (учебный материал), ответить на вопросы для закрепления теоретического материала.

         Все задания к практической работе Вы должны выполнять в соответствии с инструкцией, анализировать полученные в ходе занятия результаты по приведенной методике.

         Отчет о практической работе Вы должны выполнить по приведенному алгоритму, опираясь на образец.

         Наличие положительной оценки по практическим работам необходимо для получения зачета по дисциплине, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной оценки за практическую работу Вы должны найти время для ее выполнения или пересдачи.

Внимание! Если в процессе подготовки к практическим работам или при решении задач у Вас возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий.

         Время проведения дополнительных занятий можно узнать у преподавателя или посмотреть на двери его кабинета.

                   Нормы оценки знаний, умений и навыков обучающихся

                   Оценка практических работ обучающихся

Ответ оценивается отметкой «5», если:

-              работа выполнена полностью;

-              в логических рассуждениях и обосновании решения нет пробелов и ошибок;

-              в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

 Отметка «4» ставится в следующих случаях:

-              работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

-              допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

-              допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

-              допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Преподаватель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Тема практической работы №1:

Построение простейших математических моделей. Построение простейших статистических моделей

Цель работы: 

- закрепить практические навыки по построению простейших математических и простейших статистических моделей.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

1 вариант.

Задача 1.

Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В.

а1= 19, а2= 16, а3= 19, b1= 26, b2= 17, b3= 8, c1= 868, c2= 638, c3= 853, α=5, β=4.

Задача 2.

Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:

Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.

а1=300,  а2=250,  а3=200,

         b1=210,  b2=150,  b3=120,  b4=135,    b5=135.

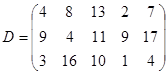
2 вариант.

Задача 1.

Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В.

а1= 14, а2= 15, а3= 20, b1= 40, b2= 27, b3= 4, c1= 1200, c2= 993, c3= 1097, α=5, β=13.

Задача 2.

Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:

Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.

        а1=350,  а2=200,  а3=300,

        b1=170,  b2=140,  b3=200,  b4=195,      b5=145.

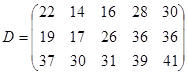
Порядок выполнения:

1.    Внимательно прочитать тему и цель практической работы.

2.    Изучить учебный материал по теме.

3.    Ответить на вопросы.

4.    Выполнить задания.

5.    Подготовить отчет

Пояснения к работе (учебный материал):

Построение математической модели процесса, явления или объекта начинается с построения упрощенного варианта модели, в котором учитываются только основные черты. В результате прослеживаются основные связи между входными параметрами, ограничениями и показателем эффективности. Общего подхода к построению модели нет. В каждом конкретном случае при построении математической модели учитывается большое количество факторов: цель построения модели, круг решаемых задач, точность описания модели и точность выполнения вычислений. Математическая модель должна отражать все существенные факторы, определяющие ее поведение, и при этом быть простой и удобной для восприятия результатов. Каждая математическая модель процесса, явления или объекта в своей основе имеет математический количественный метод.

Применение математических количественных методов для обоснования выбора того или иного управляющего решения во всех областях человеческой деятельности называется исследованием операций. Целью исследования операций является нахождение с использованием специального математического аппарата решения, удовлетворяющего заданным условиям. На самом деле при решении практически любой задачи имеется неограниченное количество решений. Множество решений, удовлетворяющих заданным условиям (ограничениям), называется допустимым множеством решением. Выбор из множества допустимых решений одного решения, наилучшего в каком-либо смысле, называемого оптимальным решением, и есть задача исследования операций.

Модель — это материальный или идеальный объект, заменяющий оригинал, наделенный основными характеристиками (чертами) оригинала и предназначенный для проведения некоторых действий над ним с целью получения новых сведений об оригинале.

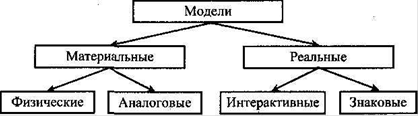
                       Рис. 1. Классификация моделей

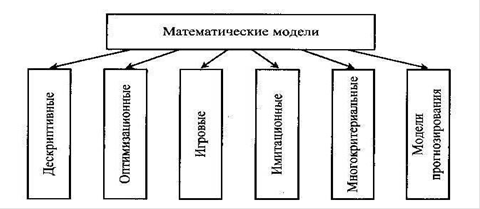
            Рисунок 1. Классификация математических моделей

При построении математической модели необходимо обеспечить достаточную точность вычислений (точность решения) и необходимую подробность модели. Любая математическая модель включает в себя описание основных, т. е. необходимых для исследования свойств и законов функционирования исследуемого объекта, процесса или явления. В своей основе каждая математическая модель имеет целевую функцию, которая описывает функционирование реального объекта, процесса или явления. В зависимости от исследуемого (моделируемого) объекта, явления или процесса целевая функция может быть представлена одной функциональной зависимостью, системой уравнений (линейных, нелинейных, дифференциальных и т. д.), набором статистических данных и т. д. При работе с целевой функцией исследователь воздействует на нее через набор входных параметров (рис. 2).

Рисунок 2. Обобщенная схема математической модели

По способу реализации математические модели можно разделить следующим образом.

1.    Линейное программирование.

Математическая модель целиком (целевая функция и ограничения) описывается уравнениями первого порядка. Линейное программирование включает в себя несколько методов решения (задач):

•       симплексный;

•       графический;

•       транспортная задача;

•       целочисленное программирование.

2.    Нелинейное программирование.

Целевая функция и ограничения, составляющие математическую модель, содержат хотя бы одно нелинейное уравнение (уравнение второго порядка и выше). Нелинейное программирование содержит несколько методов решения (задач):

•       графический;

•       регулярного симплекса;

•       деформируемого многогранника (Нелдера - Мида);

•       градиентный.

3.    Динамическое программирование.

Ориентировано на решение задач прокладки магистралей кратчайшим путем и перераспределения различных видов ресурсов.

4.    Сетевое планирование.

Решает проблему построения графика выполнения работ, распределения производственных, финансовых и людских ресурсов.

5.    Принятие решений и элементы планирования.

В этом случае и качестве целевой функции выступает набор статистических данных или некоторые данные прогноза. Решением задачи являются рекомендации о способах поведения (стратегии). Решение носит рекомендательный характер (приблизительное решение). Выбор стратегии целиком остается за человеком — ответственным лицом, принимающим решение. Для принятия решения разработаны следующие теории:

•  теория игр;

•  системы массового обслуживания

При выполнении практической работы рассмотрите следующие примеры:

Задача 1.

Составить математическую модель следующей задачи. На складе имеется 300 кг сырья. Надо изготовить два вида продукции. На изготовление первого изделия требуется 2 кг сырья, а на изготовление второго изделия — 5 кг. Определить план выпуска двух изделий.

Решение.

Обозначим,

  – единица первого изделия,

 – единица второго изделия.

Тогда составим математическая модель:

Задача 2.

Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал 3-х сортов. При этом на изготовление единицы изделия вида А расходуется 14 кг первого сорта, 12 кг второго сорта и 8 кг третьего сорта. На изготовление продукции вида В расходуется 8 кг первого сорта, 4 кг второго сорта, 2 кг третьего сорта. На складе фабрики имеется всего материала первого сорта 624 кг, второго сорта 541 кг, третьего сорта 376 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида 7 руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида 3 руб. Определить максимальную прибыль от реализации всей продукции видов А и В.

  Решение.

Составим математическую модель задачи:

Пусть  – единица готовой продукции вида А,

 - единица готовой продукции вида В,

Цель фабрики получить максимальную прибыль от реализации всей продукции видов А и В, тогда:

Система ограничений:

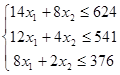
 - условие неотрицательности

Задание 3.

Составить математическую модель следующей задачи. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве 200, 450, 250 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно 100, 125, 325, 250, 100 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:

Решение:

1.    Проверка сбалансированности модели задачи.

Модель является сбалансированной, т.к. суммарный объем запасов сырья равен суммарному объему потребности в ней:

200+450+250=100+125+325+250+100.

2.    Построение математической модели – неизвестными в этой задачи является объем

перевозок.

Пусть - объем перевозок с i-го предприятия в j-го пункт потребления.

Суммарные транспортные расходы - это функционал качества (критерий цели):

,

Где - стоимость перевозки единицы продукции с i-го предприятия в j-й пунктах потребления.

Неизвестные в этой задачи должны удовлетворять следующим ограничениям:

·   Объем перевозок не могут быть отрицательными;

·      Поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятия, а потребность всех пунктов потребления должна быть полностью удовлетворены.

Итак, имеем следующую задачу:

·   Найти минимум функционала:

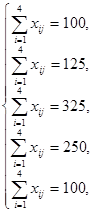
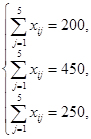
·   При ограничениях:

Вопросы для закрепления теоретического материала к практическому занятию:

1.    Что такое модель? Приведите классификацию моделей. Какие вы знаете виды математических моделей? Дайте определение целевой функции.

2.    Что такое область допустимых решений? Что называется допустимым решением, оптимальным решением? Какие способы реализации математических моделей вы знаете?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    «Исследование операций в экономике» под редакцией профессора Кремера Н.Ш., М: Банки и биржи, 2019

2.    Хазанова Л.Э. «Математическое моделирование в экономике» Учебное пособие, М: Изд. БЕК, 2019г

3.    Конюховский П.В. «Математические методы исследования операций в экономике» Учебное пособие, С-Пб «Питер», 2020

4.    Шикин Е.В., Чхартишвили А.Г. «Математические методы и модели в управлении» М: «Дело» 2018

5.    Бережная Е.В., Бережной В.И. «Математические методы моделирования экономических систем», М: Финансы и статистика, 2018

6.    Солодовников А.С., Бабайцев В.А., Браилов А.В. «Математика в экономике» М: Финансы и статистика» , 2018г., 1 часть

7.    Красс М.С., Чупрынов Б.П.» Основы математики и её приложения в экономическом образовании» М: «Дело», 2002, Раздел 2

8.    Матвеев Л.А. «Компьютерная поддержка решений», Санкт-Петербург «Специальная литература», 2019

9.    Черемухина О.В. Сборник задач по дисциплине «Экономико-математическое моделирование» для студентов очного и заочного отделений экономических специальностей. Уральск 2020г.

10.    Черемухина О.В. Методические указания по теме: «Оптимизация производственных процессов в электронной таблице Excel» для студентов экономических специальностей очного и заочного отделений. Уральск 2005г.

11.    Вентцель Е.С. «Исследование операций» М: «Высшая школа», 2021

12.    Шелобаев С.И. «Математические методы и модели в экономике, финансах и бизнесе», М.: ЮНИТИ,  2020г.

13.    Волгина, О.А., Математическое моделирование экономических процессов и систем : учебное пособие / О.А. Волгина, Г.И. Шуман. — Москва : КноРус, 2022. — 256 с. — ISBN 978-5-406-08869-2. — URL:https://book.ru/book/941747 (дата обращения: 16.01.2022). — Текст : электронный.

Савиных, В.Н., Математическое моделирование производственного и финансового менеджмента : учебное пособие / В.Н. Савиных. — Москва : КноРус, 2020. — 192 с. — ISBN 978-5-406-07823-5. — URL:https://book.ru/book/934057 (дата обращения: 16.01.2022). — Текст : электронный.

Критерии оценки за выполнение практического занятия