Серия уроков геометрии "Построение эллипса, параболы, гиперболы""

Серия уроков геометрии.

ТЕМА: Эллипс, парабола, гипербола.

Цели:

1. Развитие логического мышления и творческих способностей обучающихся.

2. Формирование новых математических знаний.

3. Формирование компетентностного подхода при изучении нового материала.

Задачи:

1.Учащиеся должны понимать, что геометрические формы являются идеализированными образами реальных объектов, получить представление о некоторых областях применения геометрии в быту, науке, технике, искусстве.

2. Учащиеся должны владеть практическими навыками использования инструментов для изображения фигур.

Замечательные геометрические объекты- кривые линии привлекают внимание не только изяществом своей формы, но и многими удивительными свойствами.

Наряду с окружностью заслуженными «старожилами» в математике являются - эллипс, парабола и гипербола.

Эллипс.

1. Иоганн Кеплер – законодатель неба.

-Ученики заранее готовят выступления о жизни и деятельности Кеплера.

-Учитель готовит презентацию с иллюстрацией к первому закону Кеплера: планета Р движется по эллиптической орбите. Эллипс имеет два фокуса, в одном из них находится солнце.  Презентация сопровождается рассказом учителя о том, как Кеплер в 17 веке установил, что все планеты движутся по эллиптической орбите.

2. Практическая работа

а) Ученики уже знакомы с эллипсом и часто его называют овалом. Как правило, они говорят, что овал можно получить, надавив на окружность сверху и снизу.

Учитель рассказывает, что эллипс – это «сплюснутая», а точнее, равномерно сжатая к своему диаметру окружность.

- Класс разбивается на рабочие группы.

У каждой группы на столе лежат лист ватмана, вырезанный из бумаги круг, две кнопки, нитки, карандаш, циркуль.

Группам предлагается из заготовленного круга получить эллипс, обсудив, что значит равномерно сжать к диаметру.

Группы рассказывают о проделанной работе и показывают результаты работы.

б) Иногда хочется украсить сад красивой цветочной клумбой. Почему бы не придать ей необычную эллиптическую форму?

Как имея два колышка (кнопки), верёвку (нитки) и палку (карандаш) вычертить на земле (ватмане) эллипс?

Группам предлагается выполнить построение. Для того чтобы нарисовать эллипс нужно прикрепить концы нитки к двум закреплённым кнопкам, карандашом натянуть нить так, чтобы его острие касалось бумаги. Перемещаем карандаш по бумаге так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать эллипс.

в) Далее работаем над свойствами эллипса:

- Каким свойством обладают точки, лежащие на эллипсе?

Сумма расстояний от точек, лежащих на эллипсе, до двух заданных точек есть величина постоянная.

- Вспомнить понятие ГМТ и дать определение эллипса.

Геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек есть величина постоянная, называется эллипсом.

- Вернуться к презентации и дать «названия» некоторым точкам.

Точки S  и F называются фокусами. Слово focus в переводе с латинского означает «огонь», «очаг». Происхождение этого названия объясняется замечательным оптическим свойством эллипса: прямые, соединяющие любую его точку с фокусами, составляют с касательной к эллипсу в этой точке равные углы. Если представить себе, что эллипс, подобно зеркалу, может отражать световые лучи, и поместить в один из его фокусов источник света, то лучи, отражаясь от эллипса, соберутся в другом фокусе. Так же распространяются и акустические волны, что используют архитекторы для создания поразительных звуковых эффектов: «говорящих» бюстов, «мистического» шёпота, «потусторонних» звуков.

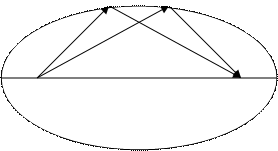
 Точка В орбиты планеты, расположенная ближе к Солнцу, называется перигелием, точка А - наиболее удалённая от Солнц - афелием.

г) Обратимся к искусству.

Леонардо да Винчи предложил для рисования эллипсов замечательный механизм.

Ребятам предстоит знакомство с данной конструкцией. Поможет пример. Котёнок примостился на лестнице, которая скользит по стене. Допустим, что котёнок спрыгнет с неё не сразу. Тогда находясь на лестнице, он опишет в пространстве…? Дугу эллипса. На этом свойстве основано действие механизма.

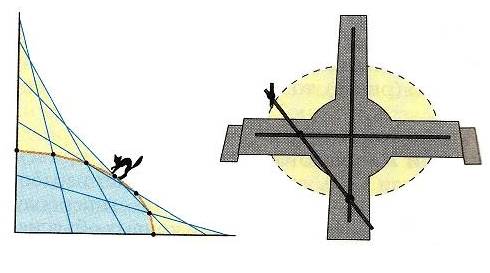
Можно предложить ребятам пофантазировать и выдвинуть свои предложения.  В качестве подсказки могут быть предложены заготовки: изображённые на листе перпендикулярные прямые и произвольный треугольник, вырезанный из плотной бумаги.

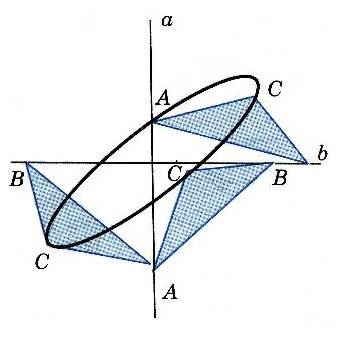
  Леонардо да Винчи предложил интересный способ построения эллипса. Вырежем из бумаги произвольный треугольник АВС. Проведём на листе бумаги две перпендикулярные прямые a и b. Будем прикладывать треугольник АВС так, чтобы вершина А принадлежала прямой a, вершина В – прямой b, отмечая всякий раз на бумаге положение вершины С. Различные положения вершины С будут заполнять эллипс.

д) Сковородка в помощь.

(Это может быть домашнее задание)

Как, используя сковороду и круг диаметром вдвое меньше диаметра сковороды получить эллипс?

  Клейкой лентой укрепить на дне сковородки лист бумаги. Положив круг на сковороду, продырявьте его в любом месте, отличном от центра, отточенным карандашом. Если теперь катить круг по краю сковороды, прижимая острие карандаша к бумаге, то карандаш будет описывать эллипс.

е) Касательная к эллипсу.

Касательной к эллипсу называется прямая, имеющая с эллипсом только одну общую точку.

Вырежьте из бумаги круг и в любом его месте, отличном от центра, поставьте точку. Сложите круг так, чтобы эта точка совместилась с какой-нибудь точкой окружности круга  и на бумаге образовалась линия сгиба. Разогните круг и снова согните его, совместив точку с другой точкой окружности круга. Сделайте так несколько раз, пока вся бумага не покроется линиями сгибов. Участок круга внутри этих сгибов будет иметь форму эллипса. Покажите, что линии сгибов будут касательными.

ж) Задания.

1. Даны фокусы эллипса и сумма расстояний до них. С помощью циркуля постройте несколько точек этого эллипса.

2. Для заданных точек А и В найдите геометрическое место точек С, для которых периметр треугольника АВС равен постоянной величине с.

3. Найдите геометрическое место точек пересечения пар окружностей с заданными центрами и суммой радиусов.  

Парабола.

1.Выступления учащихся.

Учащиеся готовят выступления с помощью учителей математики и физики об оптических свойствах, на которых основано действие фар, рефлекторов, антенн радиотелескопов, карманных фонариков.

Любой луч света, исходящий из фокуса, после отражения от параболы становится параллельным оси параболы.

Если источник света помещён в фокусе параболы, то фронт отражённой от параболы волны представляет собой отрезок, соединяющий две точки параболы и параллельный её директрисе.

2. Рисуем параболу.

Даём определение параболы. Пусть на плоскости задана прямая  d и точка F, не лежащая на данной прямой. Геометрическое место точек, равноудалённых от прямой d и точки F, называется параболой. Прямая d называется директрисой, а точка F – фокусом параболы.

- Задание.

 Как с помощью имеющихся инструментов начертить параболу?

У ребят имеются линейка, угольник, нить длиной, равной большему катету угольника, и кнопки.

  Для того чтобы нарисовать параболу, необходимо один конец нити прикрепить к фокусу, а другой – к вершине меньшего угла угольника. Приложим линейку к директрисе и поставим на неё угольник меньшим катетом. Карандашом натянем нить так, чтобы его острие касалось бумаги и прижималось к большему катету. Будем перемещать угольник и прижимать к его катету карандаш так, чтобы нить оставалась натянутой. Карандаш будет вычерчивать параболу.

3. Даём названия.

Осью параболы называется прямая, проходящая через фокус и перпендикулярная директрисе.

Точка пересечения параболы с её осью называется вершиной параболы.

Прямая, имеющая с параболой только одну общую точку и не перпендикулярная к директрисе, называется касательной к параболе.

4. Практическая работа.

Возьмите лист бумаги прямоугольной формы и отметьте около его большей стороны точку S. Сложите лист так, чтобы точка S совместилась с какой-нибудь точкой на большей стороне. Разогните лист и снова согните его, совместив точку S с другой точкой большей стороны. Сделайте так несколько раз, пока вся бумага не покроется линиями сгибов. Участок внутри этих сгибов будет иметь форму параболы. Линии сгибов являются касательными к параболе.

Данную работу можно предложить учащимся выполнить в парах самостоятельн

5. Задания.

1) Для заданных фокуса и директрисы параболы с помощью циркуля и линейки постройте несколько точек параболы

2) Для параболы с заданным фокусом и директрисой проведите касательную, перпендикулярную оси параболе.

Гипербола.

1.                  Чертим неизвестный геометрический объект.

Для того чтобы нарисовать гиперболу, потребуется линейка, нить, длина которой меньше длины линейки, а разность длин линейки и нити должна быть меньше, чем расстояние между фокусами.

Прикрепим один конец нити к концу линейки, а другой конец к фокусу (кнопке). Второй конец линейки совместим со вторым фокусом (кнопкой). Натянем нить, прижав её к линейке острием карандаша. Если поворачивать линейку вокруг фокуса, прижимая к ней карандаш и оставляя нить натянутой, то карандаш будет описывать гиперболу.

2.                  Учащиеся устанавливают свойства объекта и дают ему определение.

Имея определённые навыки, ребята должны попытаться дать определение объекту. Учитель корректирует в случае необходимости и даёт название.

Геометрическое место точек плоскости, модуль разности от которых до двух заданных точек Fи Fравен фиксированному положительному числу, называется гиперболой. Точки F и F называются фокусами гиперболы.

3.                  Практическая работа.

Вырежьте из листа бумаги круг и отметьте точку на оставшейся части листа. Сложите лист так, чтобы эта точка совместилась с какой-нибудь точкой окружности вырезанного круга и на бумаге образовалась линия сгиба. Разогните лист и снова согните его, совместив точку с другой точкой окружности. Сделайте так несколько раз. Участок листа внутри этих сгибов будет иметь форму гиперболы. Линии сгибов будут касательными.

Обобщение материала.

Учащиеся в группах или в парах пытаются обобщить изученный материал.

- Любая из трёх линий - парабола, гипербола и эллипс - есть множество всех точек, для каждой из которых отношение расстояния до данной точки, называемой фокусом, к расстоянию до данной прямой, называемой директрисой и не проходящей через фокус, равно одному и тому же положительному числу, которое равно1 в случае параболы, больше единицы в случае гиперболы и меньше единицы в случае эллипса.

Вопрос к учащимся: знаем ли мы, какая прямая или прямые являются директрисой для эллипса и гиперболы?

- Учащиеся выдвигают свои предположения.

Каждому фокусу эллипса и также гиперболы соответствует такая прямая, что отношение расстояния от любой точки эллипса или гиперболы до фокуса к расстоянию от этой точки до соответствующей прямой имеет одно и тоже значение. Таких прямых две, они называются директрисами эллипса или гиперболы.

- Интересный факт. Возьмём на плоскости две точки и рассмотрим всевозможные эллипсы и гиперболы, для которых эти точки являются фокусами. Оказывается, что каждая из этих гипербол пересекается с каждым эллипсом под прямым углом, т. е. угол между касательными к гиперболе и эллипсу, проведенными через точку гиперболы и эллипса, равен 90 градусов.

- Парабола, гипербола и эллипс встречаются в самых разнообразных ситуациях. Так, ближний свет автомобильной фары освещает часть асфальта, ограниченную эллипсом, а дальний – гиперболой. Брошенный камен движется по параболе, а движение небесных тел (планет, комет, метеоритов и т.д.) под действием притяжения Солнца происходит по эллипсу или гиперболе. Конечно, небесные тела испытывают воздействие не только Солнца, но и других тел, и поэтому их истинные траектории не являются в точности гиперболой или эллипсоидом, но весьма близки к этим линиям. Так, каждая планета Солнечной системы, в том числе наша Земля, движется по орбите, близкой к эллиптической, причём Солнце находится в одном из фокусов эллипса. 

Список литературы:

1)      Смирнова И.М. Геометрия 7-8.-Москва: Просвещение, 2001.

2)      Атанасян Л.С. Геометрия. Дополнительные главы к школьному учебнику 9 класса. –Моска: Просвещение, 1997.

3)      Энциклопедия для детей. Т.11. Математика. –Москва: Аванта+, 2000.

4)      Энциклопедия для детей. Т.8. Астрономия. –Москва: Аванта+, 2002.

5)