Поделиться
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ.docx
системы линейных уравнений с двумя переменными
Цели: ввести понятие системы уравнений с двумя переменными; формировать умение решать графически системы линейных уравнений с двумя переменными.
Ход урока
I. Устная работа.
1. Какие из пар чисел являются решениями уравнения –х – у = 5?
а) (2; 3); б) (–2; 3); в) (–3; –2); г) (1; –6).
2. Даны два уравнения: х + у = 3 и х – у = 1. Какие из пар чисел являются одновременно решением каждого из этих уравнений:
а) (1; 2); б) (–1; 2); в) (2; 1); г) (–2; 5)?
II. Объяснение нового материала.
Ввести понятие системы уравнений с двумя переменными и рассмотреть, как графически решаются системы линейных уравнений.
1. Рассмотреть задачу из учебника, подводящую к понятию системы уравнений с двумя переменными. Здесь необходимо добиться чёткого понимания учащимися того, в чём состоит отличие простых уравнений с двумя переменными от их систем.
2. Ввести понятие решения системы уравнений с двумя переменными. Желательно привести примеры, показывающие, что некоторые пары чисел могут быть решением какого-либо одного уравнения системы, но не являться решением всей системы.
Пример.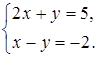 
|
(2; 1) – |
является решением 1-го
уравнения системы, но не является решением 2-го, значит, не является решением
системы |
|
(–1; 1) – |
является решением 2-го
уравнения системы, но не является решением 1-го, значит, не является решением
системы |
|
(1; 3) – |
является решением и 1-го, и
2-го уравнений, значит, |
III. Формирование умений и навыков.
1. № 1056.
Необходимо показать учащимся, как следует оформлять решение подобных заданий:
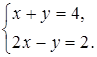
а) х = 3, у = 1: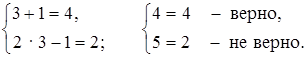 
Ответ: не является.
б) х = 2, у = 2: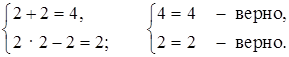 
Ответ: является.
2. № 1058 (а).
3. № 1059. Например:
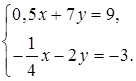
4. № 1060 (а, б).
IV. Итоги урока.
Домашнее задание: № 1057; № 1058 (б); № 1060 (в, г)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
