Системы счисления, используемые в ЭВМ

Системы счисления, используемые в ЭВМ

Очевидно, число «десять» — не единственно возможное основание позиционной системы. Известный русский мате­матик Н.Н.Лузин так выразился по этому поводу: «Пре­имущества десятичной системы не математические, а зоо­логические. Если бы у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой».

За основание позиционной системы счисления можно принять любое натуральное число большее 1. Упомянутая выше вавилонская система имела основание 60. Следы этой системы сохранились до наших дней в порядке счета единиц времени (1 час = 60 мин, 1 мин = 60 с).

Для записи чисел в позиционной системе с основанием n нужно иметь алфавитиз n цифр. Обычно для этого при n<10 используют n первых арабских цифр, а при n>10 к десяти арабским цифрам добавляют буквы.

Вот примеры алфавитов нескольких систем:

Основание системы, к которой относится число, обозначается подстрочным индексом к этому числу.                                                                                           

101101₂, 3671₈, 3B8F₁₆.

.

Принципы архитектуры ЭВМ были сформулированы Джоном фон Нейманом в 1946 году. Им долгие годы сле­довали конструкторы ЭВМ. Многие из этих принципов со­хранились и в архитектуре современных компьютеров.

Один из этих принципов Неймана:

ЭВМ выполняет арифметические расчеты в двоичной системе счисления.

Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

·         для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

·         представление информации посредством только двух состояний надежно и помехоустойчиво;

·         возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

·         двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Гораздо проще сконструировать процессор, который ра­ботает в двоичной системе счисления, чем работающий в десятичной. Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

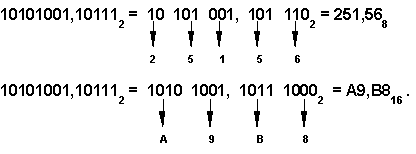
Шестнадцатеричная система счисления используется для компактного представления (на бумаге или на экране) двоичной информации, хранимой в памяти ЭВМ.