СОЗДАНИЕ АЛГОРИТМА.docx

СОЗДАНИЕ АЛГОРИТМА

Разработка программы состоит из двух различных действий – создания алгоритма ее работы и представления этого ал- горитма в виде программы. До настоящего момента мы рассматривали только способы представления алгоритмов и не каса- лись вопроса, как, собственно, эти алгоритмы создаются. Однако создание алгоритма – это, как правило, наиболее сложный этап в процессе разработки программного обеспечения. В конце концов, создать алгоритм – означает найти метод решения задачи, в решении которой и состоит назначение этого алгоритма. Поэтому, чтобы понять, как создаются алгоритмы, необ- ходимо понять процесс решения задач.

Теория решения задач. Рассмотрение методов решения задач и их подробное изучение не являются аспектами, специ- фическими только для компьютерных наук. Напротив, это важно практически для любой области науки. Тесная связь между процессом создания алгоритмов и общей проблемой поиска решения задач привела к сотрудничеству специалистов в облас- ти компьютерных систем и ученых из других областей науки в поисках лучших методов решения задач. В конечном счете, желательно было бы свести проблему решения задач к алгоритмам как таковым, но это оказалось невозможным. (В главе 11 будет показано, что существуют задачи, не имеющие алгоритмических решений.) Таким образом, способность решать зада- чи в значительной степени является профессиональным навыком, который необходимо развивать, а не точной наукой, кото- рую можно изучить.

Решение задач является скорее искусством, чем наукой. Доказательством этого может служить тот факт, что представ- ленные ниже, весьма расплывчато определенные фазы решения задач, предложенные математиком Дж. Полиа (G. Polya) в 1945 г., остаются теми основными принципами, на которых и сегодня базируется обучение навыкам решения задач.

Фаза 1. Понять существо задачи.

Фаза 2. Разработать план решения задачи.

Фаза 3. Выполнить план.

Фаза 4. Оценить точность решения, а также его потенциал в качестве средства для решения других задач. Применительно к процессу разработки программ эти фазы выглядят следующим образом.

Фаза 1. Понять существо задачи.

Фаза 2. Предложить идею, какая алгоритмическая процедура позволяет решить задачу.

Фаза 3. Сформулировать алгоритм и представить его в виде программы.

Фаза 4. Оценить точность программы и ее потенциал в качестве средства для решения других задач.

Необходимо подчеркнуть, что предложенные математиком Полиа фазы не являются этапами, которым надо следовать при решении задачи. Скорее, это те фазы, которые должны быть когда-либо выполнены в процессе ее решения. Здесь ключе- вое слово – следовать, т.е. просто "следуя", вы не сможете решить задачу. Напротив, чтобы решить задачу, необходимо про- являть инициативу и двигаться вперед. Если подходить к решению задачи по принципу: "Ну вот, я закончил фазу 1, пора переходить к фазе 2", то вряд ли вам будет сопутствовать успех. Однако если вы с головой окунетесь в решение задачи и, в конечном счете, решите ее, то, оглянувшись назад, обязательно увидите, что выполнили все четыре фазы, предложенные математиком Полиа.

Кроме того, необходимо заметить, что эти четыре фазы не обязательно выполняются в указанном порядке. Как отмеча- ют многие авторы, те, кто успешно решают задачи, часто начинают формулировать стратегию решения (фаза 2) еще до того, как полностью смогут понять существо задачи (фаза 1). Впоследствии, если выбранные стратегии так и не приведут к успеху (что проявится во время фазы 3 или 4), решающий задачу человек все же приобретет более глубокое понимание сути задачи и, основываясь на этом понимании, сможет вновь вернуться к формулированию других, возможно, более успешных страте- гий.

Не забывайте, что здесь мы обсуждаем, как задачи решаются, а не то, как бы нам хотелось, чтобы они решались. В идеале хотелось бы полностью исключить изнурительный по своей сути процесс проб и ошибок, описанный выше. При раз- работке крупной системы программного обеспечения обнаружение неправильного понимания лишь на фазе 4 может привес- ти к огромным потерям ресурсов. Избежать таких катастроф – основная задача разработчиков программного обеспечения (глава 6), которые традиционно настаивают на том, что полное осмысление задачи должно предшествовать ее решению. Можно возразить, что истинное понимание задачи невозможно, пока не будет найдено ее решение. Тот факт, что решить задачу не удается, подразумевает недостаток ее понимания. Следовательно, настаивать на том, что нужно вначале полно- стью осознать задачу, прежде чем предлагать какое-либо ее решение, – это чистый идеализм. В качестве примера рассмот- рим следующую задачу.

Предположим, что некто А хочет определить возраст трех детей некоего В. Этот В сообща- ет А, что произведение возрастов его детей равно 36. Обдумав эту подсказку, А отвечает, что необходима еще подсказка, и B сообщает ему сумму возрастов его детей. Затем А отвеча- ет, что требуется еще подсказка, и В говорит ему, что старший из детей играет на пианино. Услышав эту подсказку, А сообщает В возраст всех трех его детей. Сколько лет детям?

На первый взгляд может показаться, что последняя подсказка совсем не имеет отношения к задаче, хотя именно она по- зволила А окончательно определить возраст детей. Как это может быть? Давайте двигаться вперед, формулируя план и сле- дуя ему, несмотря на то, что у нас еще остается много вопросов по поводу этой задачи. Наш план будет состоять в том, что- бы отслеживать этапы, описанные в условии задачи, учитывая информацию, доступную А по мере развития событий.

В первой подсказке сообщалось, что произведение возрастов детей равно 36. Это означает, что искомые значения образуют одну из троек, перечисленных на рис. 4.5, а. Следующая подсказка указывала сумму искомых значений. Нам неизвестно, чему именно равна эта сумма, но мы знаем, что этой информации оказалось недостаточно, чтобы А смог выбрать правиль- ную тройку. Следовательно, искомая тройка должна быть одной из тех, которые имеют одинаковые суммы в списке на рис. 4.5, б. Таких троек на рисунке две: (1, 6, 6) и (2, 2, 9); сумма членов каждой из них равна 13. Это та информация, которая бы- ла известна А на момент, когда он получил последнюю подсказку. Именно на данном этапе мы осознаем важность последней подсказки. Собственно умение играть на пианино не имеет никакого значения, важен тот факт, что в семье есть старший ребе- нок. Это позволяет отбросить тройку (1, 6, 6) и заключить, что одному ребенку 9 лет, а двум – по 2 года.

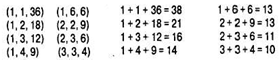а)                                                 б)

Рис. 4.5. Иллюстрация к задаче о трех детях:

а – тройки чисел, произведение которых равно 36;

б – суммы троек чисел, приведенных в а)

Это именно тот случай, когда, не попытавшись реализовать выбранный план решения (фаза 3), невозможно достичь полного понимания задачи (фаза 1). Если бы мы настаивали на завершении фазы 1, вместо того чтобы двигаться дальше, то, возможно, так и не смогли бы определить возраст детей. Такая неупорядоченность процесса решения задач является основ- ной причиной трудностей, связанных с разработкой систематического подхода к решению задач.

Кроме того, существует и некое мистическое вдохновение, посещающее человека, решающего задачу. Оно проявляется в том, что, работая какое-то время над задачей без видимого успеха, позднее он неожиданно может найти ее решение при выполнении совершенно другого задания. Этот феномен был обнаружен ученым Г. фон Гельмгольцем (Н. von Helmholtz) еще в 1896 г., а математик Анри Пуанкаре (Henri. Poincare) говорил о нем в своей лекции, прочитанной Психологическому обществу в Париже. Пуанкаре описал свой опыт, связанный с неожиданным осознанием способа решения задачи, которой он безуспешно занимался некоторое время, а затем отложил, обратившись к другим проблемам. Этот феномен отражает про- цесс, в котором подсознание осуществляет непрерывную работу над решением задачи и в случае успеха выталкивает най- денный результат в сознание человека. В наши дни промежуток времени между процессом сознательного решения задачи и вне- запным озарением получил название инкубационного периода. Исследования этого явления продолжаются и в настоящее время.

Общие методы решения задач. Мы обсудили решение проблем с философской точки зрения, пока не затрагивая во- прос, как следует действовать при попытке решить некоторую задачу. Безусловно, существует множество подходов к реше- нию задач, каждый из которых приводит к успеху в определенных ситуациях. Ниже мы кратко обсудим некоторые из них. Сейчас же просто отметим, что существует нечто общее, присущее всем этим методам. Это можно охарактеризовать как вы- бор оптимальной позиции для дальнейших действий. В качестве примера рассмотрим следующую простую задачу.

Перед соревнованиями участники А, В, С и D сделали следующие прогнозы: Участник А предсказал, что победит участник В.

Участник В предсказал, что участник D будет последним. Участник С предсказал, что участник А будет третьим.

Участник D предсказал, что сбудется предсказание участника А.

Только один из этих прогнозов оказался верным, и это был прогноз победителя.

В каком порядке участники А, В, С и D закончили соревнования?

Ознакомившись с задачей и проанализировав приведенные в ее условии сведения, нетрудно заметить, что, поскольку прогнозы участников А и D эквивалентны, а верным оказался только один прогноз, прогнозы участников А и D неверны. Следовательно, ни участник А, ни участник D не являются победителями соревнования. Теперь можно считать, что первый шаг сделан. Для получения окончательного решения надо просто продолжить наши рассуждения. Поскольку прогноз участ- ника А оказался неверным, значит, участник В также не стал победителем. Остается единственный возможный вариант, в котором победителем стал участник С. Итак, участник С выиграл соревнования, и его прогноз оказался верным. Отсюда можно сделать вывод, что участник А занял третье место. Это означает, что участники финишировали либо в порядке CBAD, либо в порядке CDAB. Но первый вариант нужно отбросить, так как прогноз участника В не оправдался. Следова- тельно, участники финишировали в порядке CDAB.

Конечно, сказать, что нужно сделать первый шаг и занять оптимальную позицию, – совсем не то же самое, что сказать, как это сделать. Первоначальный прорыв, а затем осознание того, как закрепить полученный успех, чтобы суметь найти окончательное решение задачи, потребуют значительных усилий от того, кто ее решает. Однако существует несколько об- щих подходов, предложенных математиком Полиа и другими исследователями, подсказывающими, как можно осуществить этот первоначальный прорыв. Один из подходов состоит в том, чтобы работать с задачей в обратном порядке. Например, если задача заключается в том, чтобы найти способ получения определенного конечного результата из заданного начально- го, можно начать поиск с конечного результата и попытаться пройти путь к заданному начальному. Этот подход будет поле- зен, если потребуется найти алгоритм складывания бумажной птички, упомянутый в предыдущем разделе. Логично начать с попытки развернуть сложенную птичку с целью понять, как она была сделана.

Другой общий подход к решению задачи состоит в поиске связанных с ней проблем, которые или легче решаются, или уже были решены раньше. Позже предпринимается попытка применить способ их решения к данной задаче. Этот метод осо- бенно важен в контексте разработки программ. Часто при разработке программы основная трудность заключается в создании общего алгоритма для решения всех разновидностей данной задачи. Другими словами, если нам необходимо разработать программу для упорядочения списка имен в алфавитном порядке, наша задача не сводится к сортировке отдельного списка, а заключается в нахождении алгоритма, пригодного для сортировки любого списка имен. Рассмотрим следующий набор инст- рукций.

Поменять местами имена David и Alice. Поместить имя Carol между именами Alice и David. Поместить имя Bob между именами Alice и Carol.

Этот набор позволяет правильно выполнить сортировку списка, состоящего из имен David, Alice, Carol и Bob, но он не является тем общим алгоритмом, который мы ищем. Нам же нужен алгоритм, который в состоянии выполнить сортировку как данного списка, так и любого другого, который может встретиться. Однако найденное решение сортировки конкретного списка не является совершенно бесполезным для разработки общего алгоритма. Мы можем, например, продвинуться в ре- шении, рассматривая такие частные случаи, как попытки найти oбщий принцип, которые, в свою очередь, послужат основой для создания искомого общего алгоритма. В этом случае искомое решение, в конце концов, будет найдено с помощью мето- да решения набора взаимосвязанных частных задач.

Еще один подход к проблеме "с чего начинать" заключается в применении метода поэтапного уточнения, который предполагает, что задачу не следует пытаться решить сразу же и целиком во всех ее деталях. Согласно этому методу, иссле- дователь должен разбить задачу на ряд подзадач. Идея заключается в том, что при разбиении исходной задачи на подзадачи появляется возможность найти общее решение как последовательность этапов, на каждом из которых решается задача, более простая по сравнению с исходной. Поэтапное уточнение подразумевает также, что каждый из этапов, в свою очередь, можно разбить на меньшие, а те – на еще меньшие, так что, в конце концов, вся задача сводится к набору легко разрешимых подза- дач.

Поэтапное уточнение является нисходящим методом, так как его развитие происходит в направлении от общего к част- ному. В противоположность этому, восходящие методы предусматривают развитие от частного к общему. Хотя в теории эти подходы противоположны, на практике они просто дополняют друг друга. Например, разбиение задачи, предлагаемое нис- ходящим методом поэтапного уточнения, обычно осуществляется интуитивно с использованием восходящей модели.

Решениям, полученным с помощью метода поэтапного уточнения, свойственна естественная модульная структура. Именно в этом кроется основная причина популярности этого метода при разработке алгоритмов. Если алгоритм имеет есте- ственную модульную структуру, то он легко реализуется в модульном представлении, способствующем созданию удобных в сопровождении программ. Более того, модульная структура, создаваемая в процессе поэтапного уточнения, легко совмеща- ется с концепцией коллективного программирования, в соответствии с которой несколько человек объединяются в команду, имеющую своей задачей разработку определенного программного продукта. После того как исходная задача будет разбита на подзадачи (потенциальные модули), члены команды смогут работать над ними независимо, не мешая друг другу.

Метод поэтапного уточнения пользуется широкой популярностью при разработке программного обеспечения. Однако, несмотря на все его преимущества, этот метод отнюдь не является последним словом науки в отношении создания алгорит- мов. В сущности, он представляет собой только средство организации работы, и все его возможности по решению задач яв- ляются лишь следствием этой организации. Вполне естественно использовать метод поэтапного уточнения при организации общенациональной политической кампании, написании курсовой работы или заключении торгового соглашения. Аналогич- ным образом для большинства проектов разработки программного обеспечения из области обработки данных характерна большая роль организационного компонента. Задача этих проектов состоит не столько в создании нового сенсационного ал- горитма, сколько в представлении решаемых задач таким образом, чтобы их можно было реализовать в виде согласованно функционирующего пакета программ. Поэтому метод поэтапного уточнения по праву стал основой всей методологии проек- тирования в области обработки данных.

Однако поэтапное уточнение остается всего лишь одной из многих методологий проектирования, представляющих интерес для специалистов в области компьютерных наук. Поэтому не следует впадать в заблуждение, полагая, что все алгоритмы могут быть созданы с помощью этого метода. Фактически применение при решении задач предвзятых представлений и заранее выбран-

ных схем в некоторых случаях может даже усложнить изначально простое задание. Рассмотрим следующую задачу.

Когда вы садились в лодку, ваша шляпа упала в воду, но вы этого не заметили. Скорость течения реки 2,5 мили в час, и ваша шляпа поплыла вниз по течению. Тем временем вы поплыли в лодке вверх против течения со скоростью 4,75 мили в час (относительно воды). Спустя 10 минут вы заметили пропажу шляпы, развернули лодку и поплыли вниз по реке догонять вашу шляпу. Через какое время вы поймаете свою шляпу?

Большинство студентов, изучающих алгебру в высшей школе, а также любителей карманных калькуляторов начнут решение этой задачи с определения, какое расстояние прошла лодка за 10 минут вверх по течению, и какое расстояние за это время проплыла шляпа вниз по течению. Затем они попытаются вычислить, сколько времени понадобится лодке, чтобы пройти вниз по течению до той точки, где находится шляпа. Но ведь пока лодка будет идти к этой точке, шляпа будет уплы- вать дальше вниз по течению! Таким образом, они, весьма вероятно, попадут в цикл вычислений, где будет находиться шля- па в тот момент, когда лодка достигнет того места, где шляпа была на предыдущем этапе расчета.

На самом же деле задача гораздо проще. Весь фокус состоит в том, чтобы суметь противостоять стремлению писать формулы и делать вычисления. Необходимо просто отложить эти навыки в сторону и взглянуть на задачу в ее истинном све- те. Суть всей проблемы в реке. В данном случае тот факт, что вода движется относительно берегов, не имеет никакого зна- чения. Представьте себе ту же задачу на длинной конвейерной ленте. Сначала решим поставленную задачу, когда лента не- подвижна. Если вы, стоя на ленте, положите шляпу у своих ног, а затем будете идти вдоль ленты в течение 10 мин, то вер- нуться к шляпе вы сможете за те же 10 мин. Теперь включим конвейер. Это будет означать, что сначала вы пойдете против движения ленты. Но поскольку вы, как и шляпа, находитесь на ленте, это не изменит ваших взаимоотношений с лентой и шляпой. Вам по-прежнему потребуется 10 мин, чтобы вернуться к оставленной шляпе.

В результате можно прийти к заключению, что создание алгоритмов является сложным искусством, которое необходи- мо постоянно совершенствовать, а не изучать как предмет, состоящий из хорошо определенных методологий. Учить решать задачи, следуя четко определенным методологиям, значит "загубить" творческие способности учащихся, которые, напротив, нужно всемерно развивать.

Вопросы для самопроверки

1.     Найдите алгоритм решения следующей задачи и ответьте на дополнительные вопросы.

а) Для заданного положительного числа n найдите такую комбинацию целых положительных чисел, произведение ко- торых максимально среди всех возможных комбинаций целых положительных чисел, сумма которых равна n. Например, если n равно 4, то искомый список есть (2, 2), так как 2*2 больше, чем 1*1*1*1, 2*1*1 и 3*1. Для n, равного 5, искомая ком- бинация будет (2, 3).

б) Какова искомая комбинация для n = 2001?

в) Объясните, как вам удалось продвинуться в решении этой задачи.

2.     Найдите алгоритм решения следующей задачи и ответьте на дополнительные вопросы.

а) Пусть дана квадратная шахматная доска размером

2n ´ 2n , где n – целое положительное число, и коробка с L-

образными фишками, каждая из которых может закрыть в точности три квадрата на доске. Если вырезать из доски один ка- кой-либо квадрат, сможем ли мы покрыть оставшуюся часть доски фишками таким образом, чтобы они не перекрывались и не выступали за край доски?

б) Объясните, как предложенное решение этой задачи может быть использовано, чтобы показать, что 2ⁿ -1 делится на

3 для любых целых положительных n.

в) Как ответы на два предыдущих вопроса связаны с фазами решения задач, предложенными математиком Полиа?

3.     Декодируйте следующее сообщение и объясните, как вам удалось сделать первый шаг в поисках решения:

Pdeo eo pda yknnayp wjosan.