МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ  РЕСПУБЛИКА УЗБЕКИСТАН 

 

ФЕРГАНСКИЙ ФИЛИАЛ ТАШКЕНТСКОЙ МЕДИЦИНСКОЙ АКАДЕМИИ

 

КАФЕДРА «БИОФИЗИКИ, БИОХИМИИ И ИНФОРМАЦИОННЫХ

ТЕХНОЛОГИИ»

 

«Создание моделей в программе Mathcad»

 

 

 

 

(учебное методическое пособие)

 

 

 

                        

 

 

Фергана 2020

                                                                                                                                                           2

 

Это методическое пособие предназначено для студентов в области лечебное дело, медико-профилактическое дело, биомедицинское инженерия по предмету информационные технологии в медицине для моделирования медицинских задач и их решение в области информационных технологий в медицине.

 

Составитель:

 

Абдуманонов А.А.      Рецензент:	- старший преподаватель кафедры «Биофизики, биохимии и информационных технологий» Ферганского филиала ТМА
Халилов Д.А.	- Профессор Ферганского филиала Ташкентского университета информационных технологий имени Мухаммеда Аль Хорезми.
Карабаев М.К.	- Профессор кафедры «Биофизики, биохимии и информационные технологии» Ферганского филиала ТМА.

Данное пособие обсуждалось на заседании кафедры «Биофизики, биохимии и информационных технологий» и рекомендовано к рассмотрению не УМС Ферганского филиала ТМА. 

Протокол №______ “____” ________ 2020 г.

 

Данное пособие было рассмотрено и одобрено Советом Ферганского филиала TМA. 

Протокол №_______ “____” _______ 2020 г.

Содержание

Введение................................................................................................................... 6

Модель Ло́тки — Вольтерра́ (Хищник-Жертва)....................................................... 7

Алгоритм выполнения работы:........................................................................... 8

Варианты заданий:............................................................................................ 14

Модель спроса-предложения.................................................................................. 15

Содержательная постановка задачи.................................................................. 15

Концептуальная постановка............................................................................. 15

Математическая постановка............................................................................. 16

Решение задачи................................................................................................. 16

Решения задачи на MathCAD:.......................................................................... 17

Варианты заданий:............................................................................................ 18

Модель динамики численности популяции............................................................ 19

Содержательная постановка задачи.................................................................. 20

Концептуальная постановка задачи.................................................................. 20

Математическая постановка задачи для модели Мальтуса.............................. 20

Решение задачи................................................................................................. 21

Математическая постановка задачи для модели Ферхюльста.......................... 21

Решение задачи................................................................................................. 22

Реализации задачи на MathCAD:...................................................................... 22

Варианты заданий:............................................................................................ 24

Метод Эйлера......................................................................................................... 24

Реализация метода на MathCAD:...................................................................... 25

Варианты заданий:............................................................................................ 26

Нелинейный осциллятор Ван дер Поля.................................................................. 27

Реализация уравнения на MathCAD:................................................................ 29

Вычислительный блок Given/Odesolve............................................................. 30

Варианты заданий:............................................................................................ 31

Аттрактор Лоренца................................................................................................. 31

Реализация аттрактора на MathCAD:................................................................ 32

Варианты заданий:............................................................................................ 36

Список использованной литературы:..................................................................... 37

 

Введение

 

В данной работе рассмотрены реализации математических методов и моделей в пакете MathCAD. В конце каждой главы даётся по 20 однотипных заданий для самостоятельного решения. Характерной особенностью пакета MathCAD является использование привычных стандартных математических обозначений, то есть документ на экране выглядит точно так же обычный математический расчет. Для использования пакета не требуется изучать какую-либо систему команд, как, например, в случае пакетов Mathematica или Maple. Пакет ориентирован в первую очередь на проведение численных расчетов, но имеет встроенный символический процессор Maple, что позволяет выполнять аналитические преобразования. В последних версиях предусмотрена возможность создавать связки документов Mathcad с документами Mathlab. В отличие от упомянутых выше пакетов, Mathcad является средой визуального программирования, то есть не требует знания специфического набора команд.

Для начала вычислений в среде MathCAD необходимо познакомится с элементами управления. Как и в аналогичных windows приложениях, имеется возможность сохранить результат вычислений, либо открыть предыдущий проект, в разделе Файл (File), выбрав соответствующие команды. Интерфейс приложения крайне прост в освоении. Но для более удобной работы в MathCAD необходимо настроить панель инструментов, выбрав оттуда все необходимые для работы панели, и расположив их на экране наиболее удобным образом (в последствии программа запомнит расположение этих элементов, и при старте они будут появляться там, где вы их определите). Для этого откроем вкладку Вид-> Панель инструментов и установим флажки напротив необходимых компонентов:

 

 

 

Далее в процессе работы мы познакомимся с ними подробнее. 

 

Модель Ло́тки — Вольтерра́ (Хищник-Жертва)

 

Модель Лотки — Вольтерра (более правильным является произношение Вольте́рры, однако этот вариант мало распространён в русском языке) — модель межвидовой конкуренции, названная в честь её авторов — (Лотка, 1925; Вольтерра 1926), которые предложили модельные уравнения независимо друг от друга.

 

Такие уравнения можно использовать для моделирования систем «хищник-жертва», «паразит-хозяин», конкуренции и других видов взаимодействия между двумя видами (Одум, 1986)

 

В математической форме предложенная система имеет следующий вид:

 

 

 

 

 

 

 

где: - количество жертв,

-  количество хищников,

-  время,

  , , ,  - коэффициенты, отражающие взаимодействия между видами.

 

Два дифференциальных уравнения моделируют временную динамику численности двух биологических популяций жертвы Y0 и хищника Y1. Предполагается, что жертвы размножаются с постоянной скоростью C, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом r), и умирают естественным образом (смертность определяется константой D). Рассчитаем три решения D, G, P для разных начальных условий.

Алгоритм выполнения работы:

 

1.     Создаём новый файл MathCAD’ a: - меню Файл->Создать-

> в появившимся окне выбираем первый параметр - Чистый рабочий лист, и нажимаем кнопку ОК.

2.     Наводим курсор на то место, где собираемся объявить начальные значения параметров:

 

3.     Нажимаем клавишу C, затем вводим двоеточие : и знак равно = , на экране появится следующее:

 

Это значит что MathCAD ожидает ввода значения переменной С, вводим значение 0.1, выводим курсор с области рамки, и нажимаем левую кнопку мыши. Значение задано.

 

Примечание: Иногда пользовательские переменные предопределяют встроенные константы в MathCAD (появляется зеленая волнистая линия подчеркивания), на результате вычислений это не сказывается, но если вы собирались использовать их в программе, вам следует задать другое имя переменной.

 

4.     Аналогичным образом задаём значения параметрам D и r:

 

 

5.     Далее задаём функцию F c аргументами t и y: нажимаем клавишу F, открываем круглые скобки клавишей (, нажимаем клавишу t, затем ставим запятую , и вводим аргумент y нажатием соответствующей клавиши, закрываем скобку кнопкой ), ставим двоеточие : 

 

 

5.                 Открываем вкладку Вид->Панель инструментов>Матрицы появится окошко с соответствующими методами для работы:

 

 

 

6.                 Нажимаем на кнопку «Матрица или вектор»:

 

 

 

7.                 В появившимся окне задаём количество строк равным двум, и один столбец, нажимаем клавишу ОК.

 

 

 

8.                 В появившихся скобках записываем первое уравнение: 

 

 

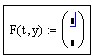
9.                 Нажимаем клавишу С, затем умножить * вводим y с индексом ноль, для этого после того как вы ввели y, нажмите на иконку «Нижний индекс» в окошке «Матрица»:

 

и введите 0:

 

 

Нажмите стрелку «вправо», для того чтобы продолжить запись уравнения вне рамках нижнего индекса. Далее введите: - r * y с индексом

0 умноженное на y с индексом 1, проделанным ранее способом.

 

10.            Нажмите левой кнопкой мыши по черному квадрату расположенному чуть нижу первого уравнения:

 

Появится синий курсор, это означает, что вы можете продолжать ввод второго уравнения. 

 

11.            Уже известным вам способом запишите второе уравнение, чтобы функция выглядела следующим образом:

 

 

 

12.            Далее зададим значения параметрам:

  

Примечание: Здесь t0 и t1 не имеют нижних индексов, а просто 1 и 0 просто разные обозначения двух переменных.

 

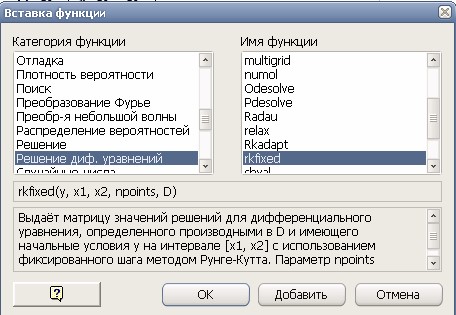
13.            Затем, внутри переменной D вызовем функцию rkfixed, производящую вычисление дифференциального уравнения по методу Ренге-Кутта. Для этого во вкладке Добавить, выберем строку Функцию, в появившемся окне Вставка функций выберем Решение диф. уравнений в разделе Категория функции и rkfixed в разделе Имя функции, нажмём кнопку ОК:

 

 

 

14.            Появится следующая строка:

 

 

Далее в окошке Матрица нажимаем на кнопку Матрица или векторы, задаём количество строк равным двум, а столбцов равным единице:

 

 

15.            Приводим строку к следующему виду: 

 

 

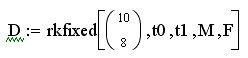
16.            Аналогичным образом создаём переменные G и P со следующими значениями:

 

 

17.            Для того чтобы MathCAD численно решил дифференциальные уравнения с параметрами из переменной D, необходимо ввести имя переменной D и знак равно, и щелкнуть кнопкой мыши на пустой рабочей области. Решение будет выглядеть так:

 

 

  

18.            Далее нам нужно построить график функции. Для этого, во вкладке Вид выберем Панели инструментов > Графики. В появившемся окошке нажмём на кнопку Х-У график:

 

 

Появится следующая заготовка: 

 

 

19.            По оси х, введём переменную D, затем нажмём в окошке Матрица кнопку столбец матрицы:

 

 

 

В появившиеся сверху скобки внесём значение единица 1:

 

 

20.            Далее поставим синий курсор справа перед D, нажмём пробел и введём следующие значения, аналогичным образом заполним пустующие поля по оси y, график должен иметь вид:

 

 

 

Нажав левой кнопкой мыши на пустую рабочую область, и немного подождав, получим следующий фазовый портрет (справа) системы "хищник—жертва":

 

 

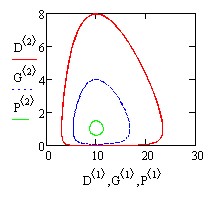
21.            Для получения графика решения, проделаем описанные выше операции, но уже с другими параметрами, по оси х, введём D c нулевым столбцом матрицы, а по оси у – D с первым и вторым столбцами матрицы. Получим следующий график:

 

 

Модель замечательна тем, что в такой системе наблюдаются циклическое увеличение и уменьшение численности и хищника, и жертвы, так часто наблюдаемое в природе. Фазовый портрет системы представляет собой концентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численности обеих популяций существенно зависят от начальных условий — после каждого периода колебаний система возвращается в ту же точку. Динамические системы с таким поведением называют негрубыми.

Варианты заданий:

 

Произвести вычисление модели Хищник-Жертва на MathCAD’е в соответствие с вышеуказанным способом, используя нижеследующие параметры получить график решения и фазовый портрет модели:

 

1.                 С=0.4, D=1, r=0.1, M =650, t0=1, t1=990

2.                 С=0.3, D=1.1, r=0.1, M =750, t0=1, t1=160

3.                 С=0.2, D=1.2, r=0.1, M =850, t0=1, t1=1000

4.                 С=0.1, D=1.3, r=0.1, M =950, t0=1, t1=2000

5.                 С=0.15, D=1.4, r=0.1, M =8550, t0=1, t1=3000

6.                 С=0.5, D=0.9, r=0.1, M =1650, t0=1, t1=600

7.                 С=0.6, D=0.8r=0.1, M =1340, t0=1, t1=700

8.                 С=0.7, D=0.7=0.1, M =530, t0=1, t1=800

9.                 С=0.8, D=0.6=0.1, M =950, t0=1, t1=650 10.       С=0.9, D=0.5=0.1, M =550, t0=1, t1=500

11.            С=0.65, D=0.4=0.1, M =250, t0=1, t1=100

12.            С=0.32, D=0.3=0.1, M =340, t0=1, t1=108

13.            С=0.21, D=059=0.1, M =370, t0=1, t1=170

14.            С=0.45, D=1/4 r=0.1, M =3850, t0=1, t1=100

15.            С=0.41, D=1/5, r=0.1, M =750, t0=1, t1=10

16.            С=0.2, D=1/6, r=0.1, M =150, t0=2, t1=98

17.            С=0.71, D=1.12, r=0.1, M =250, t0=1, t1=10

18.            С=0.52, D=1.23, r=0.1, M =200, t0=1.2, t1=100

19.            С=0.43, D=1.42, r=0.2, M =650, t0=1.1, t1=10

20.            С=0.34, D=1.32, r=0.3, M =450, t0=1.1, t1=100

Модель спроса-предложения

Содержательная постановка задачи

 

Представим себя на месте некоего фермера, который каждый год выращивает на своем поле пшеницу на продажу. Запасов, которые хранились бы больше года, он не делает. То есть живет если и не одним днем, то одним годом. 

Решение о том, сколько пшеницы сеять, принимается простейшим образом, с учетом цен предыдущего года, а именно: если цены были высокие – в этом году надо сеять пшеницы больше, а если низкие – меньше. Спрос на пшеницу в течение года зависит прежде всего от ее цены в момент продажи. Когда цена растет, спрос, естественно, падает. И наоборот. Необходимо описать поведение цен в ближайшие годы как функцию от первоначальной цены.

Концептуальная постановка

 

Введем обозначения:

 

•        pn – цена за единицу веса пшеницы в n-м году

•        sn – предложение (объем выращенной фермером пшеницы)

пшеницы в n-й год (в единицах веса); 

•        dn – спрос на пшеницу в n-й год (в единицах веса). Примем следующие предпосылки.

•        Объектом исследования является зависимость цены pn на пшеницу от ее первоначальной цены p0. 

 

•        Предположим, что предложение sn+1 будущего года зависит линейно от цены pn в этом году: чем выше pn, тем больше sn+1 . Очевидно, что цена на пшеницу не должна быть меньше некоторой минимальной величины, покрывающей затраты на ее производство, лишь в этом случае величина предложения sn+1 будет больше нуля. 

•        Предположим, что спрос будущего года dn+1 зависит линейно от цены  pn+1 в том же году: чем выше цена pn+1, тем меньше спрос dn+1.

Очевидно, что самый большой спрос на пшеницу должен существовать     при pn+1=0. 

•        Предположим,  что  рыночная  цена pn+1определяется  равновесием между спросом dn+1и предложением sn+1. Требуется описать поведение цен в последующие годы p1, p2, p3, ... в зависимости от значения цены p0.

 

Математическая постановка

 

Выпишем систему уравнений, исходя из принятых предположений: sn+1 = а pn - b (1) dn+1 = - c pn +1 + g (2)

sn+1 = dn+1 (3)

 

Здесь a, b, c, g - положительные вещественные числа. Значения этих величин характеризуют динамику цены на рынке и специфичны для каждого продукта, например, отношение b/a характеризует минимально допустимую цену, а  величина g - максимально возможный спрос; p0 задано.

 

 

Решение задачи

 

Подставляя (1) и (2) в (3), получим:

а pn - b = - c pn+1 + g.

 

Введем новые положительные константы:

A = a/c>0, B = (b/c + g/c) > 0

 

Приходим к соотношению:

pn+1 = B - A pn

 

Это уравнение представляет некоторое линейное рекуррентное соотношение, которое позволяет построить последовательность интересующих нас решений p1, p2, p3, ... .

Попробуем вывести общую формулу pn = f(p0). Пусть p0 задано. 

 

Тогда, p1=B-Ap0 p2=B(1-A)+A^2 p0

p3=B(1-A+A^2)-A^3 p0

 

Некоторая зависимость проглядывается, но вряд ли она очевидна. Но стоит умножить и разделить первое слагаемое на (1+А) – и все встает на свои места. Теперь общая формула очевидна:

pn=(B/1+A)(1-(-A)^n)+(-A)^n p0

 

Проведем расчеты для некоторых значений A и B. Предварительное изучение уравнения показывает, что основное влияние на динамику цены оказывает параметр А. Какое именно – выясним, положив В=1.

 

 

 

Вычислим для различных значений А изменение цены из года в год в течение 12 лет:

 

 

Решения задачи на MathCAD:

 

 

 

Далее уже известным вам из предыдущей лабораторной работы, способом, построим график решения задачи: 

 

 

 

Из полученного графика видно, что не смотря на различные начальные условия цен на пшеницу х0, х1, х2, по прошествии нескольких лет цена на неё приходит к оптимальному значению в ~0.66 у.е. когда спрос равен предложению.

 

Варианты заданий:

 

Произвести вычисление на MathCAD’е в соответствии вышеуказанному решению модели спроса-предложения, узнать оптимальную цену на пшеницу за определенное время, изменяя параметры:

 

1.       A=0.55, B=1, n=15, x0=1, x1=3, x2=5

2.       A=0.6, B=1, n=21, x0=6, x1=3, x2=1

3.       A=0.7, B=1.1, n=43, x0=1, x1=3, x2=5

4.       A=0.8, B=1, n=50, x0=1, x1=3, x2=5

5.       A=0.9, B=1, n=71, x0=4, x1=7, x2=3

6.       A=0.5, B=0.9, n=10, x0=3, x1=1, x2=5

7.       A=0.57, B=1, n=14, x0=2.5, x1=5, x2=6

8.       A=0.45, B=1, n=9, x0=7, x1=3, x2=5

9.       A=0.35, B=1, n=11, x0=8, x1=3, x2=5

10.   A=0.45, B=1, n=11, x0=7, x1=3, x2=5

11.   A=0.85, B=1, n=61, x0=5, x1=3, x2=2

12.   A=0.59, B=1.2, n=24, x0=1, x1=5, x2=9

13.   A=0.53, B=1, n=11, x0=5, x1=3, x2=4

14.   A=0.32, B=1, n=11, x0=1, x1=3, x2=4

15.   A=0.38, B=1, n=11, x0=1, x1=2, x2=5

16.   A=0.2, B=1, n=5, x0=6, x1=3, x2=5

17.   A=0.7, B=1, n=80, x0=4, x1=3, x2=2

18.   A=0.57, B=1.1, n=19, x0=3, x1=6, x2=2

19.   A=0.6, B=1, n=20, x0=1, x1=3, x2=5

20.   A=0.42, B=0.9, n=13, x0=3, x1=5, x2=1

Модель динамики численности популяции

 

Одним из важнейших разделов современной биологии и экологии является биология популяций. Популяцией в биологии называют сообщество особей одного вида, занимающих некоторую область пространства на нашей планете. Вопросы, которые приходится решать биологии популяций, разнообразны. Например, что получится, если поместить тысячу карасей в пруд с ограниченными пищевыми ресурсами? Что изменится, если выпустить туда еще пятьдесят щук, поедающих в среднем по два карася в день? Какая судьба постигнет вирус, вызывающий гибель определенного вида животных и распространяющийся с известной скоростью, зависящей от плотности популяции? Какими темпами будет увеличиваться численность людей на Земле? Список подобных вопросов можно продолжать и продолжать.

 

Характерной особенностью биологии как науки является то, что одним из основных методов исследования данной дисциплины все еще остается наблюдение. Объяснить это можно множеством причин, одной из которых является сложность формализации параметров, описывающих различные виды живых существ. В то же время отличительной чертой биологии популяций является то, что для исследования динамики популяций достаточно интенсивно используется математическое моделирование.

 

В природе встречаются популяции организмов как с дискретным, так и с непрерывным периодом размножения. К первым можно отнести многие виды насекомых (бабочки, майские жуки, саранча), рыб, птиц и млекопитающих с привязкой периода размножения к определенным временам года. Ко вторым относятся живые организмы, процесс размножения которых не привязан ко временам года (в первую очередь это домашние животные и человек). Модели для динамики популяций с дискретным и непрерывным периодом размножения существенно отличаются. В частности, для популяций с непрерывным периодом размножения применим аппарат дифференциального исчисления. Далее будут рассматриваться только популяции с непрерывным периодом размножения.

 

Первая модель динамики популяций была предложена священником Томасом Мальтусом еще в 1778 г. в опубликованной им работе “Трактат о народонаселении”. Хотя модель, предложенная Мальтусом, касалась народонаселения Земли, ее можно распространить на любую популяцию живых организмов. Рассмотрим эту модель более подробно.

 

Содержательная постановка задачи

 

Как будет изменяться численность популяции, если сдерживающие факторы (болезни, хищники, конкурирующие виды, ограниченность питания и т.п.) отсутствуют?

Концептуальная постановка задачи

 

Исследование популяции провести при следующих допущениях:

(1) объектом исследования является некоторая популяция организмов;

(2) сдерживающие факторы роста популяции отсутствуют;

(3) скорость прироста численности популяции прямо пропорциональна величине численности популяции.

Последние два предположения являются относительно грубыми. Их применение оправдано на довольно коротком начальном этапе развития популяции (например, при начальном развитии колонии бактерий в автоклаве при достаточно интенсивном перемешивании биомассы).

 

Математическая постановка задачи для модели Мальтуса

 

Пусть x(t) – численность популяции в момент времени t. Функцией прироста R(t) называют относительное изменение численности за время

∆t:

 

 

 

Если эта величина – некоторая константа r, то закон, управляющий динамикой численности популяции в модели Мальтуса, имеет вид:

 

 

 

Переходя к пределу при ∆t → 0, получим следующее обыкновенное дифференциаль-ное уравнение (1):

  

Итак, для решения поставленной задачи необходимо найти решение уравнения (1) при начальном условии (2):

 

 

Решение задачи

 

Для решения уравнения (1) можно воспользоваться методом разделения переменных:

 

 

 

Окончательно имеем (1):

 

 

 

Полученное по модели Мальтуса решение (1) предсказывает неограниченный рост численности популяции по экспоненциальному закону. В действительности неограниченный рост невозможен, так как сдерживающие факторы присутствуют всегда. Численность популяции, как правило, испытывает небольшие колебания относительно некоторой величины.

Одним из первых обратил на это внимание П.Ф. Ферхюльст, сформулировав в 1845 г. закон, содержащий ограничение на рост популяции. Он объяснил это тем, что любая экологическая ниша можетобеспечить существование популяции только определенного максимального размера xmax и что коэффициент прироста должен сни- жаться, когда размеры популяции приближаются к xmax. Будем

измерять численность популяции в относительных единицах:

 

 

 

Тогда функцию прироста по Ферхюльсту можно записать следующим образом (2):

 

 

 

 

С учетом (1) запишем математическую постановку задачи для модели Ферхюльста.

 

 

Математическая постановка задачи для модели Ферхюльста

 

 

Найти решение задачи Коши (3):

 

 

при начальных условиях:

 

 

 

Решение задачи

 

Уравнение (3) можно проинтегрировать методом разделения переменных:

 

 

в результате чего получим решение:

 

 

 

Реализации задачи на MathCAD:

 

 

 

Примечание: Для установки переменного значения t, следует открыть вкладку Вид, Панель управления, Матрица и нажать на кнопку «Область переменной»:

 

 

 

Параметр e, в функции X(t, N) – экспонента, для её вставки необходимо открыть вкладку Вид, Панель инструментов, Калькулятор, и нажать кнопку «Экспонента»:

 

 

 

Далее создаём график, следующего вида:

 

 

 

На созданном нами выше, графике, показано изменение относительной численности популяции во времени при различных начальных значениях N0 и r (условие N0 > 1 возможно, если в период времени до начала рассмотрения изменения популяции окружающие условия были более благоприятны для нее). 

 

Варианты заданий:

 

Произвести вычисление на MathCAD’е, в соответствии с вышеуказанной моделью изменяя начальные параметры:

 

1.       t=0..5, r=2, x0=2, x1=0.6

2.       t=0..10, r=2.1, x0=2.5, x1=0.5

3.       t=0..7, r=2.5, x0=1.9, x1=0.4

4.       t=0..11, r=2.3, x0=1.5, x1=0.7

5.       t=0..15, r=1.9, x0=2.1, x1=0.8

6.       t=0..20, r=2.2, x0=2.6, x1=0.6

7.       t=0..5, r=3, x0=3, x1=0.4

8.       t=0..9, r=2, x0=2, x1=0.1

9.       t=0..15, r=2.5, x0=3, x1=0.2

10.   t=0..10, r=2, x0=2, x1=0.8

11.   t=0..6, r=2.1, x0=2, x1=0.3

12.   t=0..9, r=2.4, x0=2.2, x1=0.6

13.   t=0..20, r=2.2, x0=1.9, x1=0.5

14.   t=0..5, r=2.3, x0=2.05, x1=0.7

15.   t=0..10, r=2.1, x0=2, x1=0.1

16.   t=0..50, r=2.5, x0=3, x1=0.9

17.   t=0..3, r=2.3, x0=2.3, x1=0.3

18.   t=0..6, r=1.5, x0=2, x1=0.2

19.   t=0..4, r=2.5, x0=2, x1=0.3

20.   t=0..5, r=2.2, x0=2.2, x1=0.2

 

 

Метод Эйлера

 

Решим задачу Коши для дифференциального уравнения первого порядка y’= f(x,y) методом Эйлера. 

 

Пусть правая часть уравнения равна f(x,y)=x*y 

 

1.   Зададим границы изменения x: x_min=0,  x_max=1 

2.   Зададим число точек и величину шага: n=10, h=(x_max-x_min)/n

3.   Зададим начальные условия: y0= 1 x0 = x_min 

4.   Вычислим x и y по формулам Эйлера j=1..n 

 

                                                 

 

Представим результат графически и сравним его с аналитическим решением y1(x)=exp(x^2/2), при z=0..1 с шагом 0.1, k=0..n

 

Реализация метода на MathCAD:

 

 

 

 

 

 

 

Точное аналитическое решение и решение, полученное численно, отличаются в точке x=1 на y1(1) – yn =0.062

То есть относительная ошибка составляет 0.062%, с увеличением количества шагов n, она снижается, так при n = 50, относительная ошибка

(погрешность) будет равна 0.013%.

 

Варианты заданий:

 

Произвести вычисление на MathCAD’е в соответствие с вышеуказанным решением по методу Эйлера, узнать относительную погрешность, изменяя параметры:

 

1.                 x_min=0.1, x_max=1, n=20, y0 =0.9

2.                 x_min=0, x_max=0.99, n=18, y0 =1

3.                 x_min=0.2, x_max=1, n=29, y0 =1.9

4.                 x_min=0, x_max=1.1, n=40, y0 =1

5.                 x_min=0.3, x_max=1.2, n=50, y0 =1/3

6.                 x_min=0.4, x_max=1, n=60, y0 =1/9

7.                 x_min=0.2, x_max=1, n=70, y0 =1/2

8.                 x_min=0.1, x_max=1, n=30, y0 =1/6

9.                 x_min=0, x_max=0.9, n=90, y0 =1/2

10.            x_min=0.01, x_max=1, n=39, y0 =3/4

11.            x_min=0.02, x_max=1, n=74, y0 =1/8

12.            x_min=0.03, x_max=1, n=11, y0 =0.43

13.            x_min=0.04, x_max=1, n=9, y0 =0.98

14.            x_min=0.05, x_max=0.8, n=65, y0 =0.5

15.            x_min=0.09, x_max=0.09, n=19, y0 =0.3

16.            x_min=0.08, x_max=0.9, n=99, y0 =0.8

17.            x_min=0.07, x_max=0.99, n=19, y0 =0.6

18.            x_min=0.45, x_max=0.69, n=10, y0 =0.53

19.            x_min=0.19, x_max=0.29, n=47, y0 =0.12

20.            x_min=0.69, x_max=0.19, n=9, y0 =0.2

 

 

Нелинейный осциллятор Ван дер Поля

 

 

 

Уравнение Ван дер Поля описывает свободные автоколебания одной из простейших нелинейных колебательных систем (осциллятора Ван дер Поля). В частности, уравнение служит математической моделью (при ряде упрощающих предположений) лампового генератора на триоде в случае кубической характеристики лампы. Характер решений уравнения был впервые подробно изучен Ван дер Полем. 

 

При μ< 1 в системе возникают квазигармонические автоколебания:

 

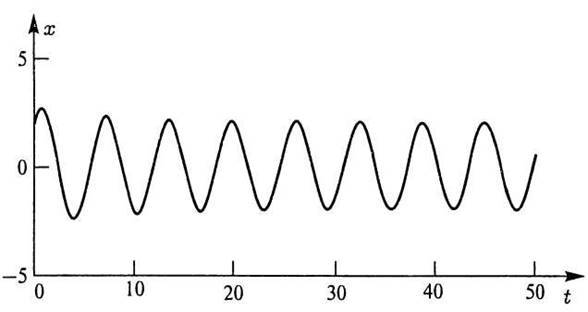 при μ ~1 — сильно несинусоидальные колебания:

 

 

 

 

при μ > 1 — релаксационные колебания: 

 

 

 

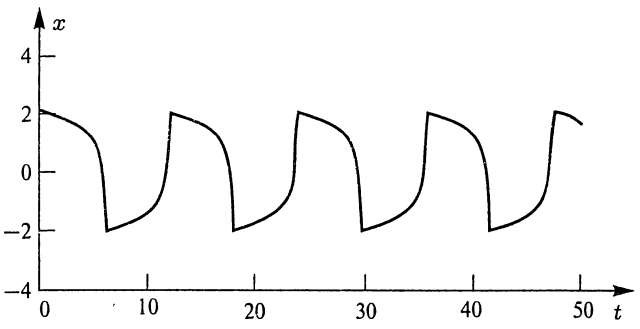
                Независимо    от     начальных    условий     все    фазовые    траектории

стягиваются к предельному  циклу — замкнутой траектории , соответствующей стационарному режиму. В нашем случае автоколебания устанавливаются в системе при любых начальных условиях, в том  числе и при нулевых начальных значениях тока и напряжения. Такой

режим возбуждения  автоколебаний называется мягким. Классическая модель нелинейной

системы, демонстрирующая периодические автоколебания. 

 

При различных начальных условиях фазовая траектория стремится к аттрактору - предельному циклу. 

 

Установившиеся движения представляют собой периодические колебания, математическим образом в фазовом пространстве которых и является предельный цикл.

 

Фазовая траектория автоколебаний:

 

 

Пример фазового портрета автоколебательной системы

 

Реализация уравнения на MathCAD:

 

 

 

Примечание: Для того чтобы вставить греческую букву Мю μ, необходимо открыть вкладку Вид, Панель инструментов, Греческая, и нажать на соответствующую кнопку:

 

 

Примечание: Для того чтобы вставить штрих после у нажмите CTRL+F7 

Вычислительный блок Given/Odesolve 

 

Вычислительный блок для решения одного обыкновенного дифференциального уравнения (ОДУ), реализующий численный метод Рунге-Кутты, состоит из трех частей: 

-                     Given — ключевое слово; 

-                     ОДУ и начальное условие, записанное с помощью логических операторов, причем начальное условие должно быть в форме у (t1) = b; 

-                     odesoive(t, t1) — встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1).

Для вызова функции Odesolve нужно открыть вкладку Добавить,

Функцию, в появившимся окне в разделе Категории функций выберите Решение диф. уравнений, а в разделе Имя функции кликните на Odesolve, и нажмите кнопку ОК.  Далее создайте график, и приведите его к следующему виду:

 

 

 

Если компьютер у вас не самый мощный, то расчет изображенного выше, фазового портрета в MathCAD может занять относительно продолжительное время, что связано с численным определением сначала решения у(t), а потом и его производной.

Неизвестная функция времени y(t) имеет смысл электрического тока, а в параметре μ заложены количественные соотношения между составляющими электрической цепи, в том числе и нелинейной компонентой сопротивления.

 

Варианты заданий:

 

Произвести вычисление на MathCAD’е в соответствии с вышеуказанной реализацией решения, получить фазовый портрет, изменяя следующие параметры:

 

 

1.                 y(0) = 0.02, μ = 1.2, y’=0.05

2.                 y(0) = 0.22, μ = 1.4, y’=0.06

3.                 y(0) = 0.32, μ = 1.8, y’=0.07

4.                 y(0) = 0.42, μ = 2.4 , y’=0.08

5.                 y(0) = 0.52, μ = 2.6, y’=0.09

6.                 y(0) = 0.62, μ = 2.8, y’=0.1

7.                 y(0) = 0.72, μ = 2.9, y’=0.15

8.                 y(0) = 0.82, μ = 0.02, y’=0.17

9.                 y(0) = 0.92, μ = 0.2, y’=0.18

10.            y(0) = 1.02, μ = 0.5 , y’=0.2

11.            y(0) = 3.02, μ = 1.2, y’=0.25

12.            y(0) = 2.32, μ = 0.09, y’=0.35

13.            y(0) = 1.32, μ = 2.03, y’=0.45

14.            y(0) = 0.02, μ = 0.05, y’=0.55

15.            y(0) = 0.09, μ = 1.2, y’=0.65

16.            y(0) = 0.12, μ = 1.2, y’=0.75

17.            y(0) = 2.02, μ = 1.2, y’=0.75

18.            y(0) = 3.02, μ = 2.09, y’=0.8

19.            y(0) = 2.52, μ = 0.2, y’=0.95

20.            y(0) = 1.22, μ = 0.04, y’=0.005

 

Аттрактор Лоренца

 

Аттрактор Лоренца (от англ. to attract — притягивать) ― компактное инвариантное множество L трехмерном фазовом пространстве гладкого потока, которое имеет определённую сложную топологическую структуру и является асимптотически устойчивым, оно устойчиво по Ляпунову и все траектории из некоторой окрестности L стремятся к L при t → ∞. 

 

Аттрактор Лоренца был найден в численных экспериментах Лоренца, исследовавшего поведение траекторий нелинейной системы:

 

 

 

 

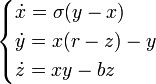
при следующих значениях параметров: σ=10, r=28, b=8/3. Эта система вначале была введена как первое нетривиальное галёркинское приближение для задачи о конвекции морской воды в плоском слое, чем и мотивировался выбор значений σ, r и b, но она возникает также и в других физических вопросах и моделях:

-   конвекция в замкнутой петле;

-   вращение водяного колеса;

-   модель одномодового лазера;

-   диссипативный осциллятор с инерционной нелинейностью.

 

Модель Лоренца является реальным физическим примером динамических систем с хаотическим поведением, в отличие от различных искусственно сконструированных отображений («зуб пилы», «тент», преобразование пекаря, отображение Фейгенбаума и др.).

 

Реализация аттрактора на MathCAD:

          

Поскольку неизвестных функций три, то фазовый портрет системы должен определяться не на плоскости, а в трехмерном пространстве. 

 

 

Примечание: Функция rkfixed можно вызвать открыв вкладку

Добавить, Функцию, и в появившимся окне, в правом списке окна выбрать rkfixed. 

 

 

Примечание: Для того чтобы получить объемный график необходимо открыть вкладку Вид, Панель инструментов, Графики, и нажать кнопку «График плоскости» на панели:

 

 

 

 

 

В появившейся пустой заготовки, напротив синего курсора ввести: (X,Y,Z), и нажать на пустое место в рабочей области. У вас должно получится следующее: 

 

 

 

 

Далее необходимо настроить вид графика. Для этого дважды щелкните левой кнопкой мыши по графику, появится окно Формат 3D графика:

 

 

 

 

 

 

Далее во вкладке График 1, выбираем параметр График разброса:

 

 

 

 

Затем окрываем вкладку Вид, с в разделе Настройка цвета выбираем параметр Карта цветов, и нажимаем кнопку ОК:

 

 

 

 

 

В результате у вас должен получится подобный график: 

 

 

 

 

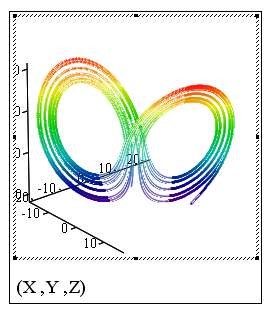
Примечание: Если навести на него курсор и зажать левую кнопку мыши можно разглядывать график с разных сторон, а зажав клавишу Ctrl и крутя колесико мыши, можно увеличивать и уменьшать масштаб графика, для того чтобы лучше его рассмотреть.

 

Решением системы Лоренца при определенном сочетании параметров является странный аттрактор (или аттрактор Лоренца) - притягивающее множество траекторий на фазовом пространстве. В некотором смысле, аттрактор Лоренца является стохастическими автоколебаниями, которые поддерживаются в динамической системе за счет внешнего источника. Решение подобных нелинейных динамических систем можно получить только численно, поэтому их изучение стало бурно развиваться с ростом возможностей вычислительной техники в последние полвека.

Варианты заданий:

 

Произвести вычисление на MathCAD’е в соответствии с вышеуказанной реализацией решения, получить фазовый портрет, изменяя следующие параметры:

 

 

1.                   σ = 10, r = 14, b=2.56, N=1100, y0=(10,10,10)

2.                   σ = 11, r = 15, b=2.4, N=11000, y0=(11,11,11)

3.                   σ = 12, r = 16, b=2.36, N=10000, y0=(9,9,9)

4.                   σ = 13, r = 17, b=2.26, N=9100, y0=(12,12,12)

5.                   σ = 14, r = 18, b=2.1, N=5555, y0=(11,11,11)

6.                   σ = 15, r = 19, b=2.06, N=100000, y0=(10,10,10)

7.                   σ = 9, r = 20, b=2, N=106, y0=(10.5,10.5,10.5)

8.                   σ = 8, r = 21, b=1.96, N=100, y0=(9.3,9.3,9.3)

9.                   σ = 7, r = 22, b=1.85, N=410, y0=(11.2,11,11.1)

10.              σ = 6, r = 23, b=1.7, N=310, y0=(10,10,10)

11.              σ = 5, r = 24, b=1.6, N=510, y0=(9,9,9.1)

12.              σ = 4, r = 25, b=1.55, N=700, y0=(12.5,12,12)

13.              σ = 3, r = 13, b=1.44, N=800, y0=(10.1,10.2,10.3)

14.              σ = 2, r = 12, b=1.26, N=850, y0=(13,13,13)

15.              σ = 10, r = 25, b=1, N=1990, y0=(-10,-10,-10)

16.              σ = 0, r = 10, b=1.9, N=950, y0=(15,15,15)

17.              σ = 1.6, r = 9, b=2.7, N=9100, y0=(10,10,10)

18.              σ = 2.5, r = 8, b=2.8, N=9900, y0=(8,8,8)

19.              σ = 3.14, r = 7, b=3.96, N=7109, y0=(11,11,11)

20.              σ = 6.66, r = 6, b=4.66, N=5100, y0=(14,14,14)

 

Список использованной литературы:

 

1.     Лоренц Э. Детерминированное непериодическое движение // Странные аттракторы. — М., 2009.

2.     Математическое и компьютерное моделирование. Вводный курс: Учебное пособие. Изд. 4-е, испр. — М.: Едиториал УРСС, 2008. — 152 с.

3.     Ю. Ю. Тарасевич Численные методы на Mathcad’е. – Астраханский гос. пед. ун-т: Астрахань, 2010. 

4.     Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 2006

5.     Дьяконов, В. Mathcad 2001: учебный курс; СПб: Питер - Москва, 2001. - 624 c.

6.     Кирьянов Д. Самоучитель Mathcad 11; Книга по Требованию - Москва, 2012. - 544 c.

7.     Любимов Э. В. Mathcad. Теория и практика проведения электротехнических расчетов в среде Mathcad и Multisim; Наука и техника - Москва, 2012. - 400 c.

8.     Макаров Евгений Инженерные расчеты в Mathcad 15. Учебный курс; Питер - Москва, 2011. - 400 c.

9.     Поршнев С. В., Беленкова И. В. Численные методы на базе Mathcad;

БХВ-Петербург - Москва, 2012. - 456 c.

 

            38        39        40