
способ подстановки
Цели: продолжить формирование умения решать системы уравнений способом подстановки; проверить первоначальный уровень усвоения материала.
Ход урока
I. Устная работа.
Является ли пара чисел (–3; 1) решением системы уравнений:
а) 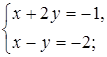 б)
б) 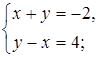 в)
в)
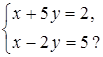
II. Проверочная работа.
Вариант 1
1. Выразите в уравнении х через у и у через х.
а) x + y = ![]() ; б) 2x
– y = 7; в) –3x + 5y
= 1.
; б) 2x
– y = 7; в) –3x + 5y
= 1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 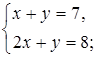 б)
б) 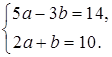
Вариант 2
1. Выразите в уравнении х через у и у через х.
а) x – y = ![]() ; б) x
+ 3y = 5; в) 4x – 5y
= –1.
; б) x
+ 3y = 5; в) 4x – 5y
= –1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 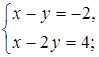 б)
б) 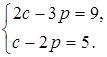
III. Формирование умений и навыков.
На этом уроке учащиеся будут решать системы уравнений, в которых ни один коэффициент при переменных не равен ±1. Сначала нужно разобрать пример 2 из учебника, сделать соответствующие выводы, а затем приступить к выполнению заданий.
1. № 1071.
Следует обратить внимание учащихся, что иногда удобнее выражать переменную вместе с её коэффициентом.
Решение:
а) 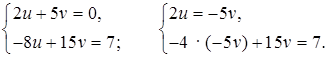
20v + 15v = 7;
35v = 7;
v = ![]() ;
;
2u = –5 ∙ ![]() = –1;
= –1;
u = ![]() .
.
Ответ: 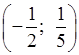 .
.
б) Здесь не получится сделать, как в предыдущей системе, поскольку коэффициенты при переменных не являются кратными.
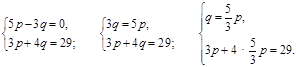
3p + 4 ∙ ![]() p = 29;
p = 29;
3 · 3р + 4 · 5р = 29 · 3;
9р + 20р = 29 · 3;
29р = 29 · 3;
р = 3;
q = ![]() p =
p = ![]() ∙ 3 = 5.
∙ 3 = 5.
Ответ: (3; 5).
в) 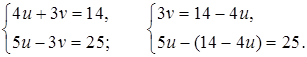
5u – (14 – 4u) = 25;
5u – 14 + 4u = 25;
9u = 39;
u = ![]() .
.
3v = 14 – 4 ∙ 4![]() ;
;
3v = 14 – 17![]() = –3
= –3![]() ;
;
v = –1![]() .
.
Ответ: 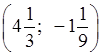 .
.
г) 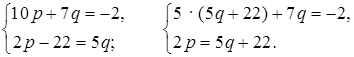
5 ∙ (5p + 22) + 7q = –2;
25p + 110 + 7q = –2;
32q = –112;
q = –3,5.
2p = 5 ∙ (–3,5) + 22;
2р = –17,5 + 22 = 4,5;
р = 2,25.
Ответ: (2,25; –3,5).
2. № 1073.
Решение:
Чтобы найти координаты точки пересечения двух прямых, нужно решить соответствующую систему уравнений.
а) 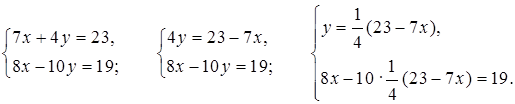
![]()
16х – 5 (23 – 7х) = 38;
16х – 115 + 35х = 38;
51х = 153;
х = 3.
![]()
Ответ: (3; 0,5).
IV. Итоги урока.
– Что называется решением системы уравнений с двумя переменными?
– Сформулируйте алгоритм решения систем уравнений способом подстановки.
– В каких случаях при решении системы уравнений можно выражать переменную вместе с её коэффициентом?
Домашнее задание: № 1072, № 1074.
Вариант 1
1. Выразите в уравнении х через у и у через х.
а) x + y = ![]() ; б) 2x
– y = 7; в) –3x + 5y
= 1.
; б) 2x
– y = 7; в) –3x + 5y
= 1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 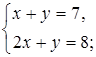 б)
б) 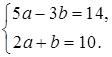
Вариант 2
1. Выразите в уравнении х через у и у через х.
а) x – y = ![]() ; б) x
+ 3y = 5; в) 4x – 5y
= –1.
; б) x
+ 3y = 5; в) 4x – 5y
= –1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 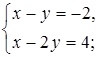 б)
б) 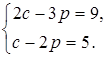
Вариант 1
1. Выразите в уравнении х через у и у через х.
а) x + y = ![]() ; б) 2x
– y = 7; в) –3x + 5y
= 1.
; б) 2x
– y = 7; в) –3x + 5y
= 1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 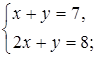 б)
б) 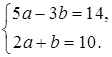
Вариант 2
1. Выразите в уравнении х через у и у через х.
а) x – y = ![]() ; б) x
+ 3y = 5; в) 4x – 5y
= –1.
; б) x
+ 3y = 5; в) 4x – 5y
= –1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 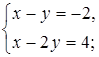 б)
б) 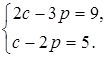
Вариант 1
1. Выразите в уравнении х через у и у через х.
а) x + y = ![]() ; б) 2x
– y = 7; в) –3x + 5y
= 1.
; б) 2x
– y = 7; в) –3x + 5y
= 1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 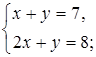 б)
б) 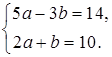
Вариант 2
1. Выразите в уравнении х через у и у через х.
а) x – y = ![]() ; б) x
+ 3y = 5; в) 4x – 5y
= –1.
; б) x
+ 3y = 5; в) 4x – 5y
= –1.
2. Решите систему уравнений способом подстановки и сделайте проверку.
а) 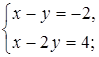 б)
б) 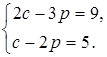
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.