Срезовая работа по математике в 9 классе

Диагностическая работа по математике

9 класс

Вариант 2

Инструкция для учащихся. Работа состоит из 20 заданий. На ее выполнение отводится не более 60 минут. Задания рекомендуется выполнять по порядку, не пропуская ни одного, даже самого легкого. Если задание не удается выполнить сразу, переходите к следующему. Если остается время, вернитесь к пропущенным заданиям.

Часть 1

Указание 1: В заданиях части 1 из предложенных вариантов ответов выберите единственный правильный, результат занесите в бланк ответов.

А1. На координатной прямой отмечены точки А, В, С и D.

Числу  соответствует точка:

1)    А            2)  В            3)  С              4) D

А2. Известно, что у = 4,9 ± 0,3. Точное значение у не может быть равно:

1)    4,6            2)  5,2          3) 5,3           4)  4,7

А3. Сумма значений выражений   равна:

1)    40             2)  37,2          3) 34,2         4)  41

А4. Пропущенное число в равенстве 7 + … = 123 + (8 - …) равно:

1)    – 62         2)   61          3)   62           4) – 61

А5. На плане города улицы обозначенные как AB и CD, параллельны (рис. 35). Улица EF составляет с улицами AB и AC углы соответственно a=43° и b=65°. Найдите углы, которые образуют между собой улицы AC и AB, AC и CD.

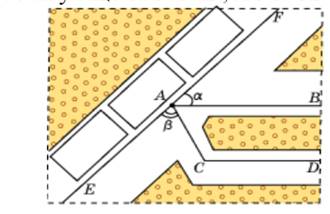
1)    72⁰, 108⁰               2) 72⁰, 98⁰                 3) 36⁰, 108⁰               4) 65⁰, 43⁰

А6. Большим корнем уравнения  является число:

1) 3                  2) 1,5                 3) -1,5              4) -3

А7. Значение дроби  равно:

1) 125                 2) 25               3) 625              4) 20

А8. На диаграмме показано количество посетителей сайта любителей кошек во все дни с 21 по 30 мая 2009 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей превышает наименьшее количество посетителей за день (в указанный период).

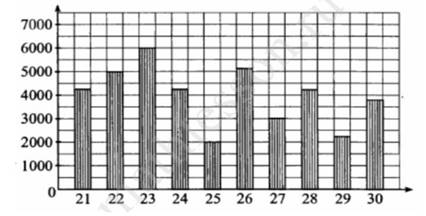
1)    1                    2) 2                    3) 3                  4) 4

А9. Выражение   :   , можно представить в виде дроби:

1)                       2)          3)                   4) 

А10. Книжный магазин делает скидку школьникам на определенное  количество процентов от стоимости покупки. Учебник стоит в магазине 816 рублей, школьник заплатил – 718 рублей 8 копеек. Скидка для школьников составит: (Ответ в %)

1)    97,92        2)     88        3)79,90272            4)12                                                         

А11. В прямоугольнике ABCD: _<BDC = 60⁰  , CD=8. Длина диагонали АС равна:

     А                            В

     D                          C

1) 4                 2) 8                         3) 10                   4) 16

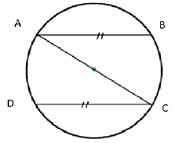А12. На рисунке AB=CD, AB=, AD= 9, AC=13 . По данным чертежа найти длину  отрезка DВ.

1)4,5                        2)    9                           3) 22                     4)  13

А13. Сумма выражений  и   равна:

1)  8                   2)                3) 0                 4) 4

А14. Наименьшим целым решением неравенства   -2 <  < 17 является число:

1)10                 2)9                  3)-8                 4)-9

А15. Число n = ·0,48 – (-1)³  заключено между соседними числами:

1) -1 и 0            2)1 и 2         3)0 и 1       4)-2 и -1

Часть 2

Указание 2: При выполнении задания В1 установите соответствие. Для каждой позиции, записанной под буквой, надо подобрать соответствующий номер ответа и вписать полученный результат в таблицу бланка ответов. Каждой букве соответствует только одна цифра.

В1. Установите соответствие между графиками функций и формулами, которые их задают.

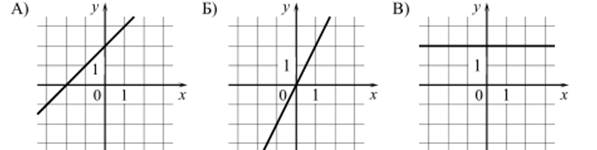ГРАФИКИ

ФОРМУЛЫ

2)    у = 2х                   2) у = х + 2                3) у = 2

В таблице под каждой буквой укажите соответствующий номер.

Ответ:

Указание 3: Для заданий В2 – В5 впишите правильный ответ в бланк ответов. На оборотной стороне бланка ответов приведите развернутое решение.

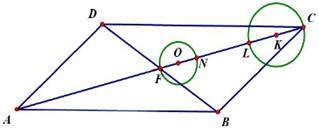
В2. Согласно рисунку: ABCD – параллелограмм

КС = 2FО, NL – FN = 6cм,

FC – NL = 24 cм.

Определите длину диагонали АС.

(Ответ в см)

В3.  Определите, при каких значениях параметра b уравнение х² + bx + 9 = 0  имеет единственный корень. Для каждого значения параметра b укажите соответствующий корень уравнения. В ответ впишите значение параметра b, удовлетворяющее условию: b < х, где х – соответствующий корень уравнения.

В4. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 18, 15 и 20. Найдите площадь четвёртого прямоугольника.

В5. Решите систему уравнений: .  В ответ впишите решение системы, принадлежащее III четверти системы координат.

ОТВЕТЫ

РАЗВЕРНУТОЕ РЕШЕНИЕ ЗАДАНИЙ В2 – В5

В2

Решение

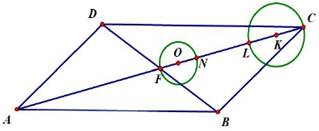
Пусть FO = х, тогда FN = KC = 2х,

NL = 4 + FN = 6 + 2х,

FC = 24 + NL = 24 + 6 + 2х = 30 + 2х.

С другой стороны FC = х + х + 6 + 2х + 2х + 2х =

= 8х + 6.

Получаем уравнение: 30 + 2х = 8х + 6, откуда х =4.

Тогда FC = 30 + 2*4 = 38, АС = 2*38 = 76.

Ответ: 76

В3  

Решение

Квадратное уравнение имеет один корень, только когда дискриминант равен нулю. Значит,  х² + bx + 9 = 0
D = b² - 4 × 1 × 9 = b² - 36
 b² - 36 = 0
b1 = 6 ; b2 = -6
 Если b = 6, то   х² + 6х + 9 = 0
                              (х + 3)² = 0                              6 > -3
                               x = -3                         

Eсли b = -6, то  х² - 6х + 9 = 0
                            (х - 3)² = 0                               - 6 < 3
                             х = 3
Ответ: - 6

В4

Решение

Введём обозначения, как показано на рисунке. Площадь верхнего левого прямоугольника равна 18, поэтому ас = 18, аналогично bc = 15, bd = 20. При помощи полученной системы уравнений выразим значение  ad:

 ;

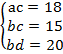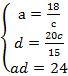
Из третьего уравнения получаем, что искомая площадь равна 24.

Ответ: 24.

В5

Решение

;

Решим 1 уравнение системы: