Статья на тему: "Некоторые свойства пространственных четырехугольников"

Статья

на тему:

«Некоторые  свойства   пространственных  четырехугольников»

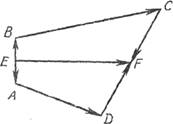
Задача 6. Доказать, что если АВСD — пространственный четырехугольник, т. е. четырехугольник с вершинами, не обязательно

лежащими в одной плоскости, то  +  = 2, где Е и F — сере­дины соответственно сторон АВ и DС.

Решение. Если ввести в рассмотрение векторы, указанные на рисунке 2, то можно составить следующие два равенства:

=  + +

  =  +  +

 Складываем их почленно и учтем, что  = -   и  = -  получим:                 

                        +  = 2    ( 6 )

       Пользуясь этим соотношением, получаем как частный случай

известную теорему: средняя линия трапеции параллельна основаниям, длина ее равна полусумме их длин.

 Для трапеции векторы  и  в равенство (6) коллинеарны, поэтому вектор 2ЕF коллинеарен соответственно им. Таким образом, средняя линия трапеции параллельна основаниям. Остается доказать, что ее длина равна полусумме длин оснований. Векторы  и сонаправлены, отсюда следует следующее равенство:

Подставляя в равенство ( 6 ) получи:    =

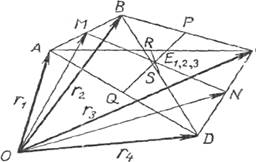
Задача 7. В пространственном четырехугольнике АВСD проведены три отрезка, соединяющие соответственно: 1) середины двух противоположных сторон; 2) середины двух других сторон; 3) середины диагоналей. Доказать, что эти три отрезка пересекаются в одной точке и каждый из них этой точкой делится пополам.

Решение.   Зафиксируем   точку О и  векторы  ,  ,  и  обозначим соответственно через r₁, r₂, r₃  и r₄ (рис. 3 ).  Пусть, далее, Е₁ — середина отрезка МN, Е₂ — середина PQ и E₃ – середина RS

 Выразим векторы _{1, 2} и ₃ через векторы r₁, r₂, r₃, r₄ . Так как точка Е₁ - серединой отрезка МN, то согласно лемме ( 1 ) 

              ₁ =

Точки M и N являются серединами соответственно отрезков  и , поэтому:

                          =    и  =    .  В результате получаем:

                       ₁ =

         Проводя   аналогичные    рассуждения для векторов                            ОE₂ и ОЕ₃, получим:

     OE₂ = OE₃  =

        Из равенства следует, что ОЕ₁ = ОЕ₃ = ОЕ₃. Отсюда следует,   что точки E₁ Е₂, Е₃ совпадают.  Задача решена.

             3. Некоторые свойства тетраэдров.

Задача8.  Показать,  что угол  θ     между   противоположными  ребрами тетраэдра вычисляется по формуле:

            Cos θ =      ( 7 )

где а к а' — длины рассматриваемых ребер, а Ь и Ь'  с и с' — длины двух других пар противоположных ребер.

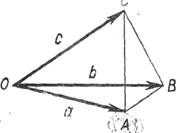
Решение. Пусть ОАВС — данный тетраэдр, а ОА  и ВС — рассматриваемые ребра (рис. 29). Введем обозначения:

 = а,  = b,  = с,  | | = a,  = Ь,  = с,  = а', AС = Ь', АВ = с'.

Искомое соотношение (7) может быть записано следующим образом:

       2aа' соs θ = с² + с'² — Ь² — b'²,   или

      2а*  = c² – b² + ²

       2a ( c – b ) = с² — b² + (Ь — а)² — (с — a)².

Воспользовавшись распределительным свойством скалярного произведения,  убедились в справедливости последне­го, а следовательно, н исходного соотношений.

Задача9. Доказать, что если в тетраэдре две пары противо­положных ребер взаимно перпендикулярны, то и третья пара ребер также взаимно перпендикулярна.

Д о к а з а т е л ь с т в о. Пусть ОАВС — данный тетраэдр, у ко­торого ОА ⊥ СВ и 0В ⊥ АС (рис. 29). Требуется доказать, что

ОС ⊥ АВ. Для решения задачи введем в рассмотрение векторы

  = а, = Ь и =с и запишем данные условия, используя скаляр­ное произведение векторов. Так как ОА⊥ СВ, то   •  = 0 или

а (Ь — с) = 0. Так как 0В ⊥ АС, то  •  = 0 или Ь (с — а) = 0. Сложив эти два соотношения, получаем аЬ — ас + Ьс — аЬ = 0, с (Ь— а) = 0, т. е.  •  = 0. Отсюда следует, что прямые ОС и АВ взаимно перпендикулярны.

Учитель математики ГКОУ РД «РЦДОДИ»     Гаджимирзаев М.М.