Статья "Применение математических знаний и умений при изучении дисциплин профессионального цикла"

Применение математических знаний и умений при изучении дисциплин профессионального цикла

Математику только затем учить надо,

 что она ум в порядок приводит

Ломоносов

Развитие всех направлений нашего общества немыслимо без математического образования и математической грамотности. Математическая подготовка является полноправной и важной составляющей среднего профессионального образования, и осуществляется она  в соответствии с требованиями государственного образовательного стандарта и реализацией образовательных программ.

Изучение математики в колледже на разных уровнях (I-II курсах), создает фундамент математического образования, необходимый для получения общих и профессиональных компетенций, воспитывает математическую культуру и понимание роли математики в различных сферах профессиональной деятельности.

Основные знания и умения, которыми должен овладеть обучающийся в процессе изучения математики, отражают требования к уровню обучения. Обучающиеся должны знать основные определения математических понятий, формулировки теоретических фактов, а также овладеть умениями как общего, так и частного характера.    В результате  изучения математики, обучающиеся должны усвоить, что математические понятия и факты, обладая большой общностью, имеют широкое применение.       Особенностью  заданий является  прикладная направленность.  Эти задания направлены на формирование у студентов навыков построения и исследования математических моделей реальных процессов, они должны способствовать выработке стиля логического мышления, критического мышления необходимого специалисту.

Применение математических знаний и умений в дисциплинах профессионального цикла                                             

     Некоторым обучающимся  не очень понятна необходимость математики в дальнейшем обучении по выбранной специальности. Они часто задают вопросы – Для чего нужны  логарифмы, показательная, тригонометрические функции,  пределы,  производная функции, дифференциальные уравнения, и прочее? Что такое «математический аппарат»?  Как они влияют на нашу жизнь?   

Простой пример:  обучающиеся пишут контрольную работу по теме «Показательная и логарифмическая функция»:  строят графики функций, решают уравнения, неравенства, потенцируют или  логарифмируют выражения.  Решили в пределах математических правил – получили оценку (предположим  положительную). Результат повлиял на промежуточную (или итоговую аттестацию). Вышел на стипендию.  И что это все – предел, с которым ты справился?

Иное дело (абстрактный пример) – технология программирования: предположим, что при программировании обучающийся описывает какую-либо функцию, которая впоследствии будет давать практическую пользу на каком-либо предприятии. Обучающийся чувствует удовлетворение, когда готовая программа даст  результат –  реальная польза от программы.

    Поэтому,  мотивация познавательной деятельности  на занятиях  «Математика»   - это необходимая психологическая подготовка обучаемого к восприятию изучаемого материала. Для повышения интереса к  математическим дисциплинам преподаватели  учитывают ведущие группы мотивов: интерес к знаниям, к процессу их приобретения; показ практической и теоретической значимости изучаемого материала; создание ситуации успеха в выполнении учебного задания; оценка знаний.

   Применение математики  к любой практической проблеме начинается с построения математической модели.  Известно, что начало – это половина дела. Имея задачу, сформулированную математически, можно выбрать алгоритм ее решения. Т.е. обучающийся должен уметь  строить и анализировать математические модели,  выбирать метод решения.

Например,

СХЕМА МАТЕМАТИЧЕСКОГО РЕШЕНИЯ

ЭКОНОМИЧЕСКОЙ ЗАДАЧИ

ЭКОНОМИЧЕСКАЯ ЗАДАЧА – представляет собой некоторую экономическую модель данного экономического процесса;

↓

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА -  данной экономической модели ставится в соответствие некоторая математическая модель, т.е. данная экономическая модель интерпретируется в виде математической задачи;

↓

МЕТОД РЕШЕНИЯ – выбор метода решения, исходя из анализа математической задачи;

↓

ПРОЦЕСС РЕШЕНИЯ – точное и последовательное применение, выбранного метода решения;

↓

ЭКОНОМИЧЕСКАЯ ТРАКТОВКА РЕЗУЛЬТАТА – экономическая трактовка численного результата, полученного в результате решения математической задачи.

Приведем примеры использования обучающимися математических знаний и умений.

Технические специальности

Раздел:   Линейная алгебра

1. Определение силы тока І₁ ,  І₂ ,  І₃  в электрической цепи с заданным НДС  (по второму закону Киргоффа) сводится к решению системы линейных уравнений  (методом Крамера, методом Гаусса)

                                 5 І₁+3I₂ + І₃  =7

                                 4 І₁-2I₂ –3І₃=3

                                  І₁ +І₂ + І₃ =3

Раздел:  Математический анализ

Тема - Комплексные числа

     Ряд наук применяют  комплексные числа. Тема «Комплексные числа» - одна из ведущих прикладных тем курса высшей математики для технических специальностей, ее содержание углубляется в общетехнических дисциплинах  техникума (студенты выполняют построение  кривой  и вектора по уравнению синусоиды, построение вектора по комплексному числу,   определяют комплексное число по вектору и уравнению,  определяют уравнение по комплексному числу, т.е. при расчетах цепей приходится проводить математические операции с комплексными числами).  Также, учитывая, что во многих материнских платах современного компьютера используются знания о комплексних числах – благодаря им существует ряд дополнительных возможностей в наших компьютерах, то комплексные числа  используются также в  ряде компьютерных  дисциплин.

      1. Величина силы  тока  электрической цепи вычисляется по формуле .   Найти силу тока, если   

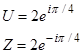
2.  Полное сопротивление ЛЭП (линии электропередач) после включения  тока вычисляется по формуле  Z=U/I.Определить сопротивление, если U = 2i,  I = 1 - i. Результат записать в показательной форме.

3. Напряжение в обмотке  трансформатора вычисляется по формуле U = I*Z. Найти напряжение U,             если  I  = 4e^і20°,    Z = 10e^і70°. Результат записать в тригонометрической и алгебраической формах.

4. Найти сопротивление Z первичной обмотки трансформатора, если              U =  4 + 2i,   I = 1 + 3i,  Z=U/I. Результат записать в тригонометрической и показательной  формах.

5. Сила струму, которая проходит по первичной обмотке  асинхронного двигателя, представлена в комплексной форме  I  = 2 + 2i,  напряжение  -       U =3(cos90° + i sin90°). Найти сопротивление первичной обмотки трансформатора, если Z=U/I.

ЗАКЛЮЧЕНИЕ

     Области применения математики практически не ограничены.   Базовыми навыками математического мышления способен овладеть каждый.  

     Овладение математическими знаниями и умениями обучающимися  поможет в изучении смежных естественно-научных дисциплин на базовом уровне и дисциплин профессионального цикла. Задача преподавателей математики техникума состоит в том, чтобы вооружить студентов основами математических знаний  и умений в том объеме, который необходим в их повседневной жизни, в практической деятельности и для сознательного усвоения дисциплин профессионального цикла, а также достаточен для дальнейшего повышения квалификации путем самообразования.