Статья "Реализация обучения через разноуровневый, дифференцированный, индивидуальный подход к обучающимся с ОВЗ в начальной школе на уроках математики (из опыта работы)"

Реализация обучения через разноуровневый, дифференцированный, индивидуальный подход к обучающимся с ОВЗ в начальной школе на уроках математики (из опыта работы)

Автор: Картавцева Е.О., учитель начальных классов МОУ «С(К)ОШИ №4» г. Магнитогорска, Челябинская область

  Индивидуализация обучения обусловлена тем, что уровень подготовки и развития способностей к учению не у всех школьников одинаков. Учащиеся, собранные вместе только по возрастному принципу без учета их интеллектуальных и индивидуальных способностей, не могут равномерно и одинаково продвигаться вперед в усвоении знаний. Ученики одного итого же класса для выполнения одного и того же задания могут тратить от 5 минут до 1,5 часов. Ученики, которые не обладают для данного возраста гибкостью, подвижностью мышления, умением обобщать, творчески подходить к решению тех или иных задач, начинают отставать в прохождении учебного материала. У таких учеников снижается  интерес к знаниям, проявляется отрицательное отношение к учебе, что приводит к неуспеваемости. Не лучше положение и с сильными учениками, которые вынуждены работать не в полую силу своих возможностей в связи с тем, что учитель организует ход обучения, ориентируясь на «среднего» ученика. Они постепенно привыкают к легкости выполнения учебных заданий, и первые трудности порождают растерянность, неуверенность в себе. А это ведёт к снижению успеваемости.

Поэтому задача достижения максимально высокой успеваемости каждым       учеником может быть решена только на основе индивидуально-ориентированной системы обучения, при дифференцированном подходе, который позволяет учитывать индивидуальные особенности ребенка, создавать условия для преодоления и развития его потенциальных возможностей, а также позволяет сделать учебный процесс  более эффективным.

Понятие дифференциации образования тесно связано с созданием оптимальных условий для развития личности, наиболее полного учета, как индивидуальных различий детей, так и социальных и культурных факторов, присущих каждой конкретной школе и ее окружению.

Дифференциация обучения – это подход к организации учебной деятельности, при котором обеспечивается учет индивидуальных возможностей детей. Дифференциация является звеном, частью, средством индивидуального подхода, что можно увидеть на схеме: Схема 1

Дифференцированная работа упорядочивает деятельность учителя, т.к. позволяет применять методы не для каждого ребенка в отдельности,  а для определенной категории учащихся.

На уроке математики дифференцированный подход предполагает вариативность темпа обучения, выбор разных видов деятельности, определение характера и дозировки помощи со стороны учителя. Класс делится на группы, с целью осуществления учебной работы с ними на разных уровнях с использованием разных методов обучения. При этом дифференциация направляется не только на детей, испытывающих трудности в обучении, но и на одаренных школьников.

Таким образом, класс можно разделить на сравнительно одинаковые по уровню обучаемости группы по следующей схеме:

1-я группа – учащиеся с высокими учебными способностями, выполняющими работу большей сложности, требующие умения применять знания в незнакомой ситуации и самостоятельно творчески подходить к решению учебных задач.

2-я группа – учащиеся со средними способностями, выполняющие задания первой группы, но с помощью учителя или опорных схем, или после разъяснения сильными учащимися.

3-я группа – учащиеся с низкими учебными способностями, требующие точного ограничения учебных заданий, большого количества тренировочных работ и дополнительных разъяснений нового на уроке.

Класс делится на разноуровневые группы, где учитываются различные уровни усвоения знаний учащимися (См. табл. 1).

Таблица 1

При дифференцированном процессе обучения группы имеют временный состав, т. е. возможен переход учащихся из одной группы в другую. Переход обусловлен изменением в уровне развития ученика, скоростью выполнения пробелов и повышением учебной направленности, выражающейся в появлении интереса к получению знаний в учебе.

Дифференциацию обучения обычно реализуется через использование дифференцированных заданий.

Дифференцированные задания – система упражнений, выполнение которых поможет каждой группе учащихся глубоко и осознанно освоить правила и выработать необходимые вычислительные навыки, сформировать мыслительные действия.

Задания подготавливаются к уроку заранее: записываются на доске или на индивидуальных карточках. Задания можно разделить на три вида:

I          Обязательные задания. Они способствуют умению правильно применять изученное правило для выработки вычислительного навыка. Количество их должно быть ограниченным. Задания должны быть посильны для каждого ученика.

II                 Дополнительные задания. Эти задания рассчитаны на тех детей, которые справились с обязательными заданиями и у них остается время для самостоятельной работы. Это задания повышенной трудности, на применение изученного правила, требующие сравнения, анализа и синтеза.

III                   Творческие задания.  Такие задания предлагаются учащимся, выполнившим дополнительные задания без особых затруднений. Они способствуют активизации творческих способностей.

Обязательные, дополнительные  и творческие задания  могут применяться на любом этапе урока, но чаще всего, дифференцированные задания используются на этапе закрепления нового материала, при этом схема деятельности педагога может строиться следующим образом (См. схему 2):

Схема 2

Основной чертой, характеризующей дифференцированные задания  для самостоятельной работы, является наличие вспомогательных средств, оптимально приспосабливающих обучение математике  к динамике усвоения знаний, формирования умений и навыков у учащихся различных категорий.

Обязательные дифференцированные задания можно разделить на следующие виды:

1.          Задания с наличием образца выполнения. Для формирования вычислительного навыка необходимо развернутое объяснение. Задания с наличием образца выполнения представляют рассуждения, на основе которых можно решить ряд примеров.

2.          Задания с выполнением некоторой их части. Учащимся предлагаются задания, решение которых нужно закончить. Причем в готовом виде даются те части решения, которые на определенной ступени представляют трудность для школьников. Подобные задания помогают учащимся перейти от частично самостоятельной работы к вполне самостоятельной.

3.          Задания с сопутствующими указаниями, инструкциями. На первых этапах усвоения способа решения примеров используются задания с указаниями и советами частного характера, определяющими выбор способа действия. Далее даются задания с общими указаниями, применимыми к решению примеров и задач любой математической структуры. 

4.                Задания с теоретическими справками. Цель таких заданий – учить обосновывать выбор того или иного действия, контролировать свои вычисления, соотнося их с правилом.

В качестве дополнительных дифференцированных заданий можно использовать следующие:

5.                            Работа с дополнительными источниками информации. После выполнения самостоятельных заданий учащихся можно познакомиться с другими формулировками: записями правила, вычисления или приема.

6.                            Задания конструктивно-вариативного содержания. Эти задания являются прямым продолжением обязательных заданий. Например, если с помощью обязательных заданий формировали вычислительные навыки, то продолжением могут быть наблюдение за изменением результата, составление таблиц, рядов чисел, нахождение лишних элементов и т. д.

Задания творческого характера требуют от учащихся проявления смекалки, фантазии. Это могут быть следующие задания:

1.     Расположение решенных примеров в определенном порядке (возрастания или убывания).

2.     Придумывание своих примеров, содержащих определенную закономерность.

3.     Составление задачи по данному выражению.

4.     Составление задачи, обратной данной и т.д.

Чаще всего дифференцированные задания для самостоятельной работы предлагаются на карточках. Зная особенности учеников, учитель всегда может определить вариант работы для группы. В системе упражнений, переходя от работ под непосредственным руководством учителя к частично самостоятельной работе и далее к вполне самостоятельной, учащиеся последовательно справляются с заданиями разных уровней сложности. Трудность задания и степень самостоятельности постепенно нарастает, что позволяет реализовать дидактический принцип – продвижение в развитии всех учеников, имеющих различные учебные способности.

          Таким образом, используя дифференцированный подход в обучении, каждый ученик имеет возможность овладевать учебным материалом по предмету на разном уровне, но не ниже базового, в зависимости от его способностей и индивидуальных особенностей личности. Цель применения дифференцированных заданий – обеспечение наиболее целесообразного характера деятельности каждого учащегося в процессе самостоятельной работы на уроке с учетом индивидуальных особенностей (уровень подготовленности, особенности мышления, памяти, интересы, склонности). Поэтому для учащихся с более низкими учебными способностями необходимо предлагать задания, позволяющие повысить активность в процессе восприятия, осмысления нового материала, оказывать им оперативную помощь при первичном закреплении материала, учить приемам рациональной умственной деятельности, способствовать систематизации и совершенствованию знаний. А для учащихся с более высокими учебными способностями – задания, требующие посильного умственного напряжения, большей самостоятельности, творческого поиска правильных способов решения.

Организация дифференцированного обучения предполагает следующую деятельность учителя:

Ø определение содержания учебного материала;

Ø распределение материала по блокам;

Ø разработка заданий разноуровневого характера;

Ø анализ результатов.

Реализуя уровневую дифференциацию, прежде всего, каждый учитель должен учитывать, что необходимым является четкое определение минимума, без которого ученик не сможет двигаться дальше в изучении данного предмета,  т.е. уровень общих требований, который должен выполнять каждый ученик.

В соответствии с содержанием учебника весь программный материал разбивается на крупные блоки. Далее, исходя из содержания блока, подбираются задания для самостоятельной работы. Форма предъявления задания может быть различна. Задание может предлагаться не только на отдельной карточке, но и в записи вариантов на доске или по учебнику. При этом возможны любые удобные для учителя и целесообразные для учащихся виды сочетания этих форм. Например, одна группа работает с заданиями по карточкам, другая по заданиям, записанным на доске, третья – по учебнику.

Задания, предлагаемые на карточках, носят комплексный характер, т. е. в одном и том же виде карточек имеются в наличии элементы помощи и усложнения. В данном случае весь класс работает по одному виду карточек, но при этом каждый выполнят посильную для себя часть.

Планируя урок, на котором предполагается самостоятельная работа, учитель намечает задания для учащихся в соответствии с имеющимися на данный момент уровнем знаний, умений и навыков, определяет меру своего руководства индивидуальной работой учащихся. Перед началом самостоятельной работы в классе необходимо проинструктировать учащихся, сообщить им, какие требования предъявляются к выполнению работы, каков порядок ее выполнения. Общие указания следует давать до тех пор, пока учащиеся не приобретут навык самостоятельной работы над заданием.

В соответствии с содержанием учебника по математике (авторы И.И.Аргинская, Е.И.Ивановская), весь программный материал разбит на следующие блоки:

Блок-1. Нумерация чисел в пределах 100.

Блок-2. Изучение действий.

Блок-3. Элементы геометрии.

Блок-4. Работа с задачами.

По каждому блоку были разработаны дифференцированные задания.  Задания, предлагаемые на каждой из карточек,  содержат как элементы помощи, так и элементы усложнения (т. е. содержат задания трех уровней), что позволяет учащимся с  различными учебными способностями выполнять посильную для них работу.

Задания,  предлагаемые на карточках под цифрой 1, являются обязательными заданиями, которые способствуют умению правильно применять изученное правило для выработки вычислительного навыка.

Задания под цифрой 2 – дополнительные. Эти задания рассчитаны на тех учащихся, которые справились с обязательными заданиями, т.е. задания на применение изученного правила, требующие сравнения, анализа и синтеза.

Задания под номером 3 предлагаются учащимся, выполнившим дополнительные задания без особых затруднений. Эти задания носят творческий характер.

                 Блок-1.  Нумерация чисел в пределах 100

 Задания данного блока (они помечены на карточках сокращенно: Б-1), направлены на закрепление знаний об устной и письменной нумерации двузначных чисел, отработку навыков сравнения всех изученных чисел и представления двузначных чисел в виде суммы разрядных слагаемых. (См. прил.1).

Блок-2.  Изучение действий

В рамках этого блока (карточки с меткой Б-2) отрабатываются следующие умения:

a.                              складывать и вычитать  однозначные и двузначные числа на основе использования таблицы сложения, выполняя записи в строку и в столбик (данные умения основываются на понимании детьми поразрядности выполнения сложения и вычитания);

b.                             выполнять умножение и деление в пределах табличных случаев на основе знания таблицы умножения;

c.      находить значения сложных выражений, содержащих 2 – 4 действия.

Цель заданий этого блока – формирование вычислительных навыков. (См. прил. 2).

                     Блок-3.  Элементы геометрии

При изучении геометрического материала задания данного блока (карточки Б-3) помогут выработать следующие умения: находить длину ломаной и периметр произвольного многоугольника. (См. прил. 3).

                 Блок-4.  Работа с задачами

При решении заданий данного блока формируется умение решать текстовые задачи, что является важнейшим аспектом математического образования. Для учащихся с низким уровнем математических  способностей предлагаются задания, формирующие умение выделять в задаче условие, вопрос, данные и искомое; выбирать действия для решения простой задачи на любое из четырех арифметических действий. Для более сильных учащихся предлагаются задания на выполнение краткой записи задачи, используя условные знаки; составление задач, обратных данной; выбор действий при решении составных задач. (См. прил. 4). После того, как учащиеся приобретут навыки самостоятельной работы по карточкам, можно предлагать разноуровневые задания в форме записи на доске  на выбор учащимся, т. е. уровень сложности задания ученик выбирает сам.

Оптимально приспособить задания к уровню знаний, умений и навыков невозможно без их систематического учета. Проверяя самостоятельные работы и выставляя отметки, следует учитывать, что на данный момент освоил ученик, и что еще предстоит освоить в ближайшее время. Результаты работы необходимо фиксировать, выделяя общие характерные особенности способа действия и определяя виды заданий для последующей работы с группой.

Используя словесную оценку, учитель должен учитывать индивидуальные особенности учащихся, создавать положительный эмоциональный настрой во время проверки  знаний и умений, сравнивать полученный результат ученика с его предыдущим личным результатом.

При выставлении отметки следует учитывать различные уровни усвоения знаний учащимися.

Первый уровень - репродуктивный. Воспроизведение и запоминание. Связано с непосредственным воспроизведением содержания изученного материала различной сложности.  Отметка « 3 ».

Второй уровень – практический. Применение знаний в знакомой ситуации по образцу. Выполнение действий с четко обозначенными правилами. Применение знаний на основе обобщаемого алгоритма (схемы). Отметка « 4 ».

Третий уровень – творческий. Применение знаний в незнакомой ситуации, творческое решение учебных задач. Отметка « 5 ».

Для организации контроля по эффективности применения дифференцированных заданий на уроках математики, в течение текущего учебного года результаты проверочных работ по предмету фиксировались, где учитывался уровень усвоения знаний учащимися. Обобщенные результаты за I и III четверти показали, что в уровнях освоения знаний и применения их на практике учащимися происходило развитие (см. рис. 1 и 2):

Рисунок 1.

I четверть

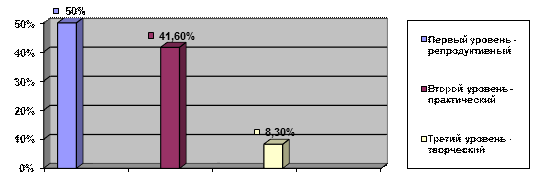
Рисунок 2.

III четверть

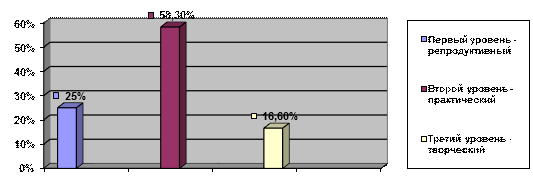
На рисунках 1 и 2 можно проследить продвижение в развитии учащихся, имеющих различные уровни усвоения знаний, т.е. с одного уровня многие учащиеся перешли на другой уровень – более высокий.  Данный переход был обусловлен организацией и применением дифференцированного подхода к учащимся, что отразилось и на их успеваемости.

Из вышесказанного можно сделать вывод, что применение дифференцированного подхода  на уроках математики способствует не только  достижению высокого уровня знаний, усвоению программного материала на уровне способностей каждого учащегося, но и созданию благоприятных  морально-психологических условий обучения и развития  у младших школьников, способствующих формированию предметного и познавательного интереса в общем.

Приложение 1

Приложение 2

Приложение 4