Далеко, далеко, на лугу пасутся ко...

Трава на лугу растёт равномерно. Известно, что 30 коров съедают всю траву за 60 дней, а 70 коров – за 24 дня. Сколько коров съедят всю траву на лугу за 96 дней?

Ответ – в графике

Пользуясь графиком, определите:

1)           какое расстояние проехал мотоциклист за первый час движения?

2)           на каком расстоянии от дома находится дача? Сколько времени мотоциклист находился на даче?

3)           на каком расстоянии от дома мотоциклист остановился отдохнуть на обратном пути? Сколько времени продолжалась эта остановка?

4)           на каком расстоянии от дома был мотоциклист через 5 ч после начала движения?

5)           с какой скоростью двигался мотоциклист последние полчаса?

Возьмут ли тебя на работу в крупную известную фирму?

Вот 4 вопроса, которые используют кадровые агентства мирового уровня для того, чтобы оценить умственные способности кандидатов:

Вопрос 1: Как засунуть жирафа в холодильник?

Этот вопрос позволяет выяснить, нет ли у вас склонности выискивать чересчур сложные решения для простых задач.

Вопрос 2: Как засунуть в холодильник слона?

Этот вопрос позволяет выяснить, способны ли вы при принятии решений учитывать последствия ваших предыдущих действий.

Вопрос 3: Лев созвал всех зверей на собрание. Явились все, кроме одного. Что это за зверь?

Этот вопрос проверяет вашу память.

Вопрос 4: Вам нужно пересечь широкую реку, которая кишит крокодилами. Как вы это сделаете?

Этот вопрос позволяет выяснить, способны ли вы учиться на собственных ошибках.

Решение

Это одна из красивых арифметических задач, которые хотя и можно решить составлением уравнения, но намного красивее – сделать это с помощью последовательных рассуждений.

Итак, известно, что:

30 коров за 60 дней съедят всё поле и ту траву, которая на нём вырастет за 60 дней

70 коров за 24 дня съедят всё поле и ту траву, которая на нём вырастет за 24 дня.

Следовательно:

Всей травы на поле и той, что вырастет на нём за 60 дней, одной корове хватит на 30*60=1800 дней.

Всей травы на поле и той, что вырастет на нём за 24 дня, хватит одной корове на 70*24=1680 дней.

Отсюда, травы, которая вырастет на поле за 60-24=36 дней, хватит одной корове на 1800-1680=120 дней.

Значит всей травы на поле и той, что вырастет на нём за 60+36=96 дней, хватит одной корове на 1800+120=1920 дней

А то, что одна корова съест за 1920 дней, за 96 дней съедят 1920/96=20 коров.

Ответ За 96 дней всё поле съедят 20 коров. http://intelmath.narod.ru/problem_cows.html  за первый час движения мотоциклист проехал 60 км

•      дача находится от дома на расстоянии 120 км;

•      3 ч − 2 ч = 1 ч мотоциклист находился на даче.

•      на расстоянии 75 км от дома мотоциклист остановился отдохнуть на обратном пути;

•      4,5 ч − 4 ч = 0,5 ч = 30 минут продолжалась эта остановка.

•      через 5 часов после начала движения мотоциклист был в 60 км от дома

•      45 км проехал мотоциклист за последние полчаса, следовательно: v=S:t=45:0,5=452=90 км/ч скорость мотоциклиста в последние полчаса движения. https://reshalka.com/uchebniki/7-klass/algebra/merzlyak/767

Оптические иллюзии

Смотрите на точку в центре и одновременно приближайте к ней голову.

Насколько сложной может быть задача, составленная на материале начальной школы: сложении, умножении, делении и чётности/нечётности числа?

Оказывается, более 70 лет назад Лотарем Коллатцем сформулирована так называемая проблема «3x+1», над которой бились математики лучших университетов мира, потрачены миллионы часов машинного времени,   но           никакие         усилия           к окончательному решению не привели.

В то же время понять условие этой задачи может даже первоклассник. Оно звучит так:

Возьмём какое-нибудь натуральное число. Далее, если число чётное, разделим его на 2, а если нечётное – умножим на 3 и прибавим 1. Затем будем выполнять эти действия с полученным числом.

Например, вот что будет происходить, если начать с пятёрки.

5           5+1=16       16:2=8      8:2=4       4:2=2       2:2=1

     3+1=4      4:2=2     2:2=1  Круг замкнулся. Теперь мы будем постоянно получать значения 1 – 4 – 2.

Требуется узнать, существует ли такое число, начав с которого не скатишься к единице?

Современная математика не в силах дать ответ на такой, казалось бы, простой вопрос. Даже недавно доказанная великая теорема Ферма – и та формулируется с использованием возведения в степень и целых четырёх переменных. А для задачи 3x+1 на сегодня достоверно известно, что последовательность приходит в единице для всех не более чем девятнадцатизначных чисел, но в общем случае это ничего не доказывает. Есть даже предположение, что проблема 3x+1 – одно из так называемых «недоказуемых» утверждений, существование которых следует из теоремы Гёделя о неполноте.

Однако проследить за поведением отдельных чисел при таком преобразовании – само по себе интересное математическое развлечение. Берём число и начинаем из него по приведённому правилу начинаем получать следующие. Попутно можно замечать, до какого максимума удалось подняться и сколько шагов придётся сделать, пока не придём к единице.

Математики шутят

На помощь русскому языку приходит математика

Соседи

Некоторые утверждают, что эта загадка была составлена Эйнштейном в детстве, и что 98% людей не сумеют решить эту задачу.

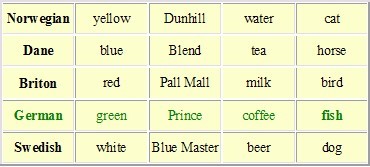
На улице стоят 5 домов разного цвета. В каждом доме живёт человек другой национальности. У каждого есть свой любимый напиток, каждый предпочитает свою марку сигарет и у каждого есть своё отличное от всех других домашнее животное.

1.    Англичанин живёт в красном доме.

2.    Швед держит собаку.

3.    Датчанин пьёт чай.

4.    Зелёный дом стоит рядом с белым домом, слева.

5.    Хозяин зелёного дома любит кофе.

6.    Человек, который курит “Pall Mall”, разводит птиц.

7.    Владелец жёлтого дома предпочитает курить “Dunhill”.

8.    Человек, живущий в доме посередине, пьёт только молоко.

9.    Норвежец живёт в первом доме.

10.Человек, который курит “Blends” живёт по соседвству с владельцем котов.

11.Хозяин лошади живёт по соседству с курильщиком “Dunhill”.

12.Тот кто курит “Blue Master”, пьёт пиво.

13.Немец предпочитает сигареты “Prince”.

14.Дом норвежца стоит рядом с голубым домом.

15.Один из соседей курильщика “Blends” пьёт только воду.

Кто разводит рыбок?

Вы относитесь к 2%, которые могут решить эту задачу?

Новости из мира математики

Математики нашли новое самое большое простое число. Об этом сообщили участники проекта Great Mersenne Prime Search. Визуально это число нельзя отразить, поскольку оно содержит 23 249 425 знаков, пишет «Федеральное агентство новостей». Для записи числа понадобилось бы 7 000 книжных страниц. В итоге математики обозначили число как M77232917, так как число есть степень двойки с показателем степени равным 77 232 917 минус один. Простое число делится на единицу и само себя. Начало последовательности выглядит следующим образом: 2,3,5,7, 11, 13, 17, 19, 23 и так далее. Добавим, что предыдущее самое большое простое число было открыто в январе 2016 года.