Степенная и показательная функции, их свойства и графики

Тема: Степенная и показательная функции, их свойства и графики

Повторить изученный материал

Степенная функция, ее свойства и график

Опр. Функция вида y=хⁿ, где n – любое число называется степенной функцией.

Примеры: y=х²    y=х³     y=х^-4   у=х^1/3

Свойства степенной функции и ее график зависят от показателя степени n.

1.  n – положительное четное число.

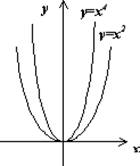
Примеры: y=x², y=x⁴, y=x¹⁰.

Графиком функции служит парабола, симметричная относительно оси OY. Свойства функции:

Df – область определения: х – любое число от -∞ до +∞

Еf – множество значений функции: y может принимать только неотрицательные значения [0;+∞)

Функция немонотонная, ограничена снизу, четная, непрерывная.

2.  n– положительное нечетное число.

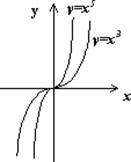Примеры: y=x³, y=x⁵,y=x¹³.

Графиком функции служит парабола, симметричная относительно начала координат. Свойства функции:

Df – область определения: х – любое число от  -∞ до +∞

Еf – множество значений функции: y - любое число от -∞ до +∞

Функция возрастающая, неограниченная, нечетная, непрерывная.

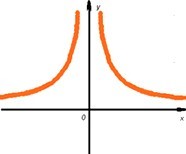
3. n – отрицательное четное число

Графиком функции служит кривая, симметричная относительно оси OY.

Свойства функции:

Df – область определения: х – любое число неравное нулю,

х ≠0 Еf – множество значений функции: y – (0;+∞)

Функция немонотонная, ограничена снизу, четная, не является непрерывная. 

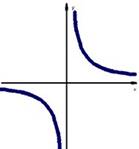
4.  n–отрицательное нечетное число

Графиком функции служит кривая, симметричная относительно начало координат.

Свойства функции:

Df – область определения: х – любое число, не равное нулю, х ≠0

Еf – множество значений функции: y – любое число, не равное нулю, y ≠0

Функция убывающая, неограниченная, нечетная, не является непрерывная.

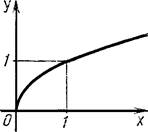
5.  n – в виде дроби, числитель которой равен единице, а знаменатель – положительное четное число

Графиком функции служит кривая, расположенная в первом координатном углу.

Свойства функции:

Df – область определения: х – любое неотрицательное число [0;+∞) Еf – множество значений функции: y – любое неотрицательное число [0;+∞)

6.  n – в виде дроби, числитель которой равен единице, а знаменатель – положительное нечетное число

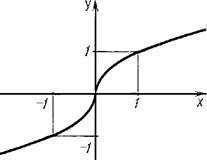Область определения этой функции – множество всех чисел Графиком функции служит кривая, симметричная относительно начало координат.

Свойства функции:

Df – область определения: х – любое число (-∞;+∞)

Еf – множество значений функции:  y любое число (-∞;+∞)

Функция возрастающая, неограниченная, нечетная, непрерывная.

Функция вида , где называется показательной функцией. Основные свойства показательной функции:

1. Областью определения показательной функции будет являться множество вещественных чисел.

2. Область значений показательной функции будет являться множество всех положительных вещественных чисел. Иногда это множество для краткости записи обозначают как R+.

3. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a

4. Справедливы будет все основные свойства степеней. Основные свойства степеней представлены следующим равенствами:

Данные равенства будут справедливы для все действительных значений х и у.

5. График показательной функции всегда проходит через точку с координатами (0;1)

6. В зависимости от того возрастает или убывает показательная функция, её график будет иметь один из двух видов.

На следующем рисунке представлен график возрастающей показательной функции: a>0.

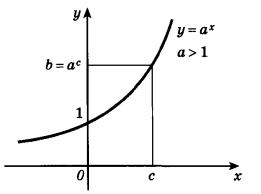
На следующем рисунке представлен график убывающей показательной функции: 0<a<1.

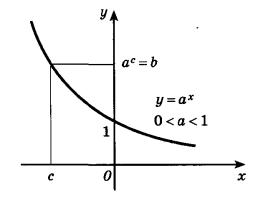
И график возрастающей показательной функции и график убывающей показательной функции согласно свойству, описанному в пятом пункте, проходят через точку (0;1).

7. Показательная функция не имеет точек экстремума, то есть другими словами, она не имеет точек минимума и максимума функции. Если рассматривать функцию на каком-либо конкретном отрезке, то минимальное и максимальное значения функция будет принимать на концах этого промежутка.

8. Функция не является четной или нечетной. Показательная функция это функция общего вида. Это видно и из графиков, ни один из них не симметричен ни относительно оси Оу, ни относительно начала координат.

V. Домашнее задание: Повторить свойства