Методы решения стереометрической задачи №14 

ЕГЭ профильного уровня

                                                                           Наука не является и никогда не будет                                                                                        являться законченной книгой.

                                                                                                                            А. Эйнштейн

      Большую роль в развитии геометрии сыграло применение алгебры к изучению свойств геометрических фигур, разросшееся в самостоятельную науку — аналитическую геометрию. Возникновение аналитической геометрии связано с открытием метода координат, являющегося основным ей методом. Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. 

 Существует множество систем координат: аффинная, полярная, биполярная, коническая, параболическая, проективная, сферическая, цилиндрическая и др. Наиболее используемая из них — прямоугольная система координат (также известная как декартова система координат). Ею мы и  пользуемся в школьном курсе геометрии. Данный метод решения заключается во введении (привязке к исследуемым фигурам) декартовой системы координат, а затем – исчислении образующихся векторов (их длин и углов между ними). Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций. Алгоритм применения метода координат к решению геометрических задач сводится к следующему: 

•        Выбираем в пространстве систему координат из соображений удобства выражения координат и наглядности изображения. 

•        Находим координаты необходимых для нас точек. 

•        Решаем задачу, используя основные задачи метода координат.

•        Переходим от аналитических соотношений к геометрическим.

В настоящее время уже очень большое число специалистов из разных областей науки имеют представление о прямоугольных декартовых координатах на плоскости, так как эти координаты дают возможность наглядно при помощи графика изобразить зависимость одной величины от другой. Название «декартовы координаты» наводит на ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты использовались в геометрии еще до нашей эры. Древний математик александрийской школы Аполлоний Пергский (живший в III-II веке до н. э.) уже фактически пользовался прямоугольными координатами. Он определял и изучал с их помощью хорошо известные в то время кривые: параболу, гиперболу и эллипс.

      Декарт внес в прямоугольные координаты очень важное усовершенствование, введя правила выбора знаков. Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру. Нужно сказать, однако, что одновременно с Декартом построил аналитическую геометрию и другой французский математик, Ферма. 

       Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.

        Метод координат – это универсальный метод. Он обеспечивает  тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.

        В отношении школьного курса геометрии можно сказать, что в некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи

более рационально, красиво, чем чисто  геометрический способ.                                      

Итак, задачи 14 из ЕГЭ – 2018. Какие же это задачи?

 Я бы хотела показать Вам разбор задач типа 14 двумя методами: вычислительноаналитическим и векторно-координатным. 

1) Задача на нахождение угла между двумя скрещивающимися прямыми.

• Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.

• 0˚ < (a;b)≤ 90˚ .

• Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.

• Две прямые называются перпендикулярными, если угол между ними равен 90˚ .

• Угол между параллельными прямыми считается равным нулю.

• При нахождении угла между прямыми используют:

1)   формулу  cosφ  =   для нахождения углаφ  между прямыми m и l , если стороны а и b треугольника АВС соответственно параллельны этим прямым;

                                                      | ∙ |                                                                                                   |    ∙            ∙            ∙   |

2)   формулу  cosφ  =            или в координатной форме       

| ̅|·| |

для нахождения угла φ между прямыми m и l , если векторы  ̅(х₁;у₁;z₁) и (х₂;у₂;z₂) параллельны соответственно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы ̅ ∙ = 0 или x₁·x₂ + y₁·y₂+z₁·z₂

= 0.

Пример.

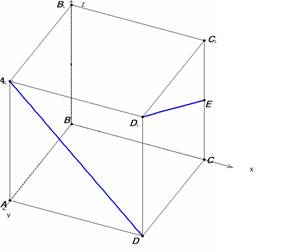
В кубе ABCDA₁B₁C₁D₁ найдите угол  между прямыми A₁D и D₁E , где Е – середина  ребра CC₁ .

Решение.

1-й способ.   

 Пусть F – середина ребра  ВВ₁ , а –ребро куба, φ - искомый угол.

Так как A₁ F ǁ D₁ E  , то φ - угол при вершине  A₁ в треугольнике A₁FD.

Из треугольника BFD имеем

FD² = BD² + BF² = 2a² + ^а = ^а ,

 а из треугольника A₁B₁F  получаем

а√

A₁F = .

                                                                                                    и                            .

2-й способ.

Введем прямоугольную систему координат, как указано на рисунке.

Не нарушая общности задачи, обозначим длину ребра куба а.

Тогда А₁(0; а; а), D(а; а; 0), D₁(а; а; а),

а

 Е(а; 0;  ).

Найдём координаты направляющих векторов прямых A₁D и D₁E  = {а; 0; −а},  = 0; −а; − ^а .

Тогда 

а·                ·( а)         ( а)·( ^а ) ^а сosφ =                       .

   и  .

Ответ:  arccos .

2) Задача на нахождение угла между прямой и плоскостью. 

•   Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.   0˚ < (a;α ) < 90˚ .

•   Угол между взаимно перпендикулярными прямой и плоскостью равен 90˚ .

•   Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0˚ .

   Угол между прямой l и плоскостью α можно вычислить:

1)   если этот угол удается включить в прямоугольный треугольник в качестве одного из острых углов;

| ∙ ̅|

2)   по формуле  sinφ =    или в координатной

                                                                                                                                                              |  |·| ̅|

форме

                                                                                                                            |    ∙            ∙            ∙   |

  , где

(x₁ ; y₁ ; z₁) - вектор нормали плоскости α ,

̅(x₂ ; y₂ ; z₂) - направляющий вектор прямой l;

•   прямая l и плоскость α параллельны тогда и

только тогда, когда   x₁ x₂ + y₁ y₂ + z₁ z₂ = 0 .

Пример.

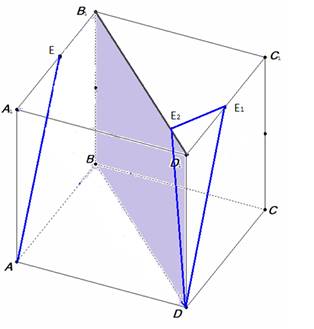
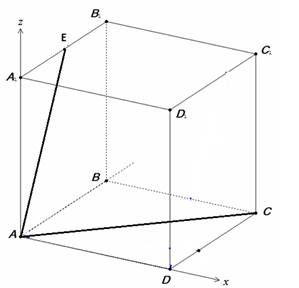
В кубе ABCDA₁ B₁ C₁ D₁ точка Е – середина ребра  A₁ В₁ . Найдите синус угла между прямой АЕ и плоскостью  ВDD₁ .

Решение.

1-й способ.

     Угол между прямой АЕ и плоскостью ВDD₁ будем искать как угол  между данной плоскостью и прямой DЕ₁, параллельной прямой АЕ.

Из точки Е₁ опустим перпендикуляр Е₁Е₂ на прямую В₁D₁.

Искомый угол – это угол между прямыми DE₂ и DE₁. Пусть сторона куба равна а. 

А.

Е₁Е₂ .

DE₁ =   а       =         .

                                    √       а√              √

.

Ответ: .

2-й способ. 

Введем прямоугольную систему координат, как указано на рисунке.

Не нарушая общности задачи, обозначим длину ребра куба а.

За вектор нормали плоскости ВDD₁ возьмем вектор         .

Найдём координаты нужных точек.

а

А(0; 0; 0), Е(0;  ; а), С(а; а; 0).

Тогда           = 0; ^а ; а ,         = {а; а; 0}.

                                  ^а·а а·                             √

.

Ответ: .

3)  Задача на нахождение угла между двумя плоскостями.

•   Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.

•   Величина двугранного угла принадлежит промежутку (0˚ ;180˚ ).

•   Величина угла между пересекающимися плоскостями принадлежит промежутку (0˚

;90˚ ].

•   Угол между двумя параллельными плоскостями считается равным 0˚ . Угол между пересекающимися плоскостями можно вычислить:

1)   как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения;

2)   как угол треугольника, если удается включить линейный угол в некоторый треугольник;

3)   как угол между перпендикулярными им прямыми;

4)   по формуле  

  cos ∠(α; β) = ^{| ∙ |}  или в координатной форме | | ∙ | |

|АА + ВВ + СС |

cos ∠(α; β) = ,   

                                                                                                                                                                                                                                                  А    + В    + С    ∙    А    + В    + С

                                                                                                 где                                            (                         А ; В ; С ) −

                                                                                                   вектор нормали плоскости           +           +         +

= 0,

                     (А ; В ; С ) − вектор нормали плоскости               +           +          +        = 0. 

Пример.

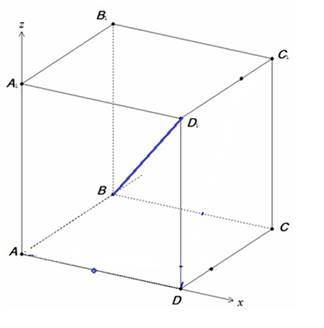
Основание прямой четырехугольной призмы ABCDA₁B₁C₁D₁ - прямоугольник ABCD, в котором АВ = 12, AD  . Найдите косинус угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой 

BD₁, если расстояние между прямыми AC и  B₁D₁ равно 5.

Решение.

 1-й способ.

    Решение этой задачи вычислительноаналитическим методом очень громоздкое и сложное, даже выполнить чертеж к этой задаче крайне сложно, поэтому я его не привела, а методом координат эта задача решается легко и просто.  

2-й способ.

   Легко видеть, что этот угол равен углу между нормалями к этим плоскостям.

 Вектор          – вектор нормали плоскости основания.

А вектором нормали плоскости, проходящей через середину ребра АD перпендикулярно прямой ВD₁ будет вектор           .

   Введем прямоугольную систему координат, как указано на рисунке.

Найдём координаты нужных точек, т.е. точек А, А₁, В, D₁.

А (0; 0; 0), А₁(0; 0; 5), В(0; 12; 0),

 D; 0; 5).

Тогда              = {0; 0; 5},            .

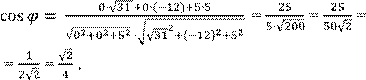
Ответ:  .                                     

     Прорешав множество задач типа 14 из литературы, для подготовки к Единому Государственному Экзамену, я выяснила, что стереометрические задачи на нахождение углов в пространстве можно разделить  на три группы:

1)   это задачи на нахождение угла между скрещивающимися прямыми, 

2)   задачи на нахождение угла между прямой и плоскостью и  3)   на нахождение угла между двумя плоскостями. 

    Так как, я считаю, что векторно-координатный метод является более рациональным, то я сформулировала алгоритмы решения стереометрических задач данным методом по озвученной теме. 

     Алгоритм нахождения угла между скрещивающимися прямыми: 

1)   мы ввели прямоугольную систему координат,

2)   нашли координаты нужных точек, 

3)   затем нашли координаты направляющих векторов прямых и  4) вычислили косинус угла между ними. 

     Следующий алгоритм несущественно отличается от предыдущего. 

Алгоритм нахождения угла между прямой и плоскостью.

Третьим шагом мы должны ввести нормальный вектор к плоскости и найти его координаты, а затем вычислить синус искомого угла. Он равен косинусу угла между направляющим вектором прямой и вектором нормали  к плоскости. 

     При решении задачи на нахождение угла между двумя плоскостями, необходимо найти координаты нормальных векторов к заданным плоскостям и вычислить по формуле модуль косинуса угла между этими векторами.

    Таким образом, я определила виды стереометрических задач на нахождение углов в пространстве, включённых в ЕГЭ. Выявила и освоила более рациональный метод их решения.

Список использованной литературы: 

1.      А.С., Пантелеев А.В., 2005 (электронное приложение).

2.      Бунеева Н.А, Каргаполов А.М. Задачи по стереометрии (координатный метод), 2006. Высшая математика в упражнениях и задачах в 2-х частях. Данко П.Е., Попов А.Г., Кожевников Т.Я. Год выпуска: 1986.

3.      Газета «Математика» №8, 2016 г, издательский дом «Первое сентября».

4.      Математика ЕГЭ – 2018, задания 14, Корянов А.Г., г Брянск.

5.      Семенов А.Л, Ященко И.В. ЕГЭ – 2017. Типовые тестовые задания, МИОО,

«Экзамен», 2018

6.      Высшая математика, Учебник для ВУЗов, Шипачев В.С., 1998. Глава 3.

Аналитическая геометрия на плоскости 34 4. Угол между двумя прямыми Глава 9. Аналитическая геометрия в пространстве 222 (46) § 11. Уравнения плоскости 244

1. Общее уравнение плоскости (244). 2. Угол между двумя плоскостями (245).

Нормальное уравнение плоскости. Расстояние от точки до плоскости (246).

7.      Единый Государственный экзамен: математика: методика подгот.: кн. для учителя / [Л.О.Денищева, Ю.А.Глазков, К.А. Красньянская и др.]. – М.:

Просвещение, 2005. – 256 с.

8.      История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.Том 3 Математика XVIII столетия. (1972) Краткий курс высшей алгебры. Дураков Б.К. Год выпуска: 2006.

9.      Краткий курс высшей алгебры. Дураков Б.К. Год выпуска: 2006.

10. Ларин А.А. Электронный учебник "Курс высшей математики": Часть1 11. Саррюс, Фредерик-Пьер // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

12.   htt :// www . webmath . ru –открытый банк заданий ЕГ Э

13.   http://www.fipi.ru

14.   alexlarin.net

15.   ege.sdamgia.ru