
Сумма и разность синусов и косинусов.
(Формулы преобразования сумм в произведение).
I. Вывод формул:
1. sin α + Sin β = …
2. sin α - Sin β = …
3. cos α + cos β = …
4. cos α - cos β = …
II. Записать выведенные формулы в тетрадь.
III. Решение примеров на полученные формулы.
Пример 1. Вычислить sin 75° + sin 15°.
Решение.
Воспользуемся формулой суммы синусов (№1)
sin
75° + sin 15°= 2sin ![]() ˔ cos
˔ cos ![]() = 2˔sin
45°˔ cos 30°=
= 2˔sin
45°˔ cos 30°=
2˔![]() ˔
˔![]() =
= ![]() . Ответ:
. Ответ:![]()
Пример 2. Упростить
и вычислить выражение при α =![]()
![]() ( sin
4α - sin
2α ).
( sin
4α - sin
2α ).
Решение.
Воспользуемся формулой разности синусов (№2).
![]() ( sin
4α - sin
2α )=
( sin
4α - sin
2α )= ![]() ˔ 2˔ sin
α˔cos
3α =
˔ 2˔ sin
α˔cos
3α =![]() ˔ 2˔
˔ 2˔![]() ˔0 =0
˔0 =0
Ответ:![]()
Пример 3. Упростить и вычислить выражение:
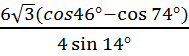 .
.
Решение.
Воспользуемся формулой разности косинусов (№4).
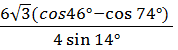 =
= 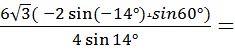
![]()
![]() = 4,5
= 4,5
Ответ:![]()
Пример 4.
Преобразовать в произведение: 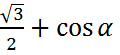 .
.
Решение.
Сделаем замену ![]() = cos
30° и
воспользуемся формулой суммы косинусов (№3).
= cos
30° и
воспользуемся формулой суммы косинусов (№3).
cos
30° +![]() = 2 cos
= 2 cos![]() cos
cos![]() =
=
2 cos
(15°+![]()
Пример 5. Упростить
и вычислить выражение при α =![]()
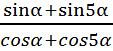 .
.
Решение.
Воспользуемся формулами суммы синусов и суммы косинусов (№1 и №3).
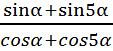 =
=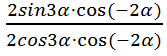 =
= 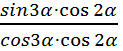 =tg3α
=tg3α
tg
3˔![]() =
tg
=
tg ![]() = 1.
= 1.
Ответ:![]()
Домашняя самостоятельная работа.
Вычислить:
1. cos 105° + cos 75°
2. sin 105° - sin 75°
3. cos
![]() + cos
+ cos ![]()
4. cos
![]() - cos
- cos ![]()
Преобразовать в произведение:
5. 1 - sin x
6. 1 + 2sin x
7. 1+ 2 cos x
8. 1 – cos x
9. Упростить
и вычислить выражение при α =![]()
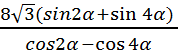 .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.