Свойства и график функции у = cosх

Филиал бюджетного профессионального образовательного учреждения Чувашской Республики

«Чебоксарский медицинский колледж»

Министерства здравоохранения Чувашской Республики в городе Канаш

Свойства и график функции  y = cos x

специальность 34.02.01 Сестринское дело (базовая подготовка)

учебная дисциплина БД.04 Математика

Канаш, 2020

Л1. Сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;

Л2. Понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;

Л8. Отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;

• метапредметных:

М1. Умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

М5. Владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

М7. Целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;

• предметных:

П1. Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;

П2. Сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

П5. Сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №3. Свойства и график функции y=cos x

Перечень вопросов, рассматриваемых в теме

·         Изучение свойств функции ;

·         Построение графика функции;

·         Расположение промежутков монотонности функции ;

·         Определение свойств и положения графика тригонометрических функций вида  и ;

·         демонстрирование уверенного владения свойствами функции ;

·         объяснение зависимости свойств и положения графика функции вида  и ,от значения коэффициентов a, k, b.

Глоссарий по теме

Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении.

Функция y=f(x) возрастает на интервале X, если для любых  и ,  выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X, если для любых  и ,  выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.

Точку х₀  называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают y_max.

Точку х₀  называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают y_min.

Основная литература:

Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Напомним, что все тригонометрические функции являются периодическими функциями. Функции  и  повторяются через каждые 360° (или 2π радиан), поэтому 360° называется периодом этих функций (рис.1).

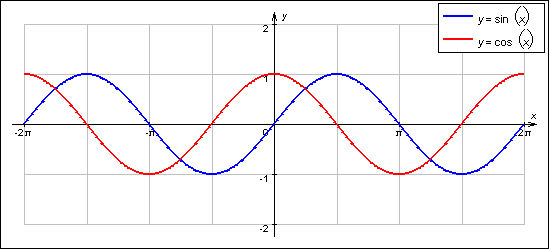
Рис. 1 – графики функций  и .

Функции  и  повторяются через каждые 180° (или π радиан), поэтому 180° — это период для данных функций (рис. 2).

Рис. 2 – графики функций  и .

В общем случае если  и  (где  — константа), то период функции равен  (или  радиан). Следовательно, если , то период этой функции равен , если , то период этой функции равен .

Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1).

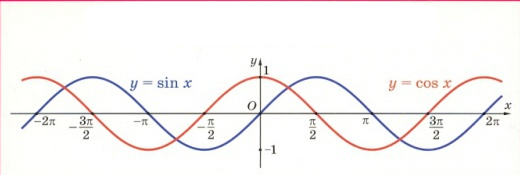
Рис. 3 – изображение амплитуды графиков  и .

Однако, если , каждая из величин  умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для  амплитуда равна 5, а период — .

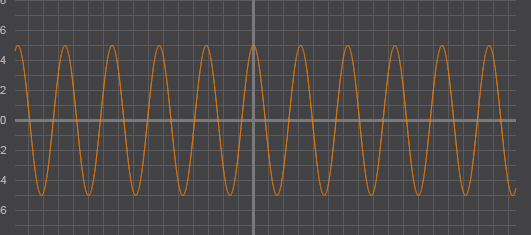
Рис. 4 – график функции .

Свойства функции :

1. Область определения - множество R всех действительных чисел.
2. Множество значений - отрезок [−1;1].
3. Функция  периодическая, Т=2π. 
4. Функция  - чётная
5. Функция  принимает:

·         значение, равное 0, при 

·         наибольшее значение, равное 1, при 

·         наименьшее значение, равное −1, при ;

·         положительные значения на интервале  и на интервалах, получаемых сдвигами этого интервала на ;

·         отрицательные значения на интервале  и на интервалах, получаемых сдвигами этого интервала на .

1. Функция 

·         возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на ;

·         убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на .

Интересно, что графиками тригонометрических функций –косинус и синус описываются многие процессы в нашей жизни. Например, работа сердца. Сделанная электрокардиограмма (ЭКГ) представляет собой график синусоиды, отражающую биоэлектрическую активность сердца. Или еще пример, электромагнитные волны к ним относятся: мобильные телефоны, беспроводная связь, радио, СВЧ-печи тоже распространяются по закону синуса или косинуса. Их существование было предсказано  английским физиком Дж.Максвеллом в 1864 году.

Актуализация знаний

Напомним, что множество значений функции y=cosx принадлежит отрезку [–1;1], определена данная функция на всей числовой прямой и, следовательно, функция ограничена и график её расположен в полосе между прямыми y=–1 и y=1.

Так как функция периодическая с периодом , то достаточно построить её график на каком-нибудь промежутке длиной , например на отрезке  Тогда на промежутках, полученных сдвигами выбранного отрезка на , график будет таким же.

Функция  является чётной. Поэтому её график симметричен относительно оси Оу. Для построения графика на отрезке  достаточно построить для а затем симметрично отразить его относительно оси Оу (рис. 5)

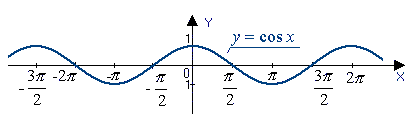
Рис. 5 – график функции .

Примеры и разборы решения заданий тренировочного модуля:

Пример 1. Найдем все корни уравнения  , принадлежащие отрезку .

Построим графики функций  и  (рис. 6)

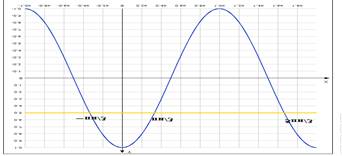
Рис. 6 – графики функций  и .

Графики пересекаются в трёх точках, абсциссы которых  являются корнями уравнения . На отрезке от  корнем уравнения является число . Из рисунка видно, что точки х₁ и х₂ симметричны относительно оси Оу, следовательно . А .

Пример 2.Найти все решения неравенства  , принадлежащие отрезку .

Из рисунка 6 видно, что график функции  лежит ниже графика функции  на промежутках  и 

Ответ: , .

VIII. Подведение итогов уроков

Скачано с www.znanio.ru