Свойства целочисленных операций с mod N.docx

Свойства целочисленных операций с mod N

Любые целые числа сравниваются по модулю N отображением их на множество модуля N

равное {0, 1, 2,…. N – 1}                                                (1)

Для неотрицательных чисел а ³ 0 отображение их на множество модуля получается циклическим вычитанием из ‘a’ величины N до тех пор пока не получится результат r, принадлежащий множеству модуля. Этот результат и есть число ‘a’ представленное (взятое) по модулю N

r = a mod N                                                (2)

Если a < N, то r = a. Произошло отображение ‘a’ на самое себя.

Для отрицательных целых чисел a < 0 отображение на множество модуля распространяется путем циклического прибавления N к а.

Операции сравнения по модулю N наглядно можно представить на оси целых чисел, см. рисунок ниже, как счет пачками по N единиц направленный от заданного числа в сторону множества модуля N.

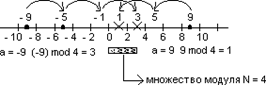Рисунок 3.1

Легко видеть, что для неотрицательных чисел величина r есть остаток от целочисленного делителя ‘a’ на N.

В языке Pascal есть операция mod – целый остаток от деления двух целых положи тельных чисел.

Понятия a mod (-N) не существует, а взять отрицательное целое по модулю N можно так:

— 9 mod 4 =- (9 mod 4)= — 1 + 4 = 3                                                   (3)

Можно и воспользоваться функцией Int(x) – целое число

Для а > 0 r = a mod N = a – N * Int(a/N)                                      (4)

Для a < 0 r = a mod N = a + N * (Int(-a/N)+1)

Например:

r = 9 mod 4 = 9 – 4 * Int(9/4) = 9 – 4*2 = 9 – 8 = 1

r = –9 mod 4 = –9 + 4 * (Int(+9/4) = — 9 + 4*(2+1) = 3

В теории чисел определено отношение (º) сравнимости целых чисел: a º b (mod N)                                                           (5)

‘a’ сравнимо с ‘b‘ по модулю N, ‘a‘ и ‘b‘ – целые, N ¹ 0, если только выполняется равенство a = b + k*N

Еще говорят: N делит (a –b): N| (a-b) и ‘b’ называют вычетом числа ‘a' по модулю N.

Выражение (5) равносильно утверждению, что остатки от делений ‘a‘ и ‘b’ на N равны

17 º 5 (mod 12) означает, что 17 mod 12 = 5

5 mod 12 = 5

Для N = 12 полный набор вычетов есть {0, 1, 2, … 11}

Выражение a º 1 (mod N) определяет все целые положительные ‘a’, остатки от деления которых на N равны 1.