
Степаненкова Нина Павловна, учитель математики, высшая квалификационная категория, муниципальное общеобразовательное учреждение «Средняя школа с углубленным изучением отдельных предметов №81 Центрального района Волгограда»
Технологическая карта урока по геометрии «Признаки равенства прямоугольных треугольников в задачах», 7 класс
«Если Вы хотите участвовать в большой жизни,
то наполняйте свою голову математикой».
М.И. Калинин.
|
Тема урока |
Признаки равенства прямоугольных треугольников в задачах. |
|
Дидактические цели урока |
· Создать условия для осознания и осмысления блока учебной информации (четыре признака равенства прямоугольных треугольников),применяя знания в знакомой и новой учебных ситуациях. · Проверить уровень усвоения системы знаний и умений по данной теме. |
|
Идея урока |
· Развивать наблюдательность, умение сравнивать, анализировать, делать выводы. · Показать использование учебных знаний в жизненных ситуациях на задачах с практическим применением. |
|
Теоретическая составляющая урока (перечень понятий и их свойств) |
· Треугольник, его элементы · Прямоугольный треугольник, его свойства. · Равнобедренный треугольник, его свойства. · Признаки равенства треугольников. · Признаки равенства прямоугольных треугольников. · Расстояние от точки до прямой. |
|
Практическая составляющая урока (список систем задач, которые должны быть решены в ходе урока; их целевое назначение, а также приемы или методы их конструирования, особенности задач) |
Приложение №1 |
|
Мотивация (приемы организации на каждом этапе урока) |
1. Устная фронтальная работа по готовым рисункам (наблюдают, сопоставляют, анализируют). 2. Работа в группах с последующим выступлением представителей (участвуют в коллективном обсуждении, строят рассуждения, презентуют свои решения, развивая и совершенствуя свою речь для регулирования действий). 3. Учебный диалог (осознание и осмысление учебной информации и применение ее к жизненной ситуации, переформатирование информации от текстовой к математической схеме). 4. Самостоятельная работа (проверка уровня усвоения знаний). 5. Частично- поисковая работа (выбор и применение уже полученных знаний, осмысление новых знаний) 6. Работа в группах (синквейн – креативность, отбор и осмысление главного, творчество, ассоциативность). |
|
Актуализация знаний (особенности организации) |
1. Устная фронтальная работа по готовым рисункам, изображенным на слайде, на узнавание признаков равенства треугольников. 2. Работа в группах с последующим выступлением представителей. 3. Устная фронтальная работа по готовым рисункам, изображенным на слайде, на нахождение невозможного. 4. Учебный диалог (работа вместе с учащимся у доски). 5. Самостоятельная работа по вариантам. 6. Частично- поисковая индивидуальная работа, с поэтапной проверкой на слайдах и вербальной фиксацией затруднений в деятельности учащихся. 7. Работа в группах. Рефлексия (синквейн). |
|
Основная часть урока (этапы используемых методик) |
· Смотрю, вижу («Микрофон»); · Работа в группах, выступления их представителей; · Смотрю, вижу («Лови ошибку»); · Учебный диалог(коллективная беседа); · Самостоятельная работа (по вариантам); · Включение нового в систему знаний (частично – поисковый). |
|
Рефлексия деятельности учащихся (как определялась результативность деятельности учащихся) |
Синквейн. Пример одного, из полученных на уроке. Треугольники Произвольные Прямоугольные Выбираем, сравниваем, доказываем. «Чтобы переварить знания, надо поглощать их с аппетитом» Геометрия в картинках! |
|
Итог урока (особенности организации) |
1. Оценки за работу на уроке (работая устно,ученики получали «бонусы», по их количеству оценивается работа на уроке, работа у доски, оценки за с/р узнают на следующем уроке). 2. Д/з 3. Притча: «Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?» и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!» (общая оценка учителем работы класса в соответствии со словами притчи) |
|
Технические ресурсы урока (как именно ИКТ были использованы,для чего и на каком этапе) |
ПК, проектор. Изображение при решении задач на применение доказанных утверждений. Поэтапное изображение при решении задачи на доказательство признака равенства треугольников по стороне и высотам, проведенным к другим сторонам. |
Приложение №1.
Практическая составляющая урока
(список систем задач, которые должны быть решены в ходе урока; их целевое назначение, а также приемы или методы их конструирования, особенности задач).
1. Задачи на применение доказанных утверждений.
· На рисунке найти равные треугольники. Объяснить.
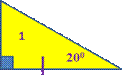
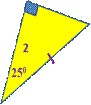

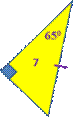




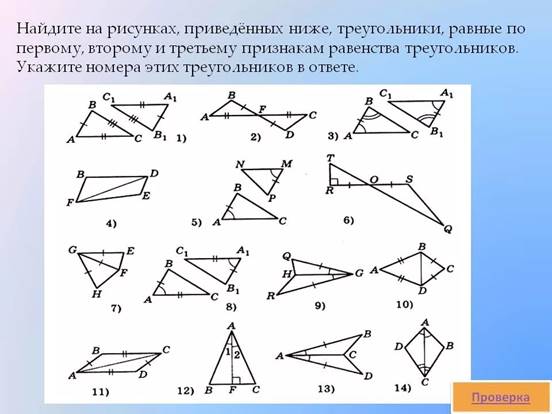
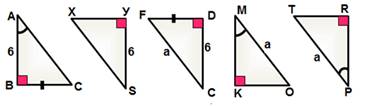
· Работа в группах.
По готовым чертежам доказать равенство треугольников.
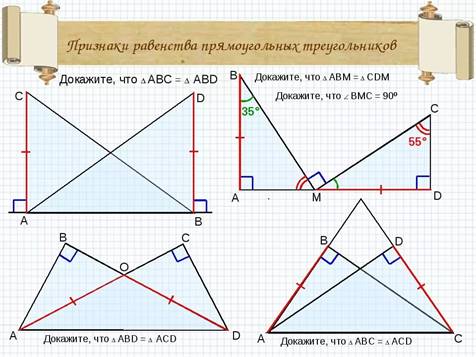
· Найти невозможное. Объяснить.
На рисунке представлены различные треугольники. Среди них есть треугольники с двумя прямыми углами, равносторонний прямоугольный треугольник, прямоугольный,сумма острых углов которого больше или меньше 90 градусов, треугольник с известными сторонами, где гипотенуза меньше катета, прямоугольный треугольник с углом 30 градусов, но правило противолежащего катета не выполняется.
2. Задачи с практическим содержанием.
Задача 1
Двое учащихся вышли из школы. Один прошел 200 м на запад и 300 м на север. Второй прошел 300 м на восток и 200 м на юг. Кто из учащихся оказался дальше от школы?
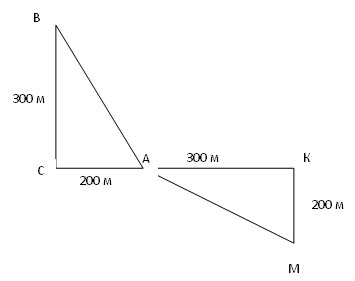
Задача 2
Смоленск и Брянск находятся примерно на расстоянии 395 км от Москвы. Где между Смоленском и Брянском надо поставить автозаправку Х, чтобы расстояние от нее до Москвы было наименьшим?
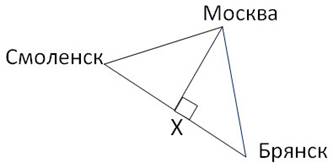
Задача 3.
Столяру нужно заделать отверстие треугольной формы. Сколько размеров и какие он должен снять, чтобы изготовить латку?
Что он должен измерить, если отверстие имеет форму
а) прямоугольного треугольника;
б) равностороннего треугольника;
в) равнобедренного треугольника.
Самостоятельная работа (по вариантам)
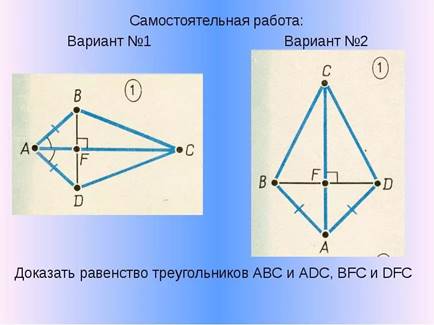
4. Задачи на доказательство новых утверждений с опорой на ранее изученное.
Задача 1
Доказать, что любая точка биссектрисы угла равноудалена от его сторон.
Задача 2
Верно ли, что треугольники равны, если в них есть пара равных сторон и, также равны высоты, проведенные к двум другим сторонам?
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.