Тема "Решение задач на проценты"

Урок алгебры в 9 классе

Разработала и провела: Сигида Ю.А.

Тема: Сложные проценты. Решение задач на проценты.

Цели урока: ознакомить учащихся с понятием сложных процентов, формировать умения решать задачи на проценты с помощью формул «сложных процентов», в том числе повышенной сложности, повторить методы решения задач на проценты; научить переводить реальные ситуации в математические модели задач;

Развивать критическое мышление, функциональную математическую грамотность, умение работать в группах, анализировать и делать выводы.

Воспитывать культуру речи, умение принимать оптимальные решения при решении жизненных задач, привитие любви к процессу обучения, к стремлению получения новых знаний.

Тип урока: урок изучения нового материала, применения новых и прежних знаний, умений.

Оборудование: презентация к теме «Сложные проценты», интерактивная доска, раздаточный материал.

Ход урока.

1.     Организационный момент.

Приветствие и краткое введение в тему урока.

«Черный ящик» (Что спрятано в ящике?)

1.     Я часть целого, но не могу быть меньше нуля. Что я такое?

2.      Я в жизни очень важен, и в магазине все меня знают, частенько нужен в бизнесе, я окружаю вас буквально повсюду.

3.     Скидки или акции – я тут как тут. Я могу показать сколько ты сэкономишь или сколько потеряешь. Я финансах важен, без меня никуда.

Это конечно же «процент». На уроке с вами разберём тему Сложных процентов, познакомимся с понятием и формулами сложных процентов, будем решать задачи с использованием формул «сложных процентов», развивать математическую речь и функциональную грамотность (учение применять теоретические знания)

И я вам желаю на уроке:

Не просто слушать, а слышать

Не просто смотреть, а видеть

Не просто отвечать, а мыслить

Дружно и слажено работать.

2.     Устная работа.

1.     Что называют процентом?  (Процентом называется одна сотая часть какого-либо числа)

2.     Как обозначается 1%?  (1%? = 0,01)

3.     Как перевести десятичную дробь в проценты? (умножить на 100).

4.     А как перевести проценты в десятичную дробь? (разделить на сто, т.е. умножить на 0,01)

5.     Представьте данные десятичные дроби в процентах: 0, 54; 1,26; 0,8; 23, 27

6.     Представьте проценты десятичными дробями: 34%, 120%; 5%; 54,7%

7.     Найдите 15% от 400 (60)

10% от 5500 (550)

25% от 3000 (750)

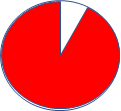
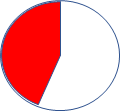
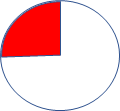
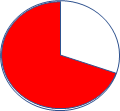
1)                                              2)                                                  3)                                              4)

Найдите пару:

А) 25%                  Б) 15%                         В) 70%                    Г) 40%          Д) 50%

3.     Формирование новых знаний и навыков.

Знания о процентах необходимы не только для решения математических задач, но и имеют важную роль в практическом применении при решении жизненных задач. Без процентов не обойтись экономистам, бухгалтерам, работникам финансовых учрежденийи  практически каждый день необходимо решать задачи с использованиепм процентов. Сегодня мы с вами побудем немножко работниками банка и будем решать задачи для начисления процентных денег.

Давайте рассмотрим некоторые банковские термины: «банковский процент» - плата за пользование заёмными денежными средствами, депозит – сумма денег, которую клиент вносит на хранение в банк, «кредит» - экономические отношения, при которых одна сторона получает от другой денежные средства, товары.

Скажите мне как вы представляете понятие «сложные проценты». Давайте попробуем сформулировать, о чем сейчас пойдёт речь. (ответы учеников) 

При применении простых процентов доход рассчитывается от первоначальной суммы вложенных средств не зависимо от срока вложения. В финансовых операциях простые проценты используются преимущественно при краткосрочных финансовых сделках.

При применении сложных процентов накопленная сумма процентов добавляется во вклад по окончании очередного периода начислений. При этом каждый раз её изменение составляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе. В этом случае имеем дело со «сложными процентами» (т.е. начисляется процент на проценты).

Давайте посмотрим будет ли различие между начислениями применяя простые или сложные проценты.

 Так, если банковская ставка равна 30%, а первоначальная сумма 50000 руб., то накопленная сумма за три года при применении простых и сложных процентов будет иметь вид:

Таблица 1. Накопленная сумма с использованием простых и сложных процентов.

Формулы простых и сложных процентов.

A_n = А₀ (1 ±  )ⁿ – формула сложных процентов, где знак «+» или «-» ставятся в соответствии с тем, к чему приводит «прирост» - к увеличению или уменьшению величины.

4.     Закрепление теоретических знаний на практике. Решение задач

Задача 1. (Решение у доски)

В банке открыт срочный депозит на сумму 50000 под 15% на 3 года. Рассчитать накопленную сумму если проценты:

а) простые; б) сложные.

Работа в парах (группах)

Задача (1 группа).

Вкдадчик внес в банк 4000 рублей под 20% годовых. Сколько рублей он получит прибыли через 4 года?

Вкдадчик внес в банк 10000 рублей под 25% годовых. Сколько рублей он получит прибыли через 3 года?

Задача (2 группа)                       

Один из видов срочных вкладов предусматривает начисление 9% прибыли через год хранения денег в банке. Если спустя этот срок счет не закрывается, то договор автоматически продлевается на тех же условиях (пролонгируется). Какая сумма будет на счету через 3 года при первоначальном вкладе 17 000 рублей и при той же процентной ставке? Результат (в рублях) округлите до целых.

Решение. По условию задачи А₀ = 17 000, p = 9, n = 3, тогда искомая величина равна A₃ = 17 000 · (1 + 9\100 )³ = 22 015,493≈22 016 (руб.).

Ответ: 22 015,5 рублей.

Задача (3 группа).

Известно, что ставка банковского процента равна 25%. Определит, через сколько лет начальный вклад 216 000 рублей возрастёт до 421 875 рублей.

Задача (4 группа).

Цена ноутбуков, не проданных в текущем году, уменьшалась каждый последующий год на одно и то же число процентов от предыдущей цены. На сколько процентов каждый год уменьшалась цена ноутбука, если выставленный на продажу за 40000 рублей, он через да года был продан за 23104 рубля.

Гений – это 1% таланта и 99% труда (Томас Эдисон)   

5.     Подведение итогов. Рефлексия:

• - С какими новыми понятиями мы познакомились на уроке?

• - Что такое "сложный процент"?  Чем он отличается от «простого процента»?

•  - Как найти "сложный процент"? 

• - Где используется эти проценты?

6.     Домашнее задание:

Задача 2 (у доски)

В банке открыт срочный депозит на сумму 20000 рублей под 20%. Рассчитайте накопленную сумму на 3 года если проценты простые

Задача 3 (у доски)

В банке открыт срочный депозит на сумму 4000 рублей под 20%. Рассчитайте накопленную сумму на 2 года, если проценты сложные

Группа 1

Если банковская ставка равна 30%, а первоначальная сумма 50000 руб., то накопленная сумма за два года при применении простых и сложных процентов будет иметь вид:

Группа 2

Если банковская ставка равна 30%, а первоначальная сумма 50000 руб., то накопленная сумма за три года при применении простых и сложных процентов будет иметь вид:

Группа 3

Если банковская ставка равна 30%, а первоначальная сумма 50000 руб., то накопленная сумма за первый год при применении простых и сложных процентов будет иметь вид: