Тема урока «Решение задач по теме: Гармонические колебания».

.09.Цели урока:

а)  образовательная:  проверить  усвоение  физических  формул  и  умений    брать  первую  и

вторую  производную  от  тригонометрических  функций,  формировать  умения  решать

расчетные и качественные задачи, анализировать графики и физические закономерности.

б)  развивающая:  развивать  творческое  мышление,  развивать  умение  применять  знания  в

новой  нестандартной ситуации, развивать умение анализировать, делать выводы.

в)  воспитательная:  воспитывать  доброжелательное  отношение  друг  к  другу,

взаимопонимание и взаимопомощь. 

09.11.2021г.     11 класс

Тема урока «Решение задач по теме: Гармонические колебания».

Цели урока:

образовательная: проверить  усвоение  физических  формул  и  умений    брать  первую  и

вторую  производную  от  тригонометрических  функций,  формировать  умения  решать

расчетные и качественные задачи, анализировать графики и физические закономерности.

развивающая: развивать  творческое  мышление,  развивать  умение  применять  знания  в

новой  нестандартной ситуации, развивать умение анализировать, делать выводы.

воспитательная: воспитывать  доброжелательное  отношение  друг  к  другу,

взаимопонимание и взаимопомощь. 

Выполнила: Керимова Ирина С.

                                                          Ход урока:

       I.            Организационный момент урока.

    II.            Организация внимания учащихся.

Тема нашего урока: Решение задач «Гармонические колебания».                                    Сегодня мы вспомним понятия периода, частоты, амплитуды колебаний и научимся применять эти понятия  при решении задач.

 III.            Повторение пройденного материала

1)      Прежде чем перейти к решению задач, предлагаю проверить как вы к этому готовы.

Решить кроссворд

 IV.            Решение задач.

1)      Алгоритм решения задач (есть у каждого)

1.      Внимательно прочитать условие задачи и увидеть мысленным взором конкретную  ситуацию, представленную в задаче.

2.      Записать кратко  условие задачи, перейти, если необходимо в систему СИ.

3.      (А вот теперь!) Проанализировать условие задачи на предмет, что известно в задаче и что надо найти.

4.      Составить систему уравнений и решить ее относительно неизвестных.

5.      Вывести размерность в полученных формулах, сделать расчет ответов.

6.      Проанализировать ответы (эта часть решения задачи хоть и заключительная, но не самая легкая: необходимо рассмотреть, для каких случаев работает полученная формула, когда ответ не имеет физического смысла и реален ли полученный численный ответ).                                            

2)      Работа с текстом.

А.    Рассмотрите график и заполните пропущенные записи в тексте.    

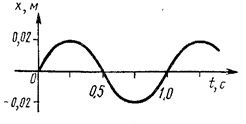График колебания: t – время в секундах;  X –смещение в метрах.                          

По графику колебаний  определяют амплитуду смещения и период

(Х _м = 0,02 м = 2см;     Т= 1 с).                                                  

Частоту колебаний   рассчитывают по формуле:   (v =;   v =  = 1 Гц)  (1 колебание за 1 секунду).

Б.      По графикам определить амплитуду смещения, период. Рассчитать по формуле частоту. Решение оформить следующим образом, графики не рисовать:

3)      Задачи

1.       Напишите уравнение гармонических колебаний, если частота равна 0,5 Гц, амплитуда 80 см. Начальная фаза колебаний равна нулю.

Решение: 

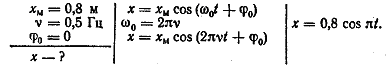
2.      Напишите уравнение гармонических колебаний, если амплитуда равна 7 см и за 2 мин совершается 240 колебаний. Начальная фаза колебаний равна π /2 рад.

Решение: 

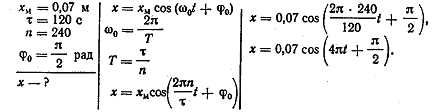
3.      Ай да Фуко (данная презентация готовится учащимся класса)

- Как использовался математический маятник для доказательства вращения Земли?

           Одно из самых наглядных доказательств было найдено французским физиком Фуко.  В  1850  году  он  подвесил  огромный маятник  в  парижском  Пантеоне-зале  с  очень  высоким  куполом. Длина подвеса была равна 67 м. Масса шара 28 кг. Маятник качался несколько часов подряд. Снизу шар имел острие, а на полу насыпали кольцом  грядочку  из  песка.  Маятник раскачивали.  Острие  стало оставлять  на  песке  бороздки.  Через  несколько  часов  он  чертил бороздки  в  другой  части  грядочки.  Плоскость  колебаний  маятника словно поворачивалась по часовой стрелке. На самом деле плоскость

колебаний маятника сохранялась.  Вращалась  планета,  увлекая  за собой  Пантеон  с  его  куполом  и  песочной  грядкой  (на  экране  фото маятника Фуко).

- Был ли в России повторен опыт Фуко?

Опыт Фуко был повторен в Исаакиевском соборе в Петербурге.

Маятник совершал    3 колебания за минуту.  Исходя  из  этих  данных

вы можете оценить длину маятника, следовательно, и высоту

Исаакиевского собора.

4.      Первый маятник Фуко (1891, Париж) имел период колебаний 16 с. Определите длину маятника. Примите g =9,8 м/с².

Решение:          

Т=16с            

g=9,8м/с²           

                        l=

l -?

    V.            Домашнее задание

·         Повторить тему из математики «Производные функции»;

·         Р№ 429, 430

·         §§18-22

 VI.            Подведение итогов урока.

 Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.  На рисунке изображен график зависимости координаты от времени колеблющегося тела.

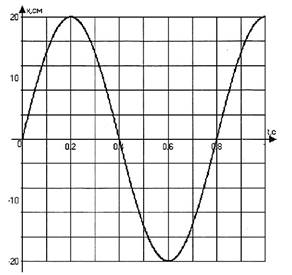
По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

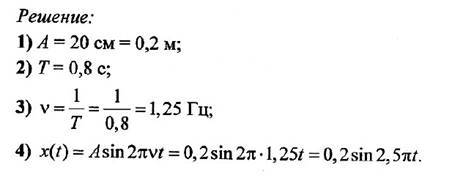
Цели урока:

а)  образовательная:  проверить  усвоение  физических  формул  и  умений    брать  первую  и

вторую  производную  от  тригонометрических  функций,  формировать  умения  решать

расчетные и качественные задачи, анализировать графики и физические закономерности.

б)  развивающая:  развивать  творческое  мышление,  развивать  умение  применять  знания  в

новой  нестандартной ситуации, развивать умение анализировать, делать выводы.

в)  воспитательная:  воспитывать  доброжелательное  отношение  друг  к  другу,

взаимопонимание и взаимопомощь. 

Скачано с www.znanio.ru