Тема урока: Производные высших порядков

Урок №  Тема урока: Определение дифференциала функции, его геометрический смысл.  Цели урока: 1. Обучающая: Рассмотреть определение дифференциала функции, его геометрический смысл.  2. Развивающая: способствовать развитию логического мышления, памяти.         3. Воспитательная: Аккуратное ведение конспектов, самодисциплина.    : Урок изучения нового материала          Тип  урока        Вид урока: лекция        Методы:  словесные                 Оборудование: раздаточный материал по теме урока. Ход урока.  I. Оргмомент II. Актуализация опорных знаний        Устный опрос  II. Целевая установка. 1. Тема урока                            2. Цель урока III. Формирование новых понятий и способов действий.  График дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства:   α где   – бесконечно малая в окрестности  функция. Для приближенного вычисления  значения функции f в точке x0 + Δx эту бесконечно малую функцию можно отбросить:  Линейную функцию  называют дифференциалом функции f в точке  x0  и обозначают   Поэтому пишут:  df. Для функции x производная в каждой точке  равна 1, то есть  Приближенное значение функции вблизи точки  x0 равно сумме ее значения в этой точке  и дифференциала в этой же точке. 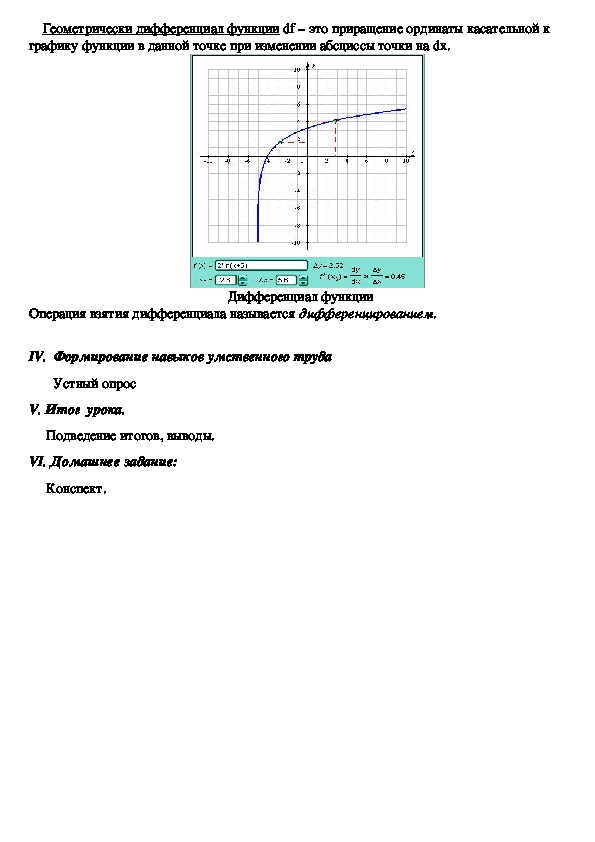Это дает возможность записать производную  следующим образом:  Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется  функция. Геометрически дифференциал функции df – это приращение ординаты касательной к  графику функции в данной точке при изменении абсциссы точки на dx. Операция взятия дифференциала называется дифференцированием. Дифференциал функции IV.  Формирование навыков умственного труда        Устный опрос    V. Итог  урока.       Подведение итогов, выводы. VI. Домашнее задание:          Конспект.