ТЕОРИЯ РЯДОВ. ОСНОВНЫЕ ПОНЯТИЯ В ИХ ИСТОРИЧЕСКОМ РАЗВИТИИ

Министерство образования и науки Российской Федерации федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Оренбургский государственный педагогический университет»

 

 

 

Физико-математический факультет

Кафедра математического анализа и методики преподавания математики

 

 

 

 

 

 

КУРСОВАЯ РАБОТА

ПО ДИСЦИАЛИНЕ МАТЕМАТИЧЕСКИЙ АНАЛИЗ

 

 

ТЕОРИЯ РЯДОВ. ОСНОВНЫЕ ПОНЯТИЯ В ИХ

ИСТОРИЧЕСКОМ РАЗВИТИИ

 

 

 

Направление подготовки:  44.03.01 Педагогическое образование

Профиль подготовки: Математика

Форма обучения: заочная

 

Выполнила студентка

Судакова Анастасия Андреевна

4 курс, 401-М группа

 

Научный руководитель:

Игнатушина Инесса Васильевна

                                                                       к.ф.-м.н., доцент

 

_________      ____________

                                                                                                                                         оценка                                  подпись

«        »                           20__ г.

 

 

 

Оренбург, 2015      

Содержание

 

Введение…………………………………………………..…………………….3

Глава 1. Общие положения теорем дифференциальных уравнений.

1.1 Основные понятия дифференциального уравнения……………………..5

1.2 Рекомендации к решению производственных задач с применением теории обыкновенных дифференциальных уравнений……………………………………7

Глава 2. Производственные задачи на составление обыкновенных

дифференциальных уравнений

2.1 задачи по физике…………………………………………………………...9

2.2 задачи по теоретической механике……………………………………....13

2.3 задачи по химии и технологии производства…………………………...18

2.4 задачи по экономике………………………………………………………21

Заключение. …………………………………………………………………....25

Список использованной литературы…………………………………………26

Приложения …………………..………………………………………………...28

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

Обыкновенные дифференциальные уравнения применяются для описания многих процессов реальной действительности. Трудно представить себе область науки или производства, в которой не возникала необходимость использования дифференциальных уравнений. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д.

Действительно, если некоторая физическая величина (перемещение тела, пластовое давление жидкости в фиксированной точке, концентрация вещества, объем продаж продукта) оказывается меняющейся со временем под воздействием тех или иных факторов, то, как правило, закон ее изменения по времени описывается именно дифференциальным уравнением, т.е. уравнением, связывающим исходную переменную как функцию времени и производные этой функции.

Независимой переменной в дифференциальных уравнениях может выступать не только время, но и другие физические величины: координата, цена продукта и т.д. Решение уравнения с анализом его зависимости от параметров задачи и начального состояния системы позволяет установить общие закономерности изменения исходной физической величины.

В этой связи изучение обыкновенных дифференциальных уравнений имеет теоретическое и прикладное значения. Дифференциальное уравнение является одним из основных математических понятий. Это – одна из наиболее сложных проблем, возникающих при изучении математического анализа. Важность и актуальность проблемы очевидна.

Объект исследования: обыкновенные дифференциальные уравнения.

Предмет исследования: применение обыкновенных дифференциальных уравнений к решению производственных задач.

Цель курсовой работы: рассмотреть производственные задачи, приводящие к обыкновенным дифференциальным уравнениям.

Задачи курсовой работы:

1) рассмотреть основные понятия, связанные с обыкновенными дифференциальными уравнениями.

2) подобрать производственные задачи, приводящие к обыкновенным дифференциальным уравнениям и дать рекомендации по их решению.

3) показать прикладной характер теории дифференциальных уравнений.

В данной работе приведены решения реальных практических задач, описываемых обыкновенными дифференциальными уравнениями.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Глава 1. Общие положения теории дифференциальных уравнений.

1.1. Основные понятия дифференциального уравнения

 

Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные( или дифференциалы) этой функции.

Если независимая переменная одна, то уравнение называется обыкновенным, если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных [1].

         ,     – дифференциальное уравнение, разрешенное относительно производной.

Уравнение вида ,        (*)

связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка [10].

     Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С1,С2,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С1, С2, …, Сn, обращающая вместе со своими производными у', у'',…, у(n) уравнение (*) в тождество.

     Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С1, С2, …, Сn определенные числовые значения [15].

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) обыкновенное дифференциальное уравнение первого порядка.

2) обыкновенное дифференциальное уравнение второго порядка.

3) обыкновенное дифференциальное уравнение третьего порядка

4) F общий вид обыкновенного дифференциального уравнения второго порядка.

5) уравнение в частных производных первого порядка [7].

Решением дифференциального уравнения называется такая дифференцируемая функция , которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.

Решением обыкновенного дифференциального уравнения в некотором промежутке  называют n раз непрерывно дифференцируемую в этом промежутке функцию x(t), удовлетворяющую при любом t  этому уравнению.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.2. Рекомендации к  решению производственных задач с применением теории обыкновенных дифференциальных уравнений

 

Обыкновенные дифференциальные уравнения являются моделями всевозможных процессов происходящих в физике, химии, биологии, теоретической механике и т.д. Решение задач на их составление ведет к осознанию связей между различными явлениями, происходящими в природе и обществе, к пониманию значения математики как прикладной науки [3].

Использование алгоритмического подхода способствует скорейшему и качественному освоению задач на составление дифференциальных уравнений.

Общего правила (алгоритма), которое позволяло бы, исходя из условий задачи, составлять и решать обыкновенные дифференциальные уравнения, не существует.

Обычно методика решения производственных задач с применением теории обыкновенных дифференциальных уравнений сводится к следующему:

1. Подробный разбор условия задачи и составление чертежа, поясняющего его суть.

2. Составление дифференциального уравнения рассматриваемого процесса.

3. Интегрирование составленного дифференциального уравнения и определение общего решения этого уравнения.

4. Определение частного решения задачи на основании данных начальных условий

5. Определение, по мере необходимости, вспомогательных параметров( например, коэффициента пропорциональности и др.), используя для этой цели дополнительные условия задачи.

6. Вывод общего закона рассматриваемого процесса и числовое определение искомых величин.

7. Анализ ответа и проверка исходного положения задачи [8].

В зависимости от характера задачи некоторые из данных рекомендаций могут отсутствовать.

При решении производственных задач с помощью дифференциальных уравнений требуется глубокое понимание сути изучаемых процессов.

Применяя алгоритмический подход, рассмотрим задачи, в которых фигурирует некоторая величина и скорость ее изменения.

Алгоритмы решения уравнений даны в приложениях [11].

В дальнейшем будет оговариваться, в соответствии с каким из предложенных алгоритмов будет решена задача.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Глава 2. Производственные задачи на составление дифференциальных уравнений

2.1. Задачи по физике

Задача 1

Из эксперимента известно, что скорость радиоактивного распада пропорциональна количеству вещества. Найти полупериод распада радиоактивного вещества (время, за которое распадается половина вещества), если при t=0, количество радиоактивного вещества было равно m₀  [14].

Решение

1)                    Искомая величина – это количество радиоактивного вещества. Обозначим его m.

Начальные условия:

При t=0 количество радиоактивного вещества равнялось m_0.

2)                    Так как количество радиоактивного вещества меняется с течением времени, его можно рассматривать как функцию от времени: m=m(t).

Скорость радиоактивного распада – это скорость изменения данной функции:

3)        По условию задачи , где k<0, так как с течением времени количество радиоактивного вещества уменьшается.

4)              Обозначим: t=x; m(t)=y(x);   

Получим уравнение    

5)        Уравнение       –  уравнение с разделяющимися переменными.

6)                    Решим уравнение на основании алгоритма 1[Приложение 1].

7)              – количество радиоактивного вещества в момент времени t.

8)                    При t = 0    m (0)= m₀, тогда

  частное решение при данных начальных условиях.

9)    Найдем период полураспада радиоактивного вещества Т: при t=T
           .

 Подставим эти значения в решение:

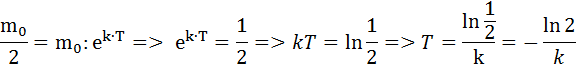
Ответ:

 

 

Задача 2

Температура вынутого из печи хлеба в течении 20 минут падает от 100 до 60. Температура воздуха равна 25. Через сколько времени от момента начала охлаждения температура хлеба понизится до 30? Учесть, что скорость охлаждения тела пропорциональна разности температур тела и окружающей среды [13].

Решение

1)                    Искомая величина у – температура хлеба в момент времени t.  Начальные условия: при t=0        y(0) = 100.

Дополнительные условия: при t = 20    у(20) = 60.

2)                    Так как температура хлеба меняется с течением времени, ее можно рассматривать как функцию от времени:  y = у(t).

Скорость охлаждения – это скорость изменения данной функции: .

По условию задачи

3)          , где , k0.

4)              Обозначим: t = x, y(t) = y(x),  .

5)                    Дифференциальное уравнение с разделяющимися переменными.

6)                    Решим уравнения на основании алгоритма 2[Приложение 2].

7)           - температура хлеба в момент времени t.

8)                    Воспользуемся начальными условиями: при t=0  y(0)=100

.

 ­­­– частное решение.

9)                    Воспользуемся дополнительными условиями: при t=0  y(20)=60.

     

 – частное решение при данных дополнительных условиях. Найдем момент времени, когда температура хлеба станет равной 30 .

Ответ:

 

Задача 3

Пусть тело брошено под углом α к горизонту с начальной скоростью .

Требуется вывести уравнение движения тела, пренебрегая силами сопротивления. Полагаем, что при t=0,  x=0,   y=0,    [4].

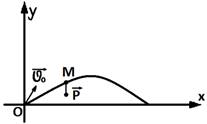Решение

Рис.1

Выберем оси координат, как показано на рисунке 1. В произвольном положении М на тело массой m действует лишь одна сила – его вес .

Поэтому в соответствии со вторым законом Ньютона дифференциальные уравнения движения в проекциях на оси ОХ и ОУ запишутся в виде:

(1)            и   (2)  (минус ставится в связи с тем, что m>0, g>0, но  

Разделив обе части на m, получаем:

  и  .

Оба уравнения решаем по алгоритму 6 [Приложение 6].

В результате получаем два общих решения:

     и     .

Воспользуемся данными начальными условиями: при t=0

x=0,y=0, .

Продифференцируем функции x(t)  и  y(t).

                            

                 

 

 

              

Тогда

  x(t)=               (1)

  y(t)=    (2)

Уравнения движения при заданных начальных условиях.

Теперь сделаем ряд выводов о характере движения тела.

1)                    Найдем, каково время полета тела до его падения на землю. Для этого нужно найти значение t, при котором у=0. Из () имеем.

t ( 

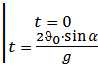
Время полета до падения на землю t =

2)                    Найдем, какова деятельность полета. Для этого воспользуемся соотношением (1) и вычислим значение функции x(t) при t, равном времени полета до падения на землю.

x (.

Из полученного результата видно, что дальность полета будет наибольшей при  .

При этом дальность равна .

3)                    Найдем максимальную высоту подъема. Для этого нужно найти максимальное значение y(t). Оно достигается, если    Из ( найдем

                                  .

Так как . Максимальная высота подъема .

4)          Выясним, какова траектория полета. Уравнения   и  являются параметрическими уравнениями параболы. Исключив из них t, получим

                       .

Траекторией полета является парабола.

Ответ:   

 

 

2.2. Задачи по теоретической механике

Задача 1

На материальную точку массы m действует постоянная сила, сообщающая точке ускорение . Окружающая среда оказывает движущейся точке сопротивление, пропорциональное скорости ее движения, коэффициент пропорциональности . Как изменится скорость движения со временем, если в начальный момент точка покоилась [13] ?

Решение

1)          Искомая величина  скорость движения точки.

Начальные условия:        t=0,  .

 

 

2)                    Так как скорость движения изменяется со временем, то ее можно рассматривать как функцию времени:  Скорость изменения этой величины или ускорение является скоростью изменения данной функции: .

 

 

 

 

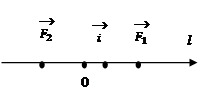
3)          Пусть точка движется в направлении L. Выберем единичный вектор  сонаправленный с L. В любой момент времени t на точку действуют 2 силы: постоянная сила   и  сила сопротивления среды . (рис.2)

Результирующая этих сил  может быть найдена по второму закона Ньютона как .

Таким образом, имеем векторное уравнение

В проекции на горизонтальную ось получаем дифференциальное уравнение

4)              .

5), 6) Это уравнение уже решено ранее по алгоритму 2;

его общее решение                  y(x)=c

        7)

8) Воспользуемся начальными условиями: при t=0,  

 

закон изменения скорости движения при данных начальных условиях.

10) При t   , то есть, если движение происходит достаточно долго, то его скорость приближенно можно считать постоянной.

Ответ: скорость постоянна

 

Задача 2

Точка массой m движется прямолинейно, на нее действует сила, пропорциональная времени (коэффициент пропорциональности ), протекшему от момента, когда скорость равнялась нулю. Кроме того, на точку действует сила сопротивления среды, пропорциональная скорости (коэффициент пропорциональности ). Найти зависимость скорости от времени [6].

Решение

1) Искомая величина – это скорость движения точки.

Начальные условия:

При t=0  скорость точки равнялась 0.

2) Так как скорость точки изменяется со временем, то ее можно рассматривать как функцию времени:  .

Скорость изменения скорости – это ускорение движения точки: .

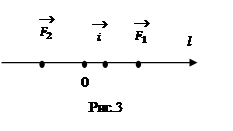
3) Точка движется прямолинейно в направлении L под действием двух сил:    и  . Их равнодействующая может быть найдена по второму закону Ньютона как  . (рис.3)

В проекции на горизонтальную ось получим дифференциальное уравнение: .

4) Обозначим t=x,

Получим     

5) Уравнение  – линейное дифференциальное уравнение первого порядка.

6) Решим уравнение, воспользовавшись алгоритмом 5 [Приложение 5].

7) Общее решение: скорость движения точки.

8) Найдем частное решение, воспользовавшись тем, что при t=0  :

0 =

скорость движения при данных начальных условиях.

10) Так как при t       , то можно считать, что при достаточно больших t скорость линейно зависит от времени.

Ответ: при t       , т.е. при достаточно больших t скорость линейно зависит от времени.

 

Задача 3

Пуля входит в доску толщиной 0,1 м со скоростью , а вылетает из доски, пробив ее, со скоростью  м/сек. Принимая, что сила сопротивления доски движению пули пропорциональна квадрату скорости движения, найти, сколько времени продолжалось движение пули через доску [14].

Решение

1)                    Искомая величина – это скорость движения пули. Обозначим ее ϑ.

Начальные условия: При t=0   скорость движения пули равнялась

  

2)                    Так как скорость пули изменяется с течением времени, ее можно рассматривать как функцию от времени: ϑ= ϑ(t).

Ускорение пули - это скорость изменения функции ϑ(t):

                                      .

3)                    На пулю, вошедшую в доску, по условию задачи, действует только сила сопротивления доски . С одной стороны, ее величина равна  а с другой стороны, по второму закону Ньютона, .

В проекции на горизонтальную ось имеем уравнение

  (минус в правой части уравнения приходится ставить в связи с тем, что  но  так как скорость пули при движении через доску уменьшается со временем).

4)          Обозначим:  t=x; ϑ(t)=(t);

Получаем дифференциальное уравнение .

5)          Уравнение уравнение с разделяющимися переменными.

6)          Решим уравнение в соответствии с алгоритмом   [Приложение 4].

7)          скорость движения пули в момент времени t.

8)          При t=0  тогда 200.

скорость пули при данных начальных условиях.

9)                    Зная скорость, можно найти величину пути, который проходит пуля за время t :

Так как при

Таким образом,

Найдем время , за которое пуля прошла сквозь доску.

Так как при  то из уравнения  имеем

 .

Известно также, что    .

Из   и   имеем 

 

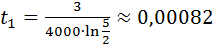(сек).

10) Следует отметить, что скорость движения пули сквозь доску обратно пропорциональна времени.

Ответ:  (сек)

 

2.3. Задачи по химии и технологии производства

Задача 1

В резервуаре имеется α кг водного раствора соли, в котором содержится b кг соли. В определенный момент включается устройство, непрерывно подающее в резервуар с кг чистой воды ежесекундно и одновременно удаляющее из него ежесекундно с кг раствора. При этом в самом резервуаре жидкость непрерывно перемешивается. Как изменяется со временем количество соли в резервуаре [2] ?

Решение

1)        Искомая величина – количество соли. Обозначим его .

Начальные условия. При t=0   количество соли равно b.

2)                    Так как количество соли в резервуаре меняется с течением времени, его можно рассматривать как функцию от времени:

3)          Дадим аргументу приращение

количество соли в момент времени  .

Приращение функции: величина, на которую уменьшается количество соли в резервуаре за время  t. 

(так как ).

4)                    Изменение количества соли может быть подсчитано и другим путем концентрация соли в момент t. Так как количество соли постоянно меняется, будем считать его равным   на протяжении времени ,

где a.

количество соли, вытекающее за время .

Имеем уравнение:      (  взято со знаком минус, так как < 0, а все величины в правой части уравнения положительные).

5)          .

6)        Перейдем к пределу при , в соответствии с алгоритмом 1 [Приложение 1].

7)               .

8)                    Получили дифференциальное уравнение с разделяющимися переменными вида .

9)           Решением этого уравнения являются функции вида:

10)           Перейдя к первоначальному названию переменных, получим:

11)    Найдем частное решение, воспользовавшись тем, что при t=0  

частное решение дифференциального уравнения.

12)       закон, по которому изменяется со временем количество соли  в резервуаре.

Так как    при  t   при  t

То есть при прошествии достаточно большого промежутка времени можно считать, что соль практически вымылась из резервуара.

Ответ:

Задача 2

В сосуд, содержащий 10 л воды, непрерывно поступает со скоростью 2 л в минуту раствор, в каждом литре которого содержится 0.3 кг соли. Поступающий в сосуд раствор перемешивается с водой, и смесь вытекает из сосуда с той же скоростью. Сколько соли будет в сосуде через 5 минут [16] ?

Решение

1)    Примем за независимое переменное время t, а за искомую функцию 

y (t) — количество соли в сосуде через t минут после начала опыта.  

Найдем, на сколько изменится количество соли за промежуток времени от момента t до момента t + Δt.  

2) В одну минуту поступает 2 л раствора, а в Δt минут — 2 Δt литров;

в этих 2 Δt литрах содержится     кг соли.  

С другой стороны, за время Δt из сосуда вытекает 2Δt литров раствора.  

3) В момент t во всем сосуде (10 л) содержится y(t) кг соли, следовательно, в 2Δt литрах вытекающего раствора содержалось бы      кг соли,  если бы за время Δt содержание соли в сосуде не менялось. Но так как оно за это время меняется на величину, бесконечно малую при  , то в вытекающих 2Δt литрах содержится

   кг соли, где  при .  

4) Итак, в растворе, втекающем за промежуток времени , содержится

0.6 Δ t кг соли, а в вытекающем   .

Приращение количества соли за это время  равно разности найденных величин, т. е.    

5) Разделим на Δt и перейдем к пределу при .  

В левой части получится производная y' (t), а в правой  при .  

Итак, имеем дифференциальное уравнение .

6)Решая его, получим  

7)Так как при t = 0 соли в сосуде не было, то   .

8)Полагая в (1) t = 0, найдем  .

9)Подставляя это значение C в (1), получим   

10)При t = 5 в сосуде будет   кг соли. 

Ответ:  кг

 

 

2.4. Задача по экономике

Задача 1

Предположим, что торговыми учреждениями реализуется продукция В, о которой в момент времени t из числа потенциальных покупателей N знает лишь покупателей. Предположим, что для ускорения сбыта продукции В были даны рекламные объявления. С большей степенью достоверности можно считать, что после объявления скорость изменения числа знающих о товаре покупателей пропорциональна как числу знающих о нем покупателей, так и числу не знающих о нем потенциальных покупателей. Считается, что отсчет времени ( t=0) начался в тот момент, когда о товаре знало   потенциальных покупателей. Найти закон изменения числа покупателей, знающих о товаре [2]?

Решение

1)          Искомая величина-это число покупателей, знающих о товаре .

Начальные условия: При t=0 число покупателей, знающих о товаре равно  .

2)                    Так как число покупателей, знающих о товаре, меняется с течением времени, то его можно рассмотреть как функцию от времени:  

Скорость изменения числа знающих о товаре – это скорость изменения данной функции: .

3)                    По условию задачи

4)              Обозначим: .

Получим уравнение  

5)          Уравнение     уравнение с разделяющимися переменными.

6)          Решим уравнение, пользуясь алгоритмом

7)          общий интеграл дифференциального уравнения.

8)              При . Отсюда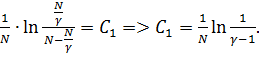 

Найдем частное решение, соответствующее данным начальным условиям.

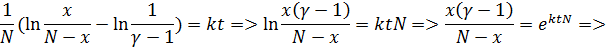
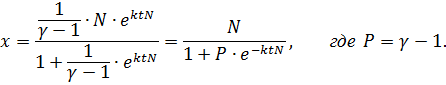
9)                    Уравнение     называется в экономической литературе логистической кривой. Приведем схематическое изображение этой кривой при  ( рис.4).

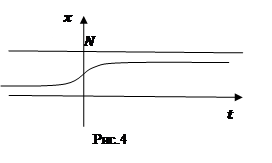
Очевидно, что при   число знающих о товаре покупателей стремится к числу всех потенциальных покупателей.

 

Ответ: при   число знающих о товаре покупателей стремится к числу всех потенциальных покупателей

 

Задача 2

Пусть заимодавец платит кредитору  процентов от занятой суммы  за год; сколько он должен уплатить за год на каждую единицу занятой суммы, если проценты нарастают непрерывно [5] ?

Решение

 Поскольку проценты нарастают непрерывно, то скорость (t) изменения величины долга   в момент времени t пропорциональна значению этой величины в тот же момент времени.

Следовательно, закон изменения долга описывается дифференциальным уравнением                                                              (1.1)                                         

Общим решением уравнения (1.1) является показательная функция

  = C

Поскольку ежегодный прирост величины   составляет , то скорость изменения величины составляет  от    и коэффициент  .

Кроме того, по условию задачи   = .

Поэтому сумма, которую заимодавец должен уплатить кредитору от занятых  денежных единиц за  лет, составит

  =     (1.2)

От каждой единицы занятой суммы заимодавец обязан уплатить

 = . А за год эта сумма составит  =  денежных единиц.

Уравнение (1.2) с     может быть применено не только при изучении кредитования. Оно применяется всякий раз, когда скорость изменения некоторой величины  прямо пропорциональна ее значению в данный момент времени , а ежегодный прирост равен  .

Ответ: за год эта сумма составит   =   денежных единиц

Задача 3

В настоящее время для обеспечения пищей одного человека необходима площадь 0, 1 га.

На земном шаре 4 000 млн. га пахотной земли. Поэтому население его должно быть, если не учитывать в будущем новых источников пищи, ограничено количеством 40 000 млн. человек.

Когда будет достигнут этот предел насыщения населения, если оно непрерывно растет со скоростью 1, 8% в год [9] ?

Решение

Согласно формуле (1.2), закон роста населения можно выразить следующим образом:                                          y(t) =  

За t = 0 возьмем 1999 год, когда население Земли составило 6 ·  человек.

Тогда y(t) = 6 ·

Ищем такое t, чтобы y(t) = 40 · .

Тогда 40 ·  = 6 · · .

Откуда  ·  =  ≈ 6,667.

Логарифмируя последнее равенство, имеем

 ≈ ln 6,667 ≈ 1,897.

Откуда t ≈ 105 лет

Ответ: 105 лет

 

 

 

 

 

 

 

 

Заключение

 

В проделанной работе были рассмотрены обыкновенные дифференциальные уравнения и реальные производственные задачи, которые решаются с их помощью.

     Было показано, что обыкновенные дифференциальные уравнения применяются для описания многих процессов реальной действительности. Трудно представить себе область науки или производства, в которой не возникала бы необходимость использования дифференциальных уравнений.

Таким образом, проделанная работа показала важность применения обыкновенных дифференциальных уравнений при математическом моделировании конкретных производственных задач из разных областей: физика, теоретическая механика, экономика, химия и технология производства.

Вследствие вышесказанного можно сказать, что цель курсовой работы была достигнута и  поставленные задачи выполнены.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список использованных источников и литературы

 

1. Агафонов, С.А. Дифференциальные уравнения  С.А.Агафонов, А.Д. Герман, Т.В.Муратова.  М.: МГТУ им. Н.Э. Баумана, 2004, —348 с.

2. Амелькин, В.В. Дифференциальные уравнения в приложенияхВ.В.Амелькин.­  М.: Наука, 1987, —160 с.

3. Данилов, А. М. Дифференциальные уравнения А.М.Данилов, Г.Д. Фадеева.  Пенза: ПГАСА. 1997. — 144 с.

4. Демидович, Б.П. Задачи и упражнения по математическому анализу для ВТУЗов Б.П.Демидович. М.: АСТ, 2001—496 с.

5. Дмитриева, А. Б. Самостоятельная работа по решению прикладных задач в курсе математики как условие повышения качества профессиональной подготовки обучаемых в вузе А.Б.Дмитриева.  М.: , 2004. – 18 с.

6. Зайниев, Р. М. Задачи и упражнения по математике с практическим содержанием: учебное пособие для студентов, обучающихся по направлениям и специальностям техники и технологии Р.М.Зайниев.  2008. – 80 с.

7. Зайцев, В.Ф. Справочник по обыкновенным дифференциальным уравнениям  В.Ф.Зайцев, А.Д.Полянин. – М.: Физматлит, 2001 — 576 с.

8. Ильин, В.А. Основы математического анализа: в 2-х частяхВ.А.Ильин. М.: Физматлит, 2009, —647с.

9. Краснов, М.Л. Обыкновенные дифференциальные уравнения: Задачи и примеры с подробными решениями: Учебное пособие. Изд. 4-еМ.Л.Краснов, А.И.Киселев, Г.И.Макаренко.  — М.: Едиториал УРСС, 2002. — 256 с.

10. Никольский, С.М. Курс математического анализаС.М.Никольский  – М.: Физматлит, 2001, —592с.

11. Новак, Н.М., Методические указанию по решению задач на составление обыкновенных дифференциальных уравненийН.М.Новак. Оренбург, 1991, —31 с.

12. Пискунов, Н.С. Дифференциальное и интегральное исчисленияН.С.Пискунов.  – М.: Интеграл-Пресс, 2004. —544 с.

13. Пономарев, К.К. Составление и решение дифференциальных уравнений инженерно-технических задачК.К.Пономарев.  – М.: Учпедиз, 1962 —184 с.

14. Самойленко, А.М. и др. Дифференциальные уравнения. Примеры и задачи  А.М.Самойленко. – Киев, Высшая школа, 1989, —383 с.

15. Тихонов, А. Н. Дифференциальные уравнения: Учеб.: Для вузов А.Н.Тихонов, А.Б.Васильева, А.Г.Свешников.— М.: ФИЗМАТЛИТ, 2005. — 256 с.

16. Филиппов, А.Ф. Сборник задач по дифференциальным уравнениям А.Ф.Филиппов. – М.-Ижевск: Изд. РХД, 2000. — 496 с.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЯ

АЛГОРИТМЫ РЕШЕНИЯ УРАВНЕНИЙ

 

ПРИЛОЖЕНИЕ 1

АЛГОРИТМ  1

                     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 2

АЛГОРИТМ  2

 

 

        

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 3

АЛГОРИТМ 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 4

АЛГОРИТМ  4

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ 5

АЛГОРИТМ  5

	Будем искать решение данного уравнения в виде    функция
			Из неравенства полученного  в

 

 

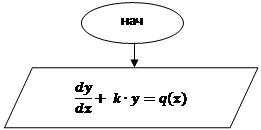                           1)

 

Составить для данного уравнения однородное

                 

              2)

 

Решением уравнения, полученного в  будет, согласно алгоритму , где С - const

    

  3)

 

               4)

 

 

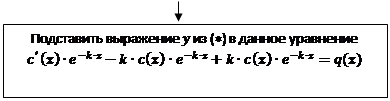              5)

 

 

                     6)

 

                     7)

 

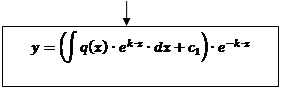
                      8)

 

 

 

ПРИЛОЖЕНИЕ 6

АЛГОРИТМ  6

 

 

                1)

 

 

             2)

 

 

             3)

 

 

              4)