ТЕСТ ПО АЛГЕБРЕ 7 класс Тема: «Разложение многочленов на множители»

ТЕСТ  ПО  алгебре,  7 класс

Тема:  «Разложение многочленов на множители» Цель: проверка знаний учащихся по данной теме.

Уровень сложности: с 1 по 20 – базовый, с 21 по 30 – повышенной сложности. Время на выполнение одного тестового задания 3 мин.

Инструкция по выполнению работы

На выполнение работы дается  90 мин. Работа состоит из двух частей. В части А - 20 заданий  с выбором ответа (один верный ответ из четырех предложенных). С помощью заданий с выбором ответа проверяется базовый уровень подготовки по теме. В части Б – 10 заданий, на которые надо найти ответ. Данная часть направлена на дифференцируемую проверку повышенного уровня владения программным материалом.

В бланке теста отмечать правильный ответ или делать какие-либо пометки запрещено. Выбранный ответ необходимо отметить на отдельном бланке ответов.

Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднения, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.

За выполнение задания дается один балл. Баллы, полученные вами за выполненные заданий, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Часть  А.

1. Слагаемые имеют общий множитель в многочлене:

1) 3xy – 5x     2) 6a + 7b         3) m + mn + n             4) x² – y²

2. Верным является равенство:

1) 7bx + 5by = 7b(x +5by)                  2) 7bx + 5by = 35b(x +y)

3) 7bx + 5by = b(7x +5y)                    4) 7bx + 5by = 35b(x +by)

3. Вынести за скобку общий множитель: 5x – 10y.

1) 5(x – y)         2) 5(x – 2y)               3) 5(x + 2y)          4) 2(x – 5y)

4. Разложением многочлена 3x +3y – bx – by  на множители является

1) (3 – b)(x +y)        2) (x –y)(3 +b)      3) 3b(x +y)            4) -3b(x – y)

5. Представить в виде произведения многочлен 10ax – 4ay +5cx – 2cy.

1) (5x – 2y)(2a + c)             2) (5x +2y)(c – 2a)

3) (2a +c)(5x + 2y)              4) (2a – c)(5x – 2y)

6.                 Представить трёхчлен  1+ 6x +9x²  в виде квадрата двучлена. 1) (1 – 3x)(1 +3x)   2) (1 – 3x)²      3) (1 + 3x)²         4) (1 + 9x)²

7.                 Какой одночлен необходимо вписать вместо знака  *, чтобы трёхчлен  * - 4ax +4a² можно было представить в виде квадрата двучлена?

1) 1         2) x²            3) x              4) 2x

8. Разложить на множители многочлен  -64 + a²

1) (-8 + a)(-8 – a)          2) (a – 8)(a + 8)      3) (a – 8)²          4) (-64 + a)²

9. Представить в виде произведения многочлен  0,09t² – 121p².

1) (0,3t – 11p)                                    2) (0,3t + 11p)

3) (0,9t – 121p) (0,9t + 121p)            4) (0,3t – 11p) (0,3t + 11p)

10. Разложить на множители многочлен (m – n)a + (n – m)b.

1) (m – n)(a + b)      2) (m – n)(a - b)     3) (n - m)(a + b)     4) (n - m)(a - b)

11. Вычислить: 25² - 15².

1) 850        2) 400           3) 1600        4) 100

12. Разложить на множители многочлен 27 – a³y⁶.

1) (3 – ay²)³                                         2) (3 – ay²)(9 – 3ay² + a²y⁴)

3) (3 – ay²)(9 + a²y⁴)                           4) (3 – ay²)(9 + 3ay² + a²y⁴)

13. Значение выражения 17,2 · 8,1 +23,8 · 5,1 – 17,2 · 7,6 – 23,8 · 4,6 равно:

1) 20,5                           2) 20                   3) -1          4) -20,5 

14. Значение выражения x³ – 9x²  + x – 9 при  x = 19 равно:

1) 200                    2) 0                 3) 3620                4) 3610

15. Разложить на множители: 14 – 14m².

1) 14(1 – m²)    2) (14 – m)(14 + m)     3) 14(1 – m)(1 + m)     4) 14( - m²)

16. Представить в виде произведения:  a² – 2ab + b² – 25.       

1) (a – b)²(b – 5)(b +5)               2) b(a – 5)(a + 5)(2a – b)

3) (a² + b²)(2ab + 25)                 4) (a – b – 5)(a – b + 5)

17.  Корни уравнения 6x² – 24x = 0 равны:

1) 0; 4         2) -4; 0            3) 0            4) 4

18. Сумма корней уравнения  x(x – 15) + 3(x – 15) = 0 равна:

1) 15               2) 18              3) 12           4) -12

19. Корнями уравнения  x² + 4x + 4 = 0 являются числа:

1) -2                2) 2                3) -2; 2                 4) 0; -2

20. Значение выражения 17² - 34· 7 +7² равно:

1) 10        2) 34          3) 100                 4) 576

  Часть Б.

21.  Найти корни уравнения x⁴ + 6x³ = 0.

22.  Представить в виде произведения: xⁿ⁺¹ + xⁿ.

23.  Разложить на множители трёхчлен x² – 5x + 4.

24.  Решить уравнение :  y⁴ – 3y³ + y = 3.

25.  Найти наименьший корень уравнения  (2y + 1)(y² – 6y + 9) = 0

26.  Представить в виде произведения  x²ⁿ⁺⁸ + 10xⁿ⁺⁴ + 25.

27.  Вычислить: 2⁹⁰ · 3³⁰ – (24¹⁵ – 3)(24¹⁵ + 3).

28.  Разложить на множители 16x² – 24xy + 9y² – 4x + 3y.

29.  Вычислить: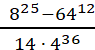   

30.  При каком значении а значение выражения  8а³ – 4а² + 2а – 1 равно 0?

Инструкция по проверке тестовых задания

За каждое верно выполненное задание учащийся получает 1 балл. Максимальное количество баллов – 30. Оценка определяется исходя из следующих показателей:

-  от 27 до 30 баллов – оценка «5»

-  от 22 до 26 баллов – оценка «4»

-  от 16 до 21 балла – оценка «3»

-  15 и менее баллов – оценка «2»

Бланк ответов части А.

                                                         Бланк ответов части  Б.