Ю. П. Дудницын В. Л. Кронгауз

	АЛГЕБРА Тематические тесты
	класс

2-е издание

Москва

«Просвещение»

2011

удк 372.8:512 ББК 74.262.21

Д81

Дудницын Ю. П.

Д81 Алгебра. Тематические тесты. 9 класс / Ю. П. Дудницын, В. Л. Кронгауз. — 2-е изд. — М. : Просвещение, 2011. 95 с. : ил. ISBN 978-5-09-026140-1.

Пособие является частью учебно-методического комплекта по алгебре для 9 класса Ю. Н. Макарычева и др. В комплект входят также дидактические материалы и книга для учителя авторов Ю. Н. Макарычева и др. и поурочные разработки авторов В. И. Жохова, Л. Б. Крайневой.

Пособие содержит тесты по важнейшим разделам курса алгебры 9 класса основной школы. С их помощью можно осуществлять тематический контроль знаний девятиклассников и подготовку к Г ИА.

удк 372.8:512 ББК 74.262.21

ISBN 9786-09-026140-1 С) Издательство «Просвещение», 2009 С) Художественное оформление.

Издательство «Просвещение», 2009

Все права защищены

Предисловие

Предлагаемое пособие подготовлено для учителей математики, которые используют в настоящее время при изучении курса алгебры 9 класса в качестве основного учебник «Алгебра. 9 класс» Ю. Н. Макарычева и других авторов под редакцией С. А. Теляковского 15-е и последующие издания (М.: Просвещение). Этот учебник является переработанным вариантом аналогичного пособия «Алгебра. 9 класс» тех же авторов издания до 2007 г. Значительной переработке подверглись как его содержание, так и структура.

В пособии содержится восемь тематических тестов по важнейшим разделам курса алгебры основной школы и один итоговый тест. С их помощью можно осуществлять тематический контроль знаний девятиклассников, а также проверять уровень усвоения всего курса алгебры 9 класса в конце учебного года.

Каждый тест дан в четырех вариантах примерно одинаковой трудности. Их содержание приведено в соответствии с Обязательным минимумом содержания образования по математике в основной школе. При составлении конкретных заданий каждого теста авторы руководствовались идеологией требований к уровню подготовки учащихся, сформулированных в новых образовательных стандартах.

Структура предлагаемых тестов, формулировки многих заданий, форма их предъявления идентичны тем, которые приведены в сборниках для государственной (итоговой) аттестации по алгебре в 9 классе в новой форме, опыт проведения которой широко распространен в настоящее время в школах России.

Содержательные и конструктивные особенности экзаменационных материалов предполагают наличие у школьников умений оперировать с текстами подобных заданий, понимать требования к записи полученного или выбранного ответа, форме и объему промежуточных выкладок. Учащимся предстоит научиться правильно распределять время на выполнение различных заданий.

з

Многие учителя понимают необходимость систематического формирования таких умений не только в последние недели учебного года, а в течение всего учебного процесса. Чтобы оказать помощь учителю в успешном решении этой сложной и новой проблемы, авторы предлагают приводимые в пособии материалы.

Каждый тест состоит из двух частей: части 1 и части 2. В первой части тестов 1—8 содержится шесть заданий с выборкой верного ответа из приведенных четырех вариантов. Два или три задания девятиклассники могут выполнять устно, записав только номер выбранного ответа. Для выполнения остальных заданий этой группы дОСтаточно привести весьма краткие математические выкладки или необходимые схемы. Учитель может их не проверять, ибо они носят вспомогательный (черновой) характер. Основное требование к учащемуся точно указать номер верного ответа. Успешность выполнения первой группы заданий отражает степень овладения материалом на обязательном уровне.

Вторая часть всех тестов (кроме теста 9, итогового) содержит три задания. Они сложнее заданий первой части, так как выполняются в несколько этапов, а не в один-два шага. Для успешного их выполнения не требуется дополнительных знаний, выходящих за пределы программы основной школы. Подобные задания часто рассматриваются в учебнике, и соответствующие навыки и умения отрабатываются в классе под руководством учителя. Все необходимые выкладки учащиеся выполняют в тетрадях подробно и аккуратно, при необходимости сопровождают их пояснениями. Учитель проверяет правильность решения и полученного ответа.

Последнее задание каждого теста позволяет девятикласснику проявить высокий уровень знаний, интерес к предмету, способность применить знания в нестандартной ситуации. Однако выполнение подобных заданий не предполагает обязательного владения материалом из дополнительных разделов алгебры. Они так же, как и все остальные, проверяют усвоение программного материала. Подробные решения и ответ записываются в тетрадь.

Перечисленные особенности тестов влекут за собой необходимость корректировки привычной, • традиционной системы выставления оценок.

Оценку «5» целесообразно ставить в следующих случаях: 1) при верном выполнении всех заданий; 2) при верном выполнении восьми заданий и наличии ошибки в ответе к одному из первых шести заданий; З) при верном выполнении восьми заданий, но при указании на верный путь решения в записях к последнему заданию.

Оценку «4» целесообразно ставить в таких случаях: 1) при верном выполнении восьми заданий; 2) при верном выполнении семи заданий и наличии указания на верный путь решения в одном из заданий второй части.

Оценку «З» целесообразно ставить: 1) при верном выполнении пяти или шести заданий; 2) при верном выполнении шести заданий и найденном верном пути решения одного из заданий второй части.

Желательно учесть индивидуальные особенности учащегося и поощрить его или предъявить к нему повышенные требования при выставлении оценки «З» или «4».

В настоящее время используется и другая — рейтинговая система оценивания работ школьников. В этом случае за верное выполнение задания выставляется определенное количество баллов и результатом (оценкой) служит сумма набранных баллов во всех заданиях. Для удобства подсчета можно выставлять за каждое верно выполненное задание первой части 1 балл, за задание второй части 2 балла, а за последнее задание 4 балла. И за верно найденный путь решения (при наличии в нем какой-либо ошибки) в задании второй части — 1 балл, в последнем задании — 2 балла. Теперь легко можно перевести систему оценок из пятибалльной в рейтинговую: «5» 14—12 баллов, «4» 11 9 баллов, «З» 8—5 баллов, «2» — 4—0 баллов.

Отметим, что каждый учитель сам выбирает ту или иную систему оценивания в зависимости от условий, в которых оказываются его ученики. Важно довести до каждого девятиклассника общий уровень требований, который ясен для них с самого начала учебного года и будет предъявляться им при выполнении всех работ. Получив тест, каждый девятиклассник сможет примерно оценить свои возможности и, закончив работу, дать самооценку качества ее выполнения до проверки учителем.

Авторы обращают внимание учителя на содержание теста 8 по теме «Элементы комбинаторики. Начальные сведения из теории вероятностей». Этот материал впервые включен в учебник 9 класса и становится обязательным для изучения. В школах еще не накоплен опыт изложения нового материала, формирования умений решать разнообразные задачи по теме. У девятиклассников могут возникнуть трудности в усвоении основного содержания. В этом случае можно воздержаться от проведения теста 8 в полном объеме. Возможно, учитель использхтет предлагаемые в нем задания для составления одной или двух СаМОСТОЯтельных проверочных работ на 20 минут. В каждую из них целесообразно включить 4—5 заданий соответствующего содержания.

Остановимся на структуре итогового теста 9 (годовой контрольной работы). Он рассчитан на 2 урока и содержит 8 заданий в части 1 и 5 заданий в части 2. Будем считать эту работу годовой по курсу алгебры 9 класса. По этой причине не следует считать ее итоговой по алгебре за курс основной школы, так как в ее содержание не включены многие важные разделы 7—8 классов. Вопрос о целесообразности ее проведения по окончании изучения материала 9 класса учитель решает сам в зависимости от наличия учебного времени на повторение курса и организации подготовки к итоговой аттестации по алгебре за курс основной школы. Возможный вариант рейтинговой-оценки выполнения теста 9: «5» — 20—18 баллов, «4» — 17—13 баллов, «З» — 12—7 баллов, «2» 6—0 баллов.

Такой подход к системе оценивания результатов значительно повышает информативность каждой оценки. Они более точно характеризуют уровень усвоения учебного материала по каждой теме. У учителя появляется возможность предлагать каждому девятикласснику для контроля материал, соответствующий его уровню подготовки и поэтому доступный для него. Тем самым создается больше возможностей для реализации в процессе обучения основных принципов уровневой дифференциации. Учителю удается обеспечить достижение всеми девятиклассниками базового уровня подготовки по алгебре и в то же время обеспечить усвоение материала на более высоком уровне теми, кто проявляет повышенный интерес и склонности к предмету. Таким образом, продвигается решение вопроса о предпрофильной подготовке в 9 классе.

Авторы выражают искреннюю благодарность учителям математики Центра образования № 345 Москвы Е. Б. Довгалюк, И. Е. Карелиной, Л. Ю. Ревиновой и О. А. Померко за апробацию работ, ценные предложения и замечания.

Авторы

Тест 1

Вариант 1

ЧАСТЬ 1

[2 Найдите область определения функции у — З

любое число

[Ц Какая функция имеет нули?

                     5                            

                                               х

З] Найдите все значения х, при которых значение функции у = х² — 4х равно -3.

                                    4) таких значений нет

[Д] Сократите дробь

              х                                              х

      1)                                          2)

      3)                                          4)

3х-3

5] В какой точке пересекаются ось абсцисс и ось симметрии графика функции у = х² + 4х — 5?

-2

Изобразите схематично график            у = —х² — 4х — З. В какой          нет точек этого графика?

4) IV

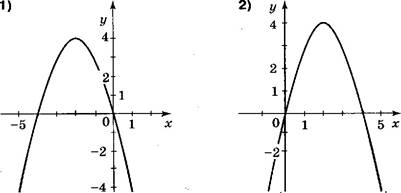
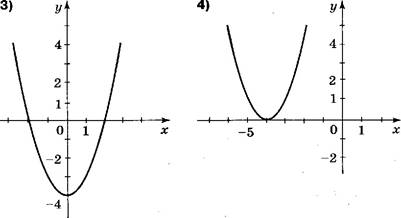
При каком значении х выражение 0,5х ² — 3х + 4 принимает наименьшее значение?

Ответ:

[0 Найдите все т, при которых график функции у = т 2х — 3х ² с осью абсцисс две общие точки.

Ответ:

Тест 1                                            Вариант 2

ЧАСТЬ

[2 Найдите область определения функции у —

любое число

[Ц Какая функция не имеет нулей?

9 —х2 х

[З Найдите все значения х, при которых значение функции у = х ² — 2х равно З.

                                      4) таких значений нет

а ² + ба

Сократите дробь -

0 ² +5а—6

                 а                                         а

        1)                                      2)

       3)                                4)

5а—5

В какой точке пересекаются ось абсцисс и ось симметрии графика функции у = —х ² + 4х — З?

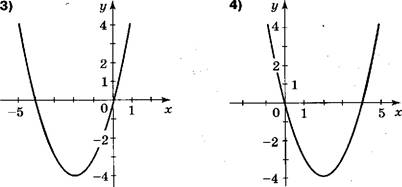
В Изобразите схематично	у = х 2
— 6х + 5. В каких	расположе-

ны точки этого графика?

При каком значении х выражение —1,5х ² + 6х — 4,5 принимает наибольшее значение?

Ответ:

[9 Найдите все К, при которых график функции у = 2х х + К не с осью абсцисс ни одной общей точки.

Ответ:

Тест 1                                           Вариант З

5

Найдите область определения функции у —

— любое число

[Ц Какая функция имеет нули?

  х-6              х

Найдите все значения х, при которых значение функции у = х? — 5х равно —6.

                                    4) таких значений нет

[Д Сократите дробь    •

х2 —8х+15

      1) х                             2) х

8х-15

      3)                                            4) х

х-з

[З В какой точке пересекаются ось абсцисс и ось симметрии графика функции у = х ² — 6х + 5?

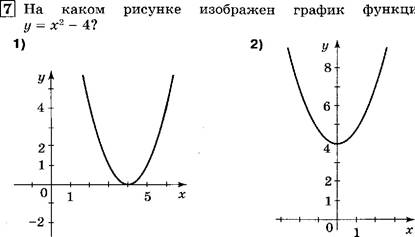
В Изобразите схематично	у = х?
— 4х + З. В какой го графика?	нет точек это-

4) IV

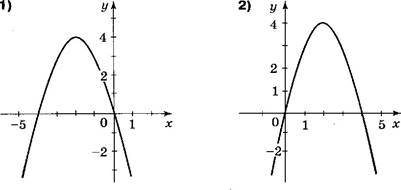
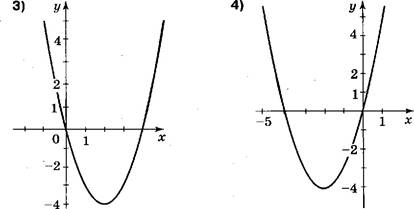
При каком значении х выражение О, 5х ² — х — 4 принимает наименьшее значение?

Ответ:

9] Найдите все у = 6х 6х + т

Ответ:

т, при которых график функции с осью абсцисс две общие точки.

Тест 1 Вариант 4 [Щ Найдите область определения функции у =              • Х -1-5  — любое число   [2] Какая функция не имеет нулей?                            7 Найдите все х, при которых значение функции у = х 2 — 6х равно —5.                                     4) таких значений нет Д Сократите дробь       1)                                          2) с с В какой точке пересекаются ось абсцисс и ось симмет-

рии графика функции у = х ² — 4х — 5?

Изобразите схематично  6х — 5. В каких ны точки этого графика?

у = —х ² расположе-

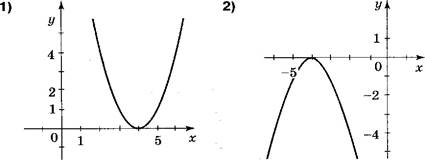
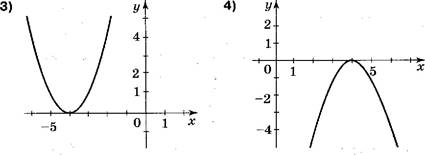
В] При каком значении х выражение 0,5х ² + х + 1,5 принимает наибольшее значение?

Ответ:

[0 Найдите все значения d, при которых график функции у = 4х 8х + d не имеет с осью абсцисс общих точек.

Ответ:

Тест 2                                                                                              1

ЧАСТЬ 1

[2 Вычислите значение выражения ⁴ 625 - ⁵ 32

2] Вычислите значение выражения 0,16 -4- З -3-з

Найдите область определения выражения 6 4—х.

                                    4) [4; +00)

Д] Дана функция у = х¹⁷ . Какое из утверждений верно?

1) у (4,1) ку (3,9) 2) у (-11,2) (-0,8) 3) у  (3,1) 4) у (-3,1) = у (3,1)

[5 Решите уравнение (х⁴ - 16) (х⁵ - 5) = о.

          5 5                  

43

[Ч Среди                     6, 200, 200, 40                        наибольшее.

2)          200

3)          ^з 200

.r ⁸ 3х + 4? (Ответ поясните с помощью соответствующих графиков функций.)

Ответ:

Решите уравнение х ⁴ + х? = 12

Ответ:

[В Решите уравнение 4у³ — 7 —- У - 28у2.

Ответ:

Тест 2

2

ЧАСТЬ 1

Д] Вычислите значение выражения ^з 125- ⁴ 81

[Ц Вычислите значение выражения 4 5 1       «623.

 16

[З Найдите область определения выражения 11—х.

2) [11; +00)  4) (-11; +00)

[Д Дана функция у = х 12 1) у  (4,9) 3) у (-2,03) у (2,03)

Какое из утверждений верно? 2) у (-3,3) > (-4,5) 4) у (-2,03) = у (2,03)

[З Решите уравнение (х⁶ — 64) (х^з - 6) о.

2 з

      Среди             5, 4 600,       600, ³ 160                  наибольшее.

                                     2) к 600

3) чббб

2 Лучнилп,пк

.x ⁷ —х? (Ответ поясните с помощью соответствующих графиков функций.)

Ответ:

Решите уравнение х ⁴ — х ² = 12.

Ответ:

ф] Решите уравнение (х + 4) (х — — (х —  - 0.

Ответ:

Тест 2

ЧАСТЬ 1

[Щ Вычислите значение выражения

[Ц Вычислите значение выражения

3) 0,157

З

81- ³ 216.

2 ¹4 з$6766.

25

[З Найдите область определения выражения

                              4) [0; +00)

Дана функция у = х^а . Какое из утверждений верно?

      1) у (6,07)        (5,8)          2) у                 у (-2,9)

      3) у (-3,01) = у (3,01)        4) у (-3,01) у (3,01)

Решите уравнение (х^б

2

3'

     Среди                  7, 350, 03, 35                       наименьшее.

      4                                        4) ^з 350

х ⁹ 2 — х? (Ответ поясните с помощью соответствующих графиков функций.)

Ответ:

Решите уравнение t ⁴ — 21t ² = 100.

Ответ:

Решите уравнение (х ² + 14х — 64) ² —4х + 16) ² .

Ответ:

     тест 2                                                                                            4

ЧАСТЬ 1

[Щ Вычислите значение выражения 64-4 243.

    [Ц Вычислите значение выражения             + —155

3) -2,38

[З Найдите область определения выражения

           1) [7; +00)                           

                                     4) (7; +00)

[Д Дана функция у = ..r 1 5 1) у (3,2) ку (3,7)         3) (-1,5)          (1,5)

Какое из утверждений верно? 2) у (-8,3) > у (-7,9) 4) у (-1,5)             (1,5)

Решите уравнение (х⁴ — 8) (х⁵ + 32) = о.

   [Ц Среди                 4, 100, 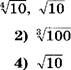                 наименьшее.

х12 5 — х? (Ответ поясните с помощью соответствующих графиков функций.)

Ответ:

Решите уравнение х ^з + 28 = 7х ² + 4х.

Ответ:

[О Решите уравнение (х ² — 4х) ² + 9х² = 36х — 20

Ответ:

Тест З                                                                                              1

ЧАСТЬ 1

[2 Сколько целых чисел являются решениями неравенст-

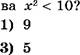
[2 На каком рисунке изображено множество решений неравенства (х + 4) (х — 1) О?

1)                                                         2)

1                     4          х	1                 4             х
3)	4)
zzzz«zzvzzzzcz,	czzzzzzzzzzzzza
1      х	—4                1

Решая неравенство второй степени, ученик верно построил график соответствующей функции и изобразил множество его решений. Какое неравенство ему было предложено?

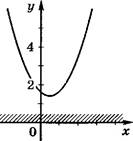1) ах² + bx + с > 4

ах² bx с

ах² bx с > О

[3

—х² + 3х + 4 расположены выше оси абс-

цисс.

З) (—оо; —4) U (1; +00) [З Решив уравнение

4) (-оо; -4] [1; +00) = 1 + х, укажите, в каком проме-

1—х жутке расположены его корни.

Решите неравенство (х² — 3х) (х + 2) О методом интервалов.

         1) [—2; 0] U [3; +00)        

ЧАСТ Ь 2

[2 Найдите область определения функции

х

Ответ:

Найдите все значения Ь, при которых уравнение О имеет два корня.

Ответ:

Решите уравнение

Ответ:

Тест З

2

ЧАСТЬ 1

Д] Сколько целых чисел являются решениями неравенства х² 16?

[Д На каком рисунке изображено множество решений неравенства

     1)                                                          2)

zzzzzzzzzu

—5

     3)                                                          4)

vzzzzzzzcza«zzzzzwzu.

                                              х                               о          5          х

х10 -2	х

Решая неравенство второй степени, ученик верно построил график соответствующей функции и изобразил множество его решений.

Какое неравенство ему было предложено?

1) ах² + bx + с О ах² 6х с ах? bx с

[Д

х ² — х — 6 расположены выше оси абсцисс.

           3) (-оо; -2] и [3; +00)          4) (-оо; -3] и [2; +00)

Решив уравнение = 2х — 1, укажите, в каком промежутке расположены его корни.

Решите неравенство (х² — 3х) (х + 2) О методом интервалов.

2)          И [З; +00) 4) [0; +00)

ЧАСТЬ 2

[З Найдите область определения функции

Ответ:

Найдите все значения а, при которых уравнение х ² — 4ах + 4 = О не имеет корней.

          Ответ:

2 Решите уравнение

Ответ:

тест З                                                                                              З

ЧАСТЬ

[Щ Сколько целых чисел являются решениями неравенст-

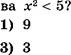
2] На каком рисунке изображено множество решений неравенства (х — 2) (х + З) О?

1)	2)
«zzzzzzzzzzzzzzzzz	czzzzzzzvzzzzzu,
-2            з	-3                2
3)	4)

czzzzwzzza

                                                      -2             з         х

	х

Решая неравенство второй степени, ученик верно построил график соответствующей функции и изобразил множество его решений. Какое неравенство ему было предложено?

1)                     ах² + bx + с» О

              ах² bx             О

ах² Ьх с > О

[Д

—х ² + 2х — 3 расположены ниже оси абсцисс.

                                                          4) (—оо; —3) И (1; +00)

Решив уравнение — З— х, укажите, в каком промежутке расположены его корни.

Решите неравенство (х — 5) (х ² — 4) О методом интервалов.

2)                     2] U [5; +00) 

4) (-оо; 2] U [5; +00)

ЧАСТЬ 2

Найдите область определения функции ,f(x) = х-2

Ответ:

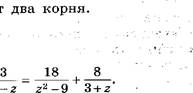Найдите все значения т, при которых уравнение х ² + 2тх + зт = О имеет два корня.

Ответ:

[В Решите уравнение 1 —

Ответ:

    Тест З                                                                                               4

часть

[Щ Сколько целых чисел являются решениями неравенства х² 9?

[В На каком рисунке изображено множество решений неравенства (х + 6) (х — 1) О?

1)    2) ccuzuzzzzzu.vzzz«zzzzzzzvzu. -6       1              х              -1             6             

      3)                                                      4)

	х

[З] Решая неравенство второй степени, ученик верно построил график соответствующей функции и изобразил       множество     его решений. Какое неравенство ему было предложено?

1) ах² + bx + с О

2) ах2	bx	с —4
З) ах2	bx	с > О

4) ах

х² + 4х — 5 расположены выше оси абс-

цисс.

      +00)                        4) (-оо; -5) U (1; +00)

Решив уравнение  = х— 2, укажите, в каком промежутке расположены его корни.

Решите неравенство х (х — 4)(х + 5) О методом интервалов .

                    0] и [4; +00)         

4) [0; +00)

ЧАСТЬ 2

[2 Найдите область определения функции f(x) =

Ответ:

Найдите все значения t, при которых уравнение х? — tx — 2t = О не имеет корней.

Ответ:

[О Решите уравнение 2

зо

Тест 4                                           Вариант 1

ЧАСТЬ

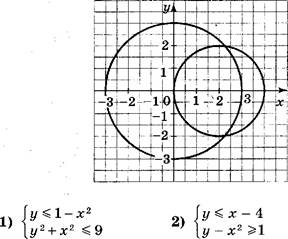
Какая пара чисел является решением системы урав-

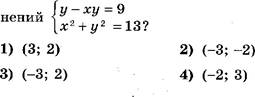
[2] На рисунке изображены графики функций у = f (х) и у = g (х). Сколько решений имеет система уравнений

	2
—4		5

С помощью графиков найдите число решений системы ху = 2 у —х ² = 1.

                        систему               

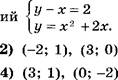
б] Пусть (231 ; У1) — решение системы уравнений

= 18.

Вычислите х 1 + у 1 , не решая этой системы.

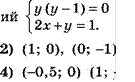
Решите систему уравнений

3) (0,5; 0), (0; 1)

ЧАСТЬ 2

[2 Найдите все значения параметра Ь, при которых систе-

ма уравнений имеет одно решение.

Ответ:

Составьте систему уравнений для решения задачи: «Площадь прямоугольника равна 24. Квадрат длины его диагонали — 73. Чему равен периметр прямоугольника?»

Ответ:

Вычислите периметр прямоугольника по условию зада-

чи 8.

Тест 4                                             Вариант 2

ЧАСТЬ

[Щ Какая пара чисел является решением системы уравне-

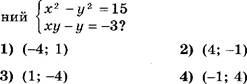
[Д На рисунке изображены графики функций у = f (х) и у = g (х). Сколько решений имеет система уравнений

у = g(x)?

	—4		х

С помощью графиков найдите число решений системы

З Дуднииын

   [Щ                 систему               

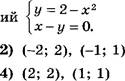
б] Пусть (х, ; .џ1) — решение системы. уравнений

         х = 20.

Вычислите  — Щ, не решая этой системы.

Решите систему уравнений

1) (0; 2), (3; 0,5)

3) (0; -2), (3; -0,5)

ЧАСТЬ 2

Найдите все значения параметра т, при которых систе-

ма уравнений  имеет одно решение.

Ответ:

Составьте систему уравнений для решения задачи: « Площадь прямоугольного треугольника равна 18. Квадрат длины его гипотенузы 97. Чему равна сумма длин катетов данного треугольника? »

Ответ:

9] Вычислите сумму длин катетов треугольника по условию задачи 8.

Тест 4                                                                                              З

Е] Какая пара чисел является решением системы уравне-

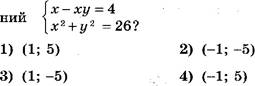
[Д На рисунке изображены графики функций у = f (х) и у = g (х). Сколько решений имеет система уравнений

у = g(x)?

-2 -2

С помощью графиков найдите число решений системы

Пусть (х, ; щ)

х у2 = 21.

Вычислите х1

1 3) з

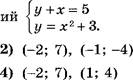
 решение системы уравнений

— у 1 , не решая этой системы.

Решите систему уравнений

ЧАСТЬ 2

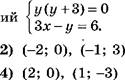
Найдите все значения параметра р, при которых система x2+Y2 = 25 уравнений имеет одно решение.

Ответ:

Составьте систему уравнений для решения задачи: «Площадь прямоугольного треугольника равна 90. Сумма квадратов его катетов — 369. Чему равны длины катетов данного треугольника?»

Ответ:

Вычислите длины катетов по условию задачи 8.

Тест 4                                                                                              4

[Щ Какая пара чисел является решением системы уравне-

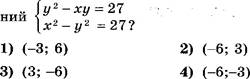
На рисунке изображены графики функций у = (х) и у = g (х). Сколько решений имеет система уравнений

у = g(x)?

-3	-2	y-g(x)

[З С помощью графиков найдите число решений системы

1) (3; 5), (6; -22)

3)                 22), (3; -5) 2) (3; -6), (22; -5)

4)                 (22; -6),          3)

б] Пусть (х] ; щ) — решение системы уравнений х—џ =б х 2 = 42.

Вычислите + Щ, не решая этой системы. 1) 36

Решите систему уравнений

ЧАСТЬ 2

[2 Найдите все значения параметра К, при которых система = 16

уравненийимеет одно решение.

Ответ:

Составьте систему уравнений для решения задачи: «Гипотенуза прямоугольного треугольника равна 68. Площадь его равна 960. Чему равны длины катетов?»

Ответ:

ф] Вычислите длины катетов по условию задачи 8.

Тест 5

1

[2 Какая пара чисел является решением неравенства у! + ху < 5?

[Д На каком рисунке изображено множество точек координатной плоскости, задаваемое неравенством

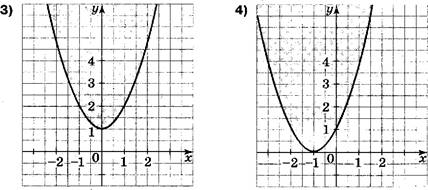
Какая пара чисел является решением системы неравенств

[Д На каком рисунке изображено множество решений системы неравенств

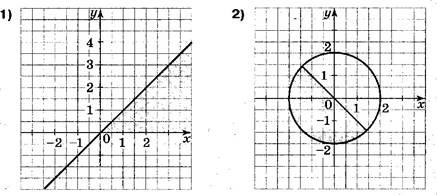
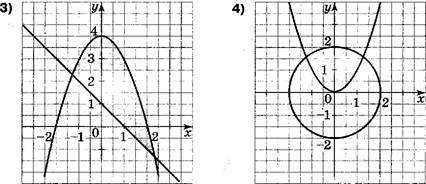
Укажите с множество решений которого изображено на рисунке.

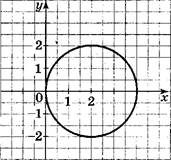
2) 2у-х< 2

Укажите систему двух неравенств с двумя переменными, множество решений которой изображено на рисунке.

ЧАСТЬ 2

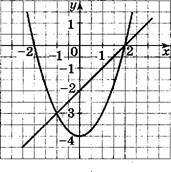
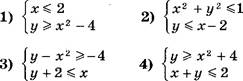
Вычислите площадь фигуры, заданной множеством решений системы неравенств

Найдите наибольшее расстояние между точками этой фигуры.

Ответ:

При каком значении т система неравенств имеет только одно решение?

Ответ:

[ф] Сколько пар натуральных чисел являются решениями системы неравенств

Вычислите сумму всех таких чисел.

Ответ:

42

с

и их системы

Тест 5                                           Вариант 2

ЧАСТЬ 1

Д] Какая пара чисел является решением неравенства

На каком рисунке изображено множество точек координатной плоскости, задаваемое неравенством

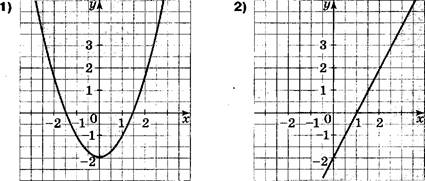
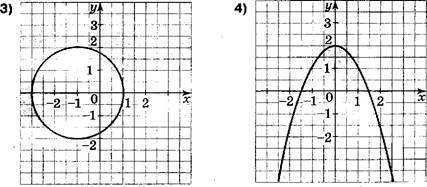
[З Какая пара чисел является решением системы неравенств

Д] На каком рисунке изображено множество решений системы неравенств

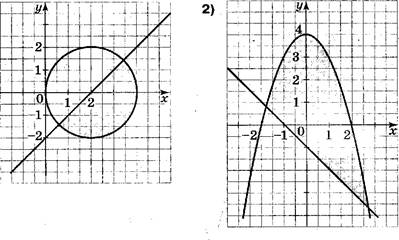
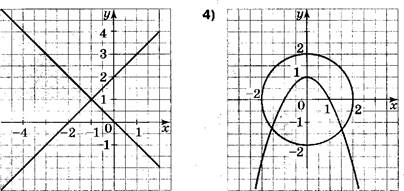
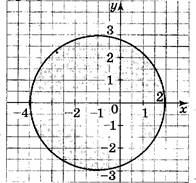
б] Укажите неравенство множество решений которого изображено на рисунке.

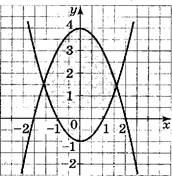
Укажите систему двух неравенств с двумя переменными, множество решений которой изображено на рисунке.

ЧАСТЬ 2

[2 Вычислите площадь фигуры, заданной множеством решений системы неравенств

Найдите наибольшее расстояние между точками этой фигуры.

Ответ:

При каком значении а система неравенств имеет только одно решение?

Ответ:

[0 Сколько пар натуральных чисел являются решениями системы

Вычислите сумму всех таких чисел.

Ответ:

46

и их системы

Тест 5

Вариант З

ЧАСТЬ 1

Д] Какая пара чисел является решением неравенства

[Д На каком рисунке изображено множество точек координатной плоскости, задаваемое неравенством

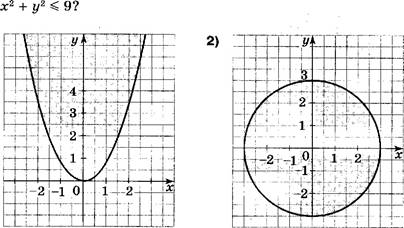
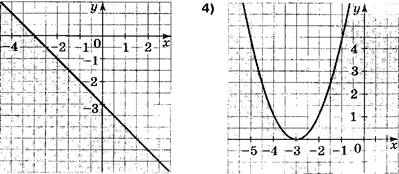
[Щ Какая пара чисел является решением системы нера-

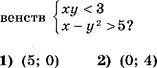
На каком рисунке изображено множество решений системы неравенств

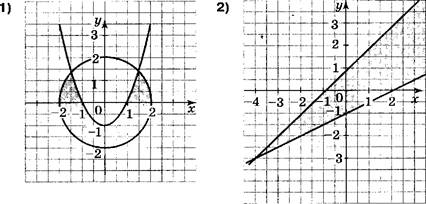
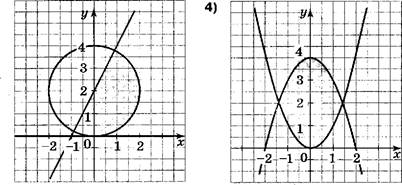
Укажите двумя множество решений которого изображено на рисунке.

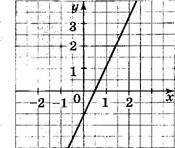
Укажите систему двух неравенств с двумя переменными, множество решений которой изображено на рисунке.

 24

ЧАСТЬ 2

Е] Вычислите площадь фигуры, заданной множеством решений системы неравенств

Найдите наибольшее расстояние между точками этой фигуры.

Ответ:

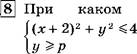значении р система неравенств имеет только одно решение?

Ответ:

Сколько пар натуральных чисел являются решениями системы

Вычислите сумму всех таких чисел.

Ответ:

                                                   50      

двумя и их системы

Тест 5

Вариант 4

ЧАСТЬ 1

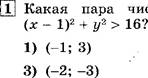Какая пара чисел является решением неравенства

На каком рисунке изображено множество точек координатной плоскости, задаваемое неравенством

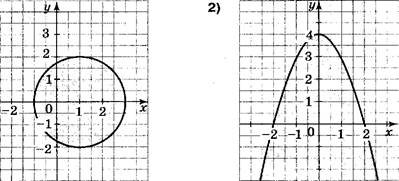
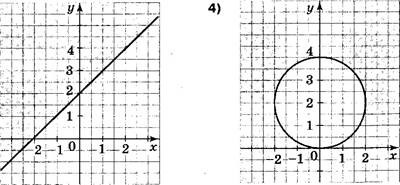
Какая пара чисел является решением системы неравенств

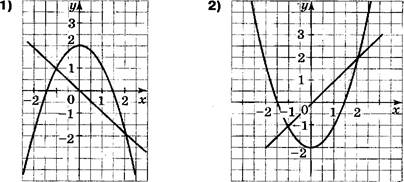
[Д На каком из рисунков изображено множество решений системы неравенств

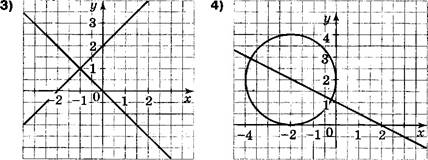
Укажите двумя множество решений которого изображено на рисунке.

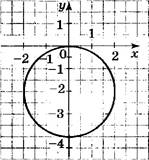
Укажите систему двух неравенств с двумя переменными, множество решений которой изображено на рисунке.

iAV*

Вычислите площадь фигуры, заданной множеством решений системы неравенств

Найдите наибольшее расстояние между точками этой фигуры.

Ответ:

При каком значении Ь система неравенств имеет только одно решение?

Ответ:

Сколько пар натуральных чисел являются решениями системы неравенств

Вычислите сумму всех таких чисел.

Ответ:

Тест 6

1

Д] Какая последовательность чисел является арифметичеСКОЙ прогрессией?

3) 2; 6; 18; 54; 162                    4) 0,3; 0,6; 0,9; 1,2

Найдите первые четыре члена последовательности, заданной формулой хп = 5 — п ² .

[Я Найдите наибольший отрицательный член последовательности ап = 2n — 7.

[З Найдите девятый член арифметической прогрессии -8; -6,5;

Какое число является членом арифметической прогрессии (оп), если а [ = 2, аз = 10?

4) 39

В Вычислите сумму первых двадцати шести членов арифметической прогрессии, заданной формулой ап = 4n — З. 1) 2652       2) 1326

3)      1275

Е]        15 1 пять

Ответ:

В] Сколько отрицательных членов содержится в арифметической прогрессии —32,4; —29,9; 9

Ответ:

Вычислите одиннадцатый член возрастающей арифметической прогрессии, если известно, что а 1 • - — -32

2         4 Ответ:

Тест 6                                                                                               2

Какая последовательность чисел является арифметической прогрессией?

2) з; 6; 12; 24; 48

4)      0,2; 0,6; 1,8; 5,4

[2 Найдите первые четыре члена последовательности, заданной формулой хп = З + 2n ²

                        4) 5; 11; 21; 35

В] Найдите наибольший отрицательный член последовательности а - 5п - 23.

Д] Найдите тринадцатый член арифметической прогрессии —12; —9,5;

                                      4) зо

Какое число не является членом арифметической прогрессии (ал), если а, = З, аз — 11 ?

Вычислите сумму первых десяти членов арифметической прогрессии, заданной формулой ап

З 31 пять

Ответ:

Сколько положительных членов содержится в арифметической прогрессии 12,6; 12,1;

Ответ:

Вычислите двенадцатый член убывающей арифметической прогрессии, если известно, что а 1 + а5 = 8

2   4 Ответ:

Тест 6

З

Какая последовательность чисел является арифметической прогрессией?

[2 Найдите первые четыре члена последовательности (ха), заданной формулой х п = З + п ² .

Найдите наибольший отрицательный член последовательности а = Зп — 8.

Найдите двенадцатый член арифметической прогрессии 26; 23;

б] Какое число является членом арифметической прогрессии (ап), если = 4, а4 = 85? 1) 56

3) 58                                       4) 59

Вычислите девятнадцати членов арифметической прогрессии, заданной формулой а 1) -285

3) -399                                  4) 627

[2                            32 12

ПЯТЬ

Ответ:

В Сколько положительных членов содержится в арифметической прогрессии 18,6; 16,1;

Ответ:

[9] Вычислите пятнадцатый член арифметической прогрессии, если известно, что а 1 • а 4 -32 И а.,2 + - 16.

Ответ:

Тест 6                                                                                                4

Какая последовательность чисел является арифметической прогрессией?

                         1 1 1   1

                        2)

2' 4' 8' 16' 32

Найдите первые четыре члена последовательности, заданной формулой х 2 — па.

   — 14            

Найдите наибольший отрицательный член последовательности 4n — 15.

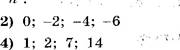
[Д) Найдите тринадцатый член арифметической прогрессии 32; 28;

2) 80

Какое число не является членом арифметической прогрессии (а 1), если а, = 2, а,

4) 52

Вычислите схтмм.у первых двадцати членов арифметической прогрессии, заданной формулой а 1) 1020       

      3) 1090                               4) —880

7 31 пять

Ответ:

Сколько отрицательных членов содержится в арифметической прогрессии —24,1; —22,6;

Ответ:

[О Вычислите десятый член арифметической прогрессии, если известно, что • а 4 —

Ответ:

Тест 7

1

Д] Какая последовательность не является геометрической прогрессией?

1 1

                  4) 4000; 400; 4; 0,4; 0,04

Е] Вычислите пятый        48; 12;	член геометрической	прогрессии
з 1)	1 2)
16 з 3) 4	4

Найдите первый член геометрической прогрессии

2) 1

	4)	1 5
[Д] Вычислите сумму	первых	шести членов	геометриче-

1 1

ской прогрессии

4' 2' з           З 4      4

                   з                                          з

44

Геометрическая прогрессия задана формулой Ь Чему равно отношение : Ь, ?

Сумма четвертого и шестого членов геометрической прогрессии равна 100. Чему равен четвертый член прогрессии, если известно, что ее знаменатель равен 7?

з

   [2                                                      з4'

81

256 •

Ответ:

Первый член возрастающей геометрической прогрессии равен 2. Разность между третьим и вторым членами этой прогрессии равна 12. Найдите ее второй и третий члены.

Ответ:

Найдите все значения х, при которых значения выражениЙ, взятые в указанном порядке: 3х — 5; 2х; 3х, являются тремя последовательными членами геометрической прогрессии.

Ответ:

Д] прогрессией?

1) -56; -44; -32; -20

3) 30; 15; 7,5; 3,75

2

2)

4) 20; 0,2; 0,02; 0,002

Вычислите шестой член геометрической прогрессии

1

4)

                                                                            37         

Найдите второй член геометрической прогрессии Ь, ,

— 18 ; 54 ;

1

9

[Д] Вычислите сумму первых четырех членов геометрической прогрессии 50; —25;

       1) -250                                2) 150

      3) 31,25                              4) 750

Геометрическая прогрессия задана формулой Ь Чему равно отношение : Ь ?

1 3) з

В Разность между седьмым и пятым членами геометрической прогрессии равна 45. Вычислите ее пятый член, если знаменатель прогрессии равен 4.

     Е]                                                      2

5'

16

625'

            Ответ:

Второй член убывающей геометрической прогрессии равен 9. Сумма третьего и четвертого ее членов равна 4. Найдите первый и третий члены прогрессии.

Ответ:

[О Найдите все значения х, при которых значения выражений, взятые в указанном порядке: 5х — 9; 2х; х, являются тремя последовательными членами геометрической прогрессии.

Ответ:

Тест 7

З

[Х не прогрессией?

1 з

Вычислите пятый член геометрической прогрессии

2

      1)                                          2) 1458

27

2

      3)                                          4) 486

81

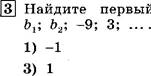Найдите первый член геометрической прогрессии

Д] Вычислите сумму первых шести членов геометрической прогрессии —32; —16;

2) 992

4) 63

[З Геометрическая прогрессия задана формулой Ь Чему равно отношение Ь- : 66?

Сумма третьего и пятого членов геометрической прогрессии равна 450. Чему равен третий член прогрессии, если ее знаменатель равен З?

      1 ) 45      

3) 135

з

2'

81

• 16

Ответ:

Первый член возрастающей геометрической прогрессии равен З. Разность между третьим и вторым членами этой прогрессии равна 6. Найдите ее второй и третий члены.

Ответ:

[О Найдите все значения х, при которых значения выражений, взятые в указанном порядке: х — 6; 2х; 10х, являются тремя последовательными членами геометрической прогрессии.

Ответ:

тест 7

4

прогрессией?

           1) 6; -12; -24; 48                 2) 30; 0,3; 0,03; 0,003        

8' 64

Вычислите шестой член геометрической прогрессии

5; 10;

         1) 320                                 2) 160

               5                                           5

        3)                                           4)

              32                                         64

Найдите второй член геометрической прогрессии

32

1

4)

32

[Д] Вычислите сумму первых четырех членов геометрической прогрессии —24; —8;

5

9

       3) -960                        

Геометрическая прогрессия задана формулой Ь Чему равно отношение : Ь ?

1

1)

5

1

3)

25

Разность между пятым и третьим членами геометрической прогрессии равна 720. Вычислите ее третий член, если знаменатель прогрессии равен 4.

з 1) 16	2) 48
3) 192	з 4)

64

[2                                                     2

32

243'

Ответ:

Второй член возрастающей геометрической прогрессии равен З. Сумма третьего и четвертого ее членов равна 36.  Найдите первый и третий члены прогрессии.

Ответ:

[О Найдите все значения х, при которых значения выражений, взятые в указанном порядке: 3х — 14; 2х; бх, являются тремя последовательными членами геометрической прогрессии.

Ответ:

Тест 8

1

ЧАСТЬ 1

Д] В школьную столовую пришли завтракать девятиклассники. Они должны получить по одному салату и одному стакану сока. Повара предложили ученикам на выбор 4 вида салатов и З вида соков. Сколько всего различных вариантов завтрака может выбрать один ученик?

Вычислите

       1) 600                                 2) 120

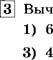Вычислите: — А ²5 .

[Д Из двенадцати рабочих нужно составить бригады по 4 человека в каждой. Сколько существует всевозможных вариантов подбора одной бригады? 1) 520  2) 495

      3) 320                                  4) 135

б] Готовясь к устному экзамену по геометрии, школьник не успел выучить ответ на 4 билета из двадцати. Найдите вероятность того, что на экзамене ученику достался выученный билет.

Все калькуляторы, изготовленные на заводе, проходят обязательную проверку. Из партии в 2000 штук исправными оказались 1910. Вычислите относительную частоту появления неисправных калькуляторов.

191 1)	9 2)
200	100
9 3)	1
200	200

ЧАСТЬ 2

Внутри прямоугольника со сторонами, равными 15 см и 8 см, расположен квадрат со стороной 6 см. Случайным образом отмечается точка внутри прямоугольника. Какова вероятность того, что эта точка будет расположена вне квадрата?

Ответ:

На книжной полке стоит 15 различных книг: 6 из них в твердых переплетах, а остальные в мягких. Ученик берет с полки наугад (с закрытыми глазами) З книги. Какова вероятность того, что все эти книги будут в твердых переплетах?

Ответ:

[Ч Наудачу берется одна кость (фишка) из комплекта для игры в домино. Какова вероятность того, что она содержит число очков не менее 4 и не более 6?

Ответ:

Тест 8

2

ЧАСТЬ 1

[Щ Используя цифры О, 1, З, 5, 7, 9, ученик должен записать все возможные двузначные числа, меньшие 50. Каждая цифра содержится в записи числа только один раз. Сколько таких чисел придется записать ученику?

Вычислите:

1) 210

        3) 60                                    4) 45

8] Вычислите. ⁴7 -С? .

Д] В магазине продают 6 видов булочек. Мальчик решил купить З булочки разных видов. Сколько всевозможных различных вариантов такой покупки он может придумать?

4) 20

На книжной полке в кабинете математики стоят учебники по алгебре: 15 для 9 класса и 10 для 8 класса. Ваня берет наугад одну книжку. Какова вероятность того, что в руках у него будет учебник для 9 класса?

                   2                                                          2

              з                                           5

              З                                            1

              5                                           25

[ф Во время двух баскетбольных матчей 5 игроков одной команды выполнили по 10 штрафных бросков по корзине соперников. Тренер подсчитал, что получилось 8, 7, 9, 9, 7 точных попаданий. Вычислите относительную частоту попадания в корзину одним игроком этой пятерки.

ЧАСТЬ 2

Внутри прямоугольника ABCD со сторонами, равными 15 см и 12 см, изображен прямоугольник MNPK, стороны которого равны 8 см и 5 см. Случайным образом отмечается точка внутри прямоугольника ABCD. Вычислите вероятность того, что она не принадлежит прямоугольнику MNPK.

Ответ:

Сколько всевозможных различных четных пятизначных чисел можно составить из цифр 2, З, 4, 5, 6, 7 (каждая цифра содержится в записи числа только один раз)?

Ответ:

[9] Бросили одновременно два одинаковых игральных кубика. Вычислите вероятность того, что сумма двух открывшихся чисел будет больше или равна 8.

Ответ:

Тест 8

ЧАСТЬ 1

Девятиклассник пришел в библиотеку, чтобы взять домой один сборник стихов и один сборник рассказов. Ему предложили на выбор З различных сборника стихов и 5 различных сборников рассказов. Сколько всевозможных пар книг ученик имеет для выбора?

4) 24 [Ц Вычислите: Рз + Р4.

4) зо

Вычислите: СК —С? .

Ученик составляет всевозможные четырехзначные числа, кратные 5, используя цифры 1, З, 4, 5, 7. Каждая цифра встречается в записи числа только один раз.

Сколько таких чисел должен записать ученик?

       1) 120                                  2) 60

[5 На новогоднем вечере проводилась лотерея. В темный пакет было положено 20 билетов с указанием выигрыша и 5 без выигрыша. Каждый участник вечера берет наугад билет. Миша берет билет первым. Какова вероятность того, что ему достанется билет с выигрышем?

4                                                                                       1

5                                                                                       4

1                                   1

20                                         25

На птицефабрике из 10 ООО куриных яиц в среднем получают 9920 здоровых цыплят. Найдите относительную частоту появления больных цыплят.

            124                                       123

       1)                                          2)

            125                                       124

           1                                  1

3)

            124                                       125

ЧАСТЬ 2

[2 Внутри квадрата со стороной 10 см расположен прямоугольник, стороны которого равны 6 см и 2,5 см. Случайным образом отмечается точка внутри квадрата. Вычислите вероятность того, что эта точка попадет внутрь прямоугольника.

Ответ:

На белых карточках одинакового размера записано по одной букве М, Б, О, Р. Эти карточки выложены на столе в один ряд так, чтобы получилось слово «РОМБ» . Затем все их перевертывают и перемешивают. После этого снова выкладывают карточки в один ряд буквами вверх. Какова вероятность того, что с первого раза вновь получится слово «РОМБ» ?

Ответ:

ф] Сколько всего получится параллелограммов при пересечении четырех параллельных прямых тремя другими параллельными прямыми?

Ответ:

Тест 8

4

ЧАСТЬ 1

[Д Девятиклассник составляет всевозможные четные двузначные числа, используя цифры 1, 2, З, 4, 5. Каждхтк.) цифру он использует в записи числа только один раз. Сколько таких чисел ему придется записать?

         ычислите:      

8!

4) 90

Вычислите: А -

4) 36

Д] Для составления контрольной работы по алгебре учитель подготовил 15 различных заданий примерно одинаковой сложности. Затем он распределил эти задания на карточки по 4 задания на каждой. Карточки отличаются одна от другой хотя бы одним заданием. Сколько всевозможных различных карточек может составить учитель?

2)      265

3)      335       4) 1365

В темный мешок положили З белых и 5 красных шаров одного размера. Мальчик наугад достает из мешка один шар. Какова вероятность того, что он достанет не белый шар?

          з                                             5

5        8 з     1

         8                                           8

На тренировке стрелок выполняет несколько серий выстрелов (по 20 выстрелов в каждой). Записав число точных попаданий в цель в каждой серии, он получил результаты: 18, 17, 19, 16, 19, 15. Какова относительная частота попадания в цель этим стрелком?

            13                                          з

        1)                                     2)

            15                                         10

          1                                  з

        3)                                    4)

            20                                         52

ЧАСТЬ 2

[2 На координатной прямой отмечены точки М (5) и N (25). Между ними отмечается случайным образом некоторая точка Т (х). Найдите вероятность того, что будет справедливо двойное неравенство 8 х 23.

Ответ:

Сколько всевозможных различных пятизначных чисел, кратных 5, можно записать с помощью цифр О, 2, З, 5, 7 (в записи числа каждая цифра содержится только один раз)?

Ответ:

[9 В большом круглом зале 10 одинаковых окон. Какие-то 4 из них не открываются. Найдите вероятность того, что при выборе наугад двух окон удастся открыть хотя бы одно из них.

Ответ:

Тест 9

1

Среди данных чисел найдите наибольшее.

                                4) 3,99

Решите уравнение (х^з + 8) (х^б — З) = О.

[2 целом значении а можно сократить дробь 2х ² + 5х — 3

Найдите все значения Ь, при которых график функции у х ² — 6х — Ь + З имеет две общие точки с осью абсцисс.

4) (6; +00)

ЧАСТЬ 2

1 [О Упростите выражение

Ответ:

[ф Найдите все целые отрицательные числа, которые содержатся в области определения выражения ах +5) (3 — х)

Ответ:

Сумма третьего, четвертого и пятого членов возрастающей арифметической прогрессии равна 9. Произведение второго и шестого ее членов равно —40. Найдите третий член этой прогрессии.

Ответ:

Найдите все значения х, при которых равны значения функций у = х. ^з — 3х и у = З — х. ² .

Ответ:

Два крана, работая вместе, разгрузили баржу за 6 ч. За какое время может разгрузить эту баржу каждый кран, если одному потребуется для этого на 9 ч меньше, чем другому?

Тест 9                                                                       2

[2 Среди данных чисел найдите наименьшее.

з 4)

5

2
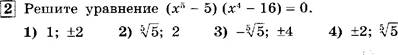
	—4

На рисунке изображен график функции у = ах ² + bx + с. Какому из указанных условий соответствует этот график?

Укажите множество значений функции f (х) —- -3х ² + 18х - 24.

              4) [З; +00)

[2                                        целом значении т можно сократить

4х ² + 3х-1

дробь9

Найдите все значения а, при которых график функции у х!) + 2х + а — 2 не имеет общих точек с осью абсцисс.

3) (З; +00)

ЧАСТЬ 2

[0 Упростите выражение

Ответ:

Найдите все целые положительные числа, которые содержатся в области определения выражения

Ответ:

Разность между первым и третьим членами геометрической прогрессии равна 6. Сумма первого и второго ее членов равна 2. Найдите третий член этой прогрессии.

Ответ:

Найдите все значения х, при которых равны значения выражений х ⁴ — 4х ² и х ² — 4.

Ответ:

Первые 24 км пути мотоциклист проехал за некоторое время. На следующие 36 км он потратил на 15 мин больше, чем на прохождение первой части пути, хотя и увеличил скорость на 4 км/ч. С какой скоростью мотоциклист ехал первую часть пути?

Тест 9

З

Д) Среди данных чисел найдите наибольшее.

2

                                                      4                                                                             

4 2 1
О	1

На рисунке изображен график функции у = ах² + bx + с. Какому из указанных условий соответствует этот график?

1) а > О, с > О 2) а > О, с < О

Укажите множество значений функции f (х) 2х² + 8х + 6. б] Решите систему неравенств

З) (—оо; —1), (1; З) 4) (—оо;

[Ц Для решения системы двух уравнений ученик 9 класса верно построил прямую и парабоЛУ. Какую систему он решал?

2)

4)

Е] целом значении Ь можно сократить дробь 3х ² -5х-2

Найдите все значения р, при которых график функции у = х ² + 4х + р — 5 имеет с осью абсцисс две общие точки.

                      2) (-9; +00)                                  3) (9; +00)

ЧАСТ Ь 2

[Ц] Упростите выражение

36 т 2 т —8 т—

Ответ:

Найдите все целые отрицательные числа, которые содержатся в области определения выражения

Ответ:

Сумма первых пятнадцати членов арифметической прогрессии равна 225. Разность между девятым и третьим ее членами равна 30. Найдите восьмой член этой прогрессии.

Ответ:

Найдите все значения х, при которых равны значения выражений х ^з + 5 и х + 5х ²

Ответ:

Катер, скорость которого в стоячей воде равна 20 км/ч, прошел 22 км по течению реки и 18 км против течения за 2 ч. Найдите скорость течения реки.

Тест 9                                                                       4

[2 Среди данных чисел найдите наименьшее.

2 1) з

[Ц Решите уравнение (х^в — 64) (х⁶ — 6) = О.

4 2 1
о -2	х

В] На рисунке изображен график функции у ах² + bx + с. Какому из указанных условий СООТВетствует этот график?

Д] Укажите множество значений функции f (х) = -2х² - 8х - 4.

2) (—оо; +00)

                               4) [4; +00)        

[2                            целом значении с можно сократить дробь

5х2+9х-2

Найдите все значения т, при которых график функции у = х ² — 4х + т — 1 не имеет с осью абсцисс общих точек.

         3) (5; +00)            

ЧАСТ Ь 2

[9 Упростите выражение

Ответ:

Найдите все целые положительные числа, которые содержатся в области определения выражения

2

Ответ:

Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма четвертого и шестого членов равна 80. Найдите первый член прогрессии.

Ответ:

Найдите все значения х, при которых равны значения функций у = х ⁴ + 7 и у = (3х — 1) (3х + 1).

Ответ:

[$3] Токарь должен обработать 160 деталей к определенному сроку. Обрабатывая в час на 5 деталей больше, чем было намечено по плану, он уже за 1 час до срока обработал на 15 деталей больше. Сколько деталей в час должен обрабатывать токарь по плану?

Тематика тестов

Номер теста	Тема	Время, отводимое на выполнение теста
Тест 1	Функция. Квадратный трехчлен. Квадратичная функция	1 урок
Тест 2	Степенная функция. Корень п-й степени. Целое уравнение и его корни	1 урок
Тест З	Дробные рациональные уравнения. Неравенства с одной переменной	1 урок
Тест 4	Уравнения с двумя переменными и их системы	1 урок
Тест 5	Неравенства с двумя переменными и их системы	1 урок
Тест 6	Арифметическая прогрессия	1 урок
Тест 7	Геометрическая прогрессия	1 урок
Тест 8	Элементы комбинаторики. Начальные сведения из теории вероятностей	1 урок
Тест 9	Итоговый	2 урока

Ответы

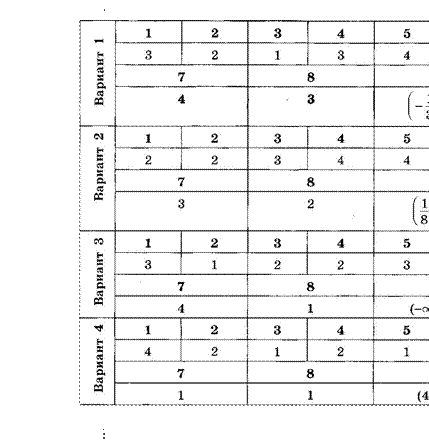
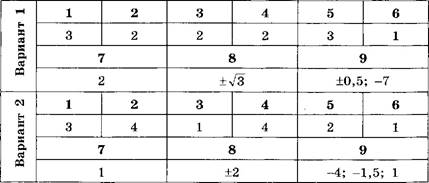
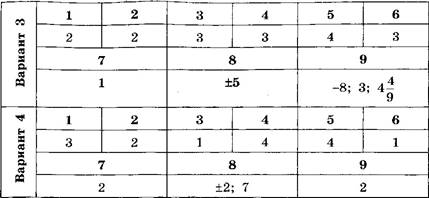
			(—oo; O) U (6; +00)
	-00; -2) U (-2; +00)
			(—oo; O) U (3; +00)
	IJ [3; +00)

Тест 7

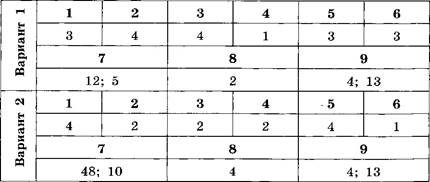
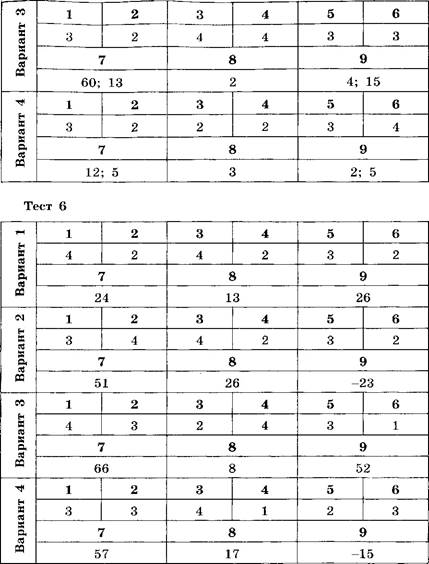
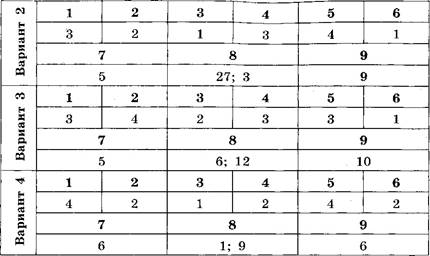
Тест 8

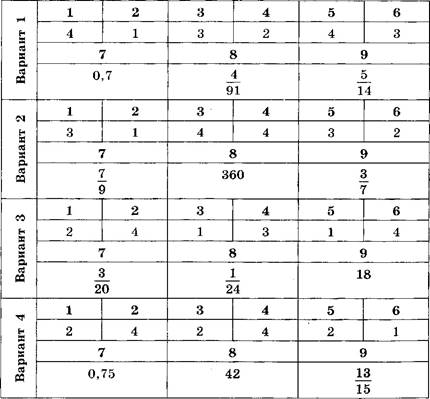
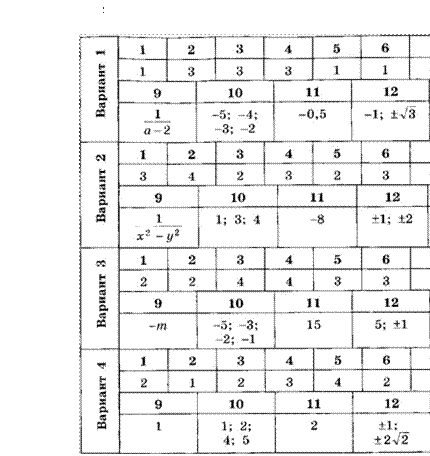
Содержание

Предисловие

Тест 1. Функция. Квадратный трехчлен. Квадратичная функция  7 Вариант 1 .

Вариант 2 .9 Вариант З . .11

Вариант 4 .13

тест 2. Степенная функция. Корень п-й степени.

Целое уравнение и его корни  15

Вариант 1

Вариант 2 .1. 7 Вариант З .19 Вариант 4 .21

Тест З. Дробные рациональные уравнения.

 Неравенства с одной переменной .  23 Вариант 1 .

Вариант 2 .25 Вариант З . .27

Вариант 4 .29

Тест 4. Уравнения с двумя переменными и их системы  31 Вариант 1

Вариант 2 .33

Вариант З .35

Вариант 4 .37

тест 5. Неравенства с двумя переменными и их системы  39 Вариант

Вариант43

Вариант47

Вариант51

94

Тест 6. Арифметическая прогрессия .55

Вариант 1

Вариант 2 .57

Вариант З .59 Вариант 4 .61

Тест 7. Геометрическая прогрессия .63

Вариант 1

Вариант 2 .65

Вариант З .67

Вариант 4 .69

Тест 8. Элементы комбинаторики. Начальные сведения из теории вероятностей71

Вариан т

Вариант73 Вари ан т75 Вариант77

Тест 9.

Итоговый

79

Вариан т

В ари а н т81 В ариан т83

Вариант85

Тематика тестов		87
Ответы		88

Учебное издание

Дудницын Юрий Павлович

Кронгауз Валерий Лазаревич

АЛГЕБРА

Тематические тесты

9 класс

Зав. редакцией Т. А. Бурмистрова

Редактор Н, Б. Грызлова

Младший редактор Е. А. АнДрееикова

Художник О. П. Богомолова Художественный редактор О. П. Богомолова

Компьютерная графика А. Г. Вьюниковской

Технический редактор и верстальщик Н. К. Румянцева

Корректоры М. А. Терентьева, Л. С. АлењсанДрова

Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000. изд. лиц. Серия ИД 05824 от 12.09.01.

Лодписано в печать 16.05.11. Формат 60 х 90 ¹ /16. Бумага газетная. Гарнитура Школьная. Печать офсетная. Уч.-изд. л. З, 19. Тираж 5 ООО экз. Заказ .N2 31751.

Открытое акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.

Отпечатано в ОАО «Саратовский полиграфкомбинат» .

410004, г. Саратов, ул. Чернышевского, 59. www.sarpk.ru