ТЕСТ ПО АЛГЕБРЕ, 9 класс
Тема: «Квадратичная функция»
Цель контроль за усвоением знаний, умений, навыков учащихся по теме
Уровень сложности базовый
Время на выполнение одного тестового задания 60 минут
Инструкция по выполнению работы
На выполнение работы дается 1 час (60 минут). Работа содержит 30 заданий на одну тему с выбором ответа (один верный ответ из четырех предложенных). С помощью заданий с выбором ответа проверяется базовый уровень подготовки по теме.
В бланке теста отмечать правильный ответ или делать какие-либо пометки запрещено. Выбранный ответ необходимо отметить на отдельном бланке ответов.
Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднения, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.
За выполнение заданий дается один балл. Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
1. Квадратичной функцией является
1) y = 2x-4 2) y
= 4x – x[1] 3) y = x2 5x 4) y = x62 .
|
1) 6 2) -6 3) 8 7. Произведение нулей функции у = x(6-x) |
4) -8. |
|
1) 6 2) [2][3] 3) -1 8. Вершина параболы y = (x-2)2+5 |
4) -[4]. |
|
1) (-2;5) 2) (2;5) 3) (-2;-5) |
4) (2;-5) |
9. Знаки коэффициентов a, b, с для параболы, изображенной на рисунке
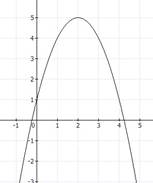
1)a<0, b>0, c>0 2)a>0, b>0, c<0 3)a<0, b<0, c>0 4)a>0, b<0,c>0.
10. Наибольшее значение функции y = -x2+ 4x
1) -4 2) -12 3) 0 4) 4.
11. Наименьшее значение функции y = (x-5)2-6
1) -6 2) 5 3) -11 4) -5.
12. Точка, лежащая на параболе y = -x2+3x-[5]
1) A(-1;1) 2) (1;1) 3) (2;9) 4) (-2;-[6]).
13. Значение а, при котором график функции y = a-2x+x2 проходит через точку С(-[7], 5)
1) [8] 2) -4 3) 2 4) -1.
14. Значение р, при котором вершина параболы y = x2-px+6 в точке
(2; 4)
1) 3 2) -4 3) 2 4) -1.
15. Функция, изображенная на рисунке возрастает на интервале
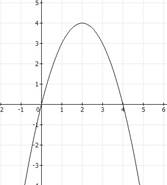
1) (2;+) 2) [2;+) 3) (-;2] 4) [0;4].
16. Наибольшее значение функции
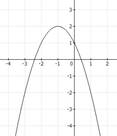
1) -2 2) 2 3) -[9] 4) 1.
17. Промежуток убывания функции, изображенной на рисунке
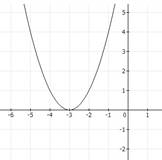
1) (-3;+) 2) [-3;+) 3) (-;-3] 4) [-3,5;0,5].
18. Абсциссы точек пересечения графиков функций y = -2x2+3x-5 и y = -5
1) -1,5;0 2) 2;-3 3) 0;1,5 4) -1;-2.
19. Абсциссы точек пересечения графиков функций y = x2-16 и y =
-x2+4
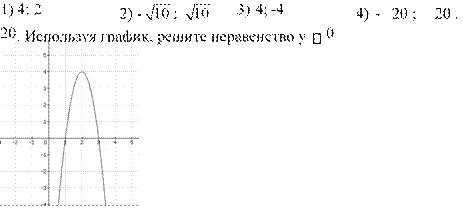
21. Используя графики функций y = x2+2x-2 и y = x, решите неравенство x2+2x-2 х
1) (-2;1) 2) [1;+) 3) (-;-2] 4) [-2;1].
22. График функции у = (х – 2)2 изображен на рисунке
1. 2. 3. 4.
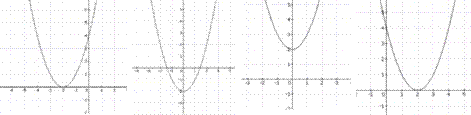
1) 4 2) 3 3) 1 4) 2.
23. Значение а, при котором абсцисса вершины параболы у = ах2-4х+5 равна 6
1) 3 2) -3 1 4) 1,5.
3)
3 24. Парабола у = 4х-2х2+5 симметрична относительно прямой
1) х = -2 2) х = 0,5 3) х = 1 4) х = 0,25.
25. Вершина параболы лежит на оси ординат, если
1) у = х2-4 2) у = (х – 3)2 3) у = х2-4х+4 4) у =х2+3х.
26. Промежуток убывания функции у = -х2+3х
1) [-3;+) 2) [1,5;+) 3) (-;-1,5] 4) (1,5;+)
27. Уравнение функции, график которой симметричен графику функции у = х2-2х относительно прямой у =0
1) у = х2+2х 2) у = (х – 1)2 3) у = -х2+2х+1 4) у =2х-х2.
|
№ п/п |
Ответ |
№ п/п |
Ответ |
|
1. |
2 |
16. |
2 |
|
2. |
2 |
17. |
3 |
|
3. |
3 |
18. |
3 |
|
4. |
3 |
19. |
2 |
|
5. |
2 |
20. |
4 |
|
6. |
2 |
21. |
4 |
|
7. |
1 |
22. |
4 |
|
8. |
2 |
23. |
3 |
|
9. |
3 |
24. |
3 |
|
10. |
4 |
25. |
1 |
|
11. |
1 |
26. |
2 |
|
12. |
2 |
27. |
4 |
|
13. |
3 |
28. |
1 |
|
14. |
1 |
29. |
3 |
|
15. |
3 |
30. |
1 |
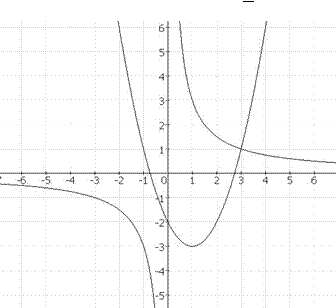
28.
Решение неравенства х2-2х-2 > 3 Инструкция по проверке тестовых заданий x За каждое верно выполненное задание
учащийся получает 1 балл. Максимальное количество баллов – 30. Оценка
определяется исходя из следующих показателей:
- от 25 до 30 баллов – оценка «5»
- от 19 до 24 баллов – оценка «4»
- от 12 до 17 балла – оценка «3»
- 11 и менее баллов – оценка «2»
Бланк ответов
1) (-;0) 2) (3;+) 3) (-;3) 4) (0;+).
(3;+)
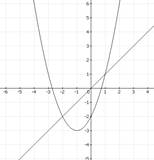
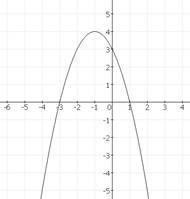
29. Функция, график которой изображен на рисунке, задается формулой
1) у =- х2+х-3 2) у = х2+2х-3 3) у = -х2-2х+3 4) у =-х2+2х-3.
30. Используя графические представления, решите неравенство (х – 4)2 0
1) х = 4 2) любое число 3) нет решений 4) [-2;2].
[1] . Абсцисса вершины параболы y = -2x2+4x-6
[2] ) (0;3) 2) (3;0) 3) (0;9) 4) (9;0).
[3] . Парабола y = x2+4x+3 пересекает ось абсцисс в точках 1) (0;3), (0;-1) 2) (-3;0), (-1;0) 3) (0;1), (0;3) 4) (3;0),(1;0).
[4] . Сумма нулей функции y = x2+6x+8
[5] ) -1 2) 1 3) -2 4) 2.
[6] . Ордината вершины параболы y = 6x-x2
[7] ) 6 2) 0 3) 9 4) 3.
[8] . Координаты точки пересечения графика y = 9- x2 с осью ординат
[9] ) (-;1][3;+) 2) [0;4] 3) [2; +) 4) [1;3].
ТЕСТ ПО АЛГЕБРЕ, 9 класс
Наименьшее значение функции y = (x-5) 2 -6 1) -6 2) 5 3) -11 4) -5
Используя графики функций y = x 2 +2x-2 и y = x, решите неравенство x 2 +2x-2 х 1) (-2;1) 2) [1;+ )…
Решение неравенства х 2 -2х-2 > 3
Используя графические представления, решите неравенство (х – 4) 2 0 1) х = 4 2) любое число 3) нет решений 4) [-2;2]
![Используя графические представления, решите неравенство (х – 4) 2 0 1) х = 4 2) любое число 3) нет решений 4) [-2;2]](https://fs.znanio.ru/d5af0e/5f/cc/8717b6739a7224cf2b6504ffd047215880.jpg)
© ООО «Знанио»
С вами с 2009 года.
