Тест по теме "Тригонометрические уравнения"

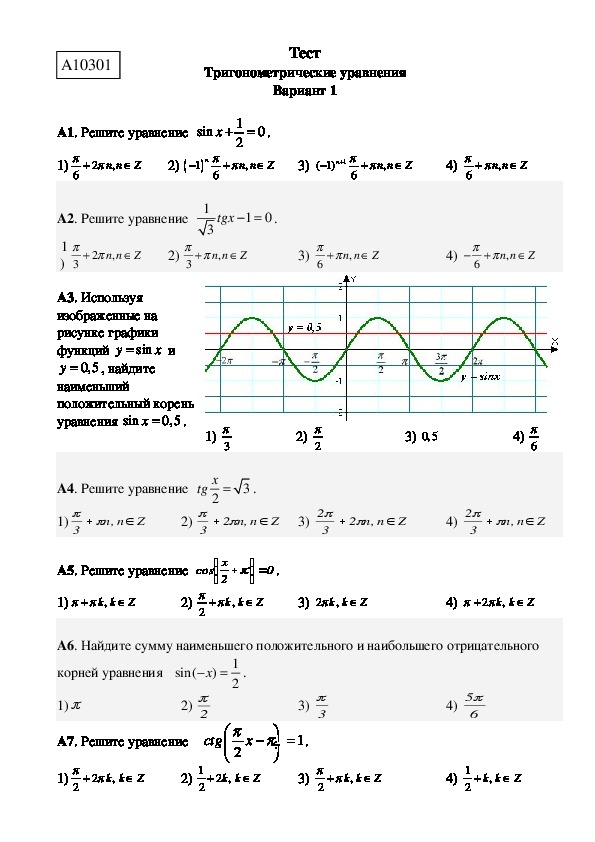
А10301 Тест Тригонометрические уравнения Вариант 1 А1. Решите уравнение   sin 1)   2 6 , n n Z  2)   1 n 1 x   . 0 2    , n n Z 6  А2. Решите уравнение   tgx   . 1 0  1 )   2 3 , n n Z  2) , n n Z  1 3   3 3) n  1  ( 1)    6 , n n Z  3)   6 , n n Z  4) 4)   6 , n n Z     6 , n n Z  y А3. Используя  изображенные на  рисунке графики  sin x функций  y  , найдите  наименьший  положительный корень  уравнения sin 0,5 x  0,5  и  . 1)                    2)  3                        3)  0,5                     4)  2  6 А4. Решите уравнение   1)  3  Zn,n  2) А5. Решите уравнение   1)   ,k k Z  2) 3 . x 2   tg   3 Zn,n2  3)  2 3   Zn,n2  4)  2 3  Zn,n  .    x   cos 0 2      2 , k k Z 3) 2   ,k k Z 4)   2 ,k k Z  А6. Найдите сумму наименьшего положительного и наибольшего отрицательного  корней уравнения    sin( 1) 2) x  2 ) 1  . 2 3)  3 4) 5 6 А7. Решите уравнение     ctg 1)   2 2 , k k Z  2) 1 2  2 , k k Z      2 x  1 . 3)   2 , k k Z  4) 1 2  , k k Z     x   . А8. Решите уравнение     2 3 cos 3 0 7   7 14 , n n Z 6    7 7 1 6  2) , n n Z 1)       n 3)   n    7  1 6 , n n Z  4)    7 2 6  , n n Z  А9. Выберите число, являющееся корнем уравнения  1) 1 6  6 2) 3) 4 3  2sin    3 x  2  3 . 4)  5 6 А10. Выберите число, которое не является корнем уравнения  3 1)  2 3 3)   5 6 2) 1 3   1 . tg 4)    x  2 4  3 Дополнительное задание: решить уравнение:    2 ) sin а  ) в tgx  sin х 12 ctgx 2 0;   х   1 0. б ) 1 7 cos  2 x  3sin 2 ; x        