Топографические карты, планы и чертежи.

Тема 1 Топографические карты, планы и чертежи.

1.1   Общие сведения о картах, планах и чертежах.

Вопросы темы:

1.     Задачи геодезии, форма и размеры Земли. Математическая модель Земли. Понятия « геодезия», « основная уровенная поверхность», «геоид», «земной сфероид».

2.     Понятия «географическая карта», «топографическая карта» «план местности».

3.     Определение положения точек земной поверхности, системы географических и прямоугольных координат.

4.     Высоты точек. Превышения. Балтийская система высот.

5.     Изображение земной поверхности на плоскости, метод ортогонального проектирования.

Основные термины и понятия :

1.     Геоид

2.     Земной сфероид

3.     Географическая карта

4.     Топографическая карта

5.     План местности

6.     Система координат

7.     Широта, долгота точки

8.     Условная и основная уровенные поверхности

9.     Абсолютная и относительная высоты точек

10. Превышение

11. Горизонтальное проложение

Вопрос 1 Задачи геодезии, форма и размеры Земли. Понятия « геодезия», « основная уровенная поверхность», «геоид», «земной сфероид».

Геодезия – слово греческого происхождения, образовано из двух греческих слов ge (гео) земля и daizo (дайдзо) разделяю, что в переводеозначает землеразделение. Такое буквальное определение геодезии говорит только лишь о том, что она является одной из древнейших наук о Земле. Возникла эта наука с началом земледелия. В процессе исторического развития содержание каждой науки непрерывно меняется, в связи с чем неизбежен разрыв между названием науки и её содержанием. Так, например, геометрия буквально определяется как землеизмерение.

Однако в наше время измерения на Земле не являются предметом геометрии. Данной проблемой занимается геодезия – наука об измерениях на земной поверхности и в околоземном пространстве, а также о вычислениях и графических построениях, проводимых:

-          для определения фигуры и размеров Земли как планеты в целом;

-          исследования движения земной коры;

-          изображения земной поверхности и отдельных её частей в виде планов, карт и профилей (вертикальных разрезов);

-          решения разнообразных научных и практических задач по созданию и эксплуатации искусственных сооружений на земной поверхности и в околоземном пространстве;

-          создания геодезических опорных сетей как основы для выполнения вышеперечисленных задач.

Таким образом, предметом геодезии является геометрическое изучение физической поверхности Земли и происходящих с ней изменений.

Поверхность Земли  характеризуется многообразием форм. На

ней находятся всевозможные объекты естественного и искусственного

происхождения, геометрическое моделирование которых имеет для человека исключительно важное значение.

Проектирование, строительство и эксплуатация инженерных сооружений, планировка, озеленение и благоустройство населенных мест, изучение и добыча полезных ископаемых, сельскохозяйственное и лесное производство, обеспечение обороноспособности государств – во всех этих и многих других сферах жизнедеятельности человека приходится решать задачи геометрического характера, связанные с поверхностью Земли. Их решение основывается на методе измерения различных величин. Данный метод является неотъемлемой частью геодезии. В геодезии широко используют достижения астрономии, физики, математики, механики, электроники, геоморфологии и других наук.

В процессе своего развития геодезия разделилась на ряд научных дисциплин: высшую геодезию, топографию, инженерную геодезию, картографию, фотограмметрию, радиогеодезию, космическую геодезию,геодезическое инструментоведение и др.

Высшая геодезия изучает форму и размеры Земли, движение её коры и определяет:

-          вид и размеры Земли (как планеты);

-          внешнее гравитационное поле Земли (значение и направление силы тяжести в земном пространстве и на поверхности);

-          взаимное расположение значительно удалённых друг от друга геодезических пунктов;

-          точность изображения пунктов на плоскости в проекции с учётом

-          искажений из-за кривизны земной поверхности.

Топография изучает методы изображения участков земной поверхности по материалам съёмочных работ и создания на их основе топографических карт и планов.

Инженерная геодезия изучает методы и способы геодезического обеспечения при разработке проектов, строительстве и эксплуатации разнообразных сооружений, а также при освоении и охране природных ресурсов.

Космическая геодезия рассматривает теорию и методы решения научных и практических задач на земной поверхности по наблюдениям небесных тел (Луна, Солнце, ИСЗ) и по наблюдениям Земли из космоса. Космическая геодезия включает в себя глобальные навигационные системы, являющиеся основой применяемых в настоящее время координатных систем,и системы космического дистанционного зондирования многоцелевого назначения, используемые для мониторинга поверхности Земли.

Предметом изучения картографии являются методы и способы отображения поверхности Земли и протекающих на ней процессов в видеразличных образно-знаковых моделей, в том числе цифровых и электронных карт.

Фотограмметрия решает задачи измерений по аэрофото- и космическим снимкам для различных целей: создания карт и планов, проектирования и строительства сооружений, обмеров и определения площадей застроек, лесных массивов и т. п.

В геодезии для обозначения формы земной поверхности используют термин «фигура Земли».

Знание фигуры и размеров Земли необходимо во многих областях и прежде всего для определения положения объектов на земной поверхности и правильного её изображения в виде карт, планов и цифровых моделей местности.

Физическая поверхность Земли состоит из подводной (70,8 %) и надводной (29,2 %) частей. Подводная поверхность включает в себя систему срединно-океанических хребтов, подводные вулканы, океанические желоба, подводные каньоны, океанические плато и абиссальные равнины. Надводная часть земной поверхности также характеризуется многообразием форм. С течением времени поверхность Земли из-за тектонических процессов и эрозии постоянно изменяется. Представление о фигуре Земли (рис. 2) в целом можно получить, вообразив, что вся планета ограничена мысленно продолженной поверхностью океанов в спокойном состоянии.

Уровенных поверхностей, огибающих Землю, можно вообразить множество. Та из них, что совпадает со средним уровнем воды океанов в спокойном состоянии, т. е. в момент полного равновесия всей массы находящейся в ней воды под влиянием силы тяжести, называется основной уровенной поверхностью Земли.

В геодезии, как и в любой другой науке, одним из основополагающих принципов является принцип перехода от общего к частному. Исходя из него, для решения научных и инженерных задач по изучению физической поверхности Земли, а также других геодезических задач, сначала необходимо определиться с математической моделью поверхности Земли.

Математическая поверхность Земли.

Рассмотрим любое тело в виде материальной точки А на физической поверхности Земли (рис. 1).

На точку А оказывают влияние две силы: сила притяжения FП, направленная к центру Земли, и центробежная сила вращения Земли вокруг своей оси FЦ, направленная от оси вращения по перпендикуляру.Равнодействующая этих сил называется силой тяжести FТ.

 

 

 

 

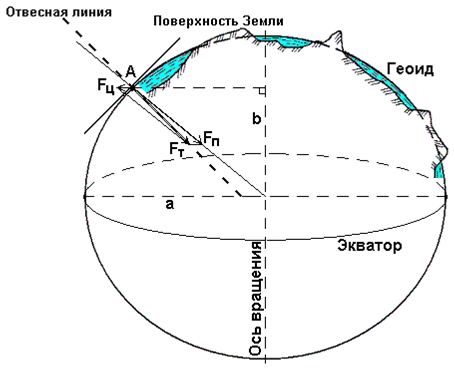
Рис. 1. Геоид – уровенная поверхность Земли

В любой точке земной поверхности направление силы тяжести, называемое ещё вертикальной или отвесной линией, можно легко и просто определить с помощью уровня или отвеса. Оно играет очень большую роль в геодезии. По направлению силы тяжести ориентируется одна из осей пространственной системы координат.

Если через точку А построить замкнутую поверхность, которая в каждой своей точке будет перпендикулярна отвесной линии (направлению силы тяжести), то данную поверхность можно принять в качестве математической при решении некоторых частных задач в геодезии. Такая поверхность получила название уровенной или горизонтальной. Её недостаток в том, что она содержит элемент неопределенности, т. е. через любую точку можно провести свою уровенную поверхность, и таких поверхностей будет бесчисленное множество. Для устранения этой неопределенности при решении общих геодезических задач принимается так называемая общая математическая поверхность, т. е. уровенная поверхность, которая в каждой своей точке совпадает со средним уровнем морей и океанов в момент полного равновесия всей массы воды под влиянием силы тяжести. Такая поверхность носит название общей фигуры Земли или поверхности геоида.

Геоид – выпуклая замкнутая поверхность, совпадающая с поверхностью воды в морях и океанах в спокойном состоянии и перпендикулярная к направлению силы тяжести в любой её точке (см. рис. 1).Из-за неравномерного распределения масс внутри Земли геоид не имеет правильной геометрической формы, и в математическом отношении его поверхность характеризуется слишком большой сложностью. Поэтому там, где это допустимо, поверхность геоида заменяется приближенными математическими моделями, в качестве которых принимается в одних случаях земной сфероид, в других – земной шар, а при топографическом изучении незначительных по размеру территорий – горизонтальная плоскость, т. е. плоскость, перпендикулярная к вертикальной линии в данной точке.

Земной сфероид – эллипсоид вращения, который получается вращением эллипса вокруг его малой оси b (см. рис. 1), совпадающей с осью вращения Земли, причем центр эллипсоида совмещается с центром Земли. Размеры эллипсоида подбирают при условии наилучшего совпадения поверхности эллипсоида и геоида в целом (общеземной эллипсоид) или отдельных его частей (референц-эллипсоид). Фигура референц-эллипсоида наилучшим образом подходит для территории отдельной страны или нескольких стран. Как правило, референц-эллипсоиды принимают для обработки геодезических измерений законодательно.

Наиболее удачная математическая модель Земли в виде референц-эллипсоида была предложена проф. Ф. Н. Красовским с большой полуосью a = 6378245 м, малой – b = 6356863 м и коэффициентом сжатия у полюсов a = (a-b)/a = 1/298.3 ~ 1/300.

Постановлением Совета Министров СССР № 760 от 7 апреля 1946 года эллипсоид Красовского принят для территории нашей страны в качестве математической поверхности Земли.

В инженерной геодезии для практических расчетов за математическую поверхность Земли принимают шар со средним радиусом R = 6371.11 км. Объем шара равен объему земного эллипсоида.

Вопрос 2 Понятия «географическая карта», «топографическая карта» «план местности».

Географические карты — это уменьшенное изображение земного шара, построенное в картографической проекции.

Топографическая карта — географическая карта универсального назначения, на которой подробно изображена местность. Топографическая карта содержит сведения об опорных геодезических пунктах, рельефе, гидрографии, растительности, грунтах, хозяйственных и культурных объектах, дорогах, коммуникациях, границах и других объектах местности. (ru.wikipedia.org›Топографическая_карта)
Топографической картой называется уменьшенное, подробное и точное изображение небольшого участка местности на плоскости (бумаге).
Топографическая карта - основной графический документ о местности, содержащей точное, подробное и наглядное изображение местных предметов и рельефа.

План местности — разновидность топографической карты; чертёж небольшого участка местности в крупном масштабе. Планы применяются туристами, коммунальными и аварийными службами, в сельском хозяйстве и в других местах, где нужно ориентироваться на местности и изучать участки. (ru.wikipedia.org›Топографическая_карта)

 

Вопрос 3 Определение положения точек земной поверхности, системы географических и прямоугольных координат

 

Система координат – это система величин, определяющих положение точки в пространстве или на плоскости.

Наибольшее распространение в геодезии получили: географическая система координат, полярная система координат, плоская прямоугольная система координат, зональная система координат.

Географическая система координат

Географическими координатами называются угловые величины -  широта и долгота, которые определяют положение точки на земном шаре.

Широта точки – это угол, составленный отвесной линией, проходящей через эту точку, и плоскостью экватора. Счет широт ведется от плоскости экватора к северу и югу до 90º. Северная широта положительная, южная – отрицательная.

Долгота точки – это двугранный угол, между плоскостями начального меридиана и меридиана, проходящего через данную точку земной поверхности. Счет долгот ведется от начального (Гринвического) меридиана к востоку и западу на 180º. Восточная долгота положительная,  западная – отрицательная.

Географические координаты определяются по результатам астрономических наблюдений, а выражаются в градусах, минутах и секундах.

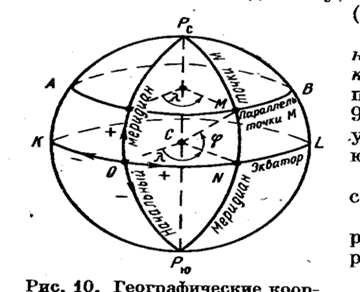
Рис.2 Географические координаты

Географические координаты:

λ – долгота точки М, восточная, положительная, до 180 º

φ – широта точки М, северная, положительная, до 90 º.

На рис.2 Рс и Рю – Северный и Южный полюса Земли, линия Рс Рю – ось вращения Земли. Плоскости КОNL – плоскость экватора, плоскость АМВ, параллельна экватору, - параллель, а плоскости, проходящие через ось Земли – меридианы.

Через каждую точку земной поверхности можно провести только один меридиан и одну параллель.

Плоская прямоугольная система координат

В отличии от географической системы, координаты которой измеряются в градусах, плоская прямоугольная система координат характеризуется линейными величинами – абсциссой и ординатой, определяющими положение точки на плоскости.

Систему этих координат представляют две взаимно перпендикулярные линии, именуемые осями координат. Точка их пересечения (О) называется началом координат.

Ось ординат совпадает с направлением пояса и называется осью игреков, а ось абсцисс совпадает с направлением меридиана и называется осью иксов, что полностью отличает данную систему от такой же системы применяемой в математике.

В системе плоских прямоугольных координат положение точки относительно начала координат О определяется кратчайшим расстоянием до осей абсцисс и ординат.

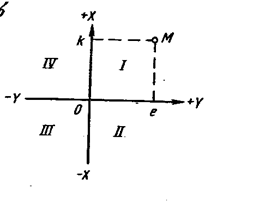
Рис.3 Плоская прямоугольная система координат.

Отрезок ОК называют абсциссой, а Ое – ординатой точки М. обозначаются эти отрезки соответственно Х и У и выражаются в метрах.

Оси координат разделяют плоскости чертежа на четыре четверти, нумерация которых, в отличие от такой же системы координат в математике, ведется по часовой стрелке. В первой четверти координаты Х и У положительны, во второй - Х отрицательный, а У – Положительный, в третьей четверти обе координаты отрицательные, в четвертой - Х положительный, У отрицательный.

Это можно записать следующим образом:

Абсциссы точек вверх от оси ординат положительны, а вниз от нее отрицательны;

Ординаты точек вправо от оси абсцисс положительны а лево от нее отрицательны.

Знаки координат по четвертям сведены в таблицу.

 

Четверти	Координаты
	Х	У
І северо - восток (СВ)	+	+
І І юго – восток (ЮВ)	-	+
І І І юго - запад (ЮЗ)	-	-
ІV северо – запад (СЗ)	+	-

 

 

Вопрос 4 Высоты точек. Превышения. Балтийская система высот.

При изображении земной поверхности на плоскости в виде плана или карты при проектировании и строительстве инженерных сооружений крайне важно иметь представление о неровностях земной поверхности, о том, насколько одна точка располагается выше или ниже другой.

Через каждую точку на поверхности Земли можно провести уровенную поверхность. При небольших расстояниях между точками можно считать, что уровенные поверхности параллельны между собой (рис. 4).

Высотой точки принято называть отрезок отвесной линии от этой точки до условной уровенной поверхности, принятой за начало отсчета высот.

В случае если высота точки определяется относительно основной уровенной поверхности, то такие высоты называют абсолютными.

Абсолютными высотами точек ,,,являются соответственно длины отрезков ,,,. Точки, размещенные на одной уровенной поверхности (точки и на рис. 4), имеют одинаковые высоты. Абсолютные высоты обозначают преимущественно буквой .

За основную уровенную поверхность принята поверхность, которая проходит через нуль Кронштадтского футштока (рис. 4). Футшток представляет собой медную пластину, закрепленную в устое моста через обводной канал в ᴦ. Кронштадте. Нанесенная на пластине горизонтальная черта соответствует среднему уровню воды в Балтийском море, наблюдения за которым ведутся с 1825 года. По этой причине система высот принято называть Балтийской.

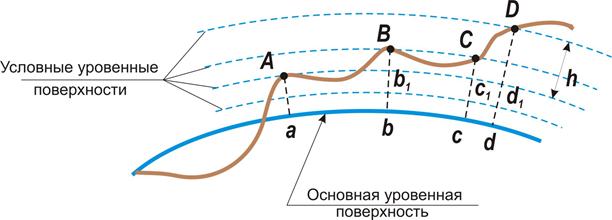
Рис. 4 Абсолютные и относительные высоты

За начало отсчета высот может быть принята любая уровенная поверхность, к примеру, уровенная поверхность, которая проходит через точку .

Высоты, вычисленные относительно некоторой условной поверхности, называются условными или относительными.

Условная высота точки равна нулю, точек и равна отрезкам и , а точки - .

Высота одной точки относительно уровенной поверхности другой точки принято называть относительной высотой или превышением этих точек. Таким образом, превышение равно разнице абсолютных или относительных высот двух точек. Для точек и можно записать

(1)

В случае если известна высота точки и измеренное превышение между точками и , то высота точки определяется по формуле

(2)

Системы высот

Третьей координатой, определяющей положение точки в пространстве, является её высота. В геодезии для определения отметок точек применяются следующие системы высот (рис. 5): ортометрическая (абсолютная); геодезическая; нормальная (обобщенная); относительная (условная).

Рис.5 Системы высот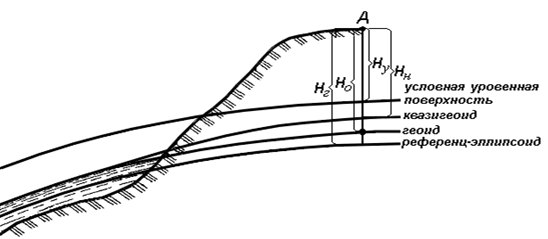

Ортометрическая (абсолютная) высота Hо – расстояние, отсчитываемое по направлению отвесной линии от поверхности геоида до данной точки.

Геодезическая высота Hг – расстояние, отсчитываемое по направлению нормали от поверхности референц-эллипсоида до данной точки.

В нормальной системе высот отметка точки Hн отсчитывается по направлению отвесной линии от поверхности квазигеоида, близкой к поверхности геоида.

Квазигеоид («якобы геоид») – фигура, предложенная в 1950-х гг. советским учёным М.С. Молоденским в качестве строгого решения задачи определения фигуры Земли. Квазигеоид определяется по измеренным значениям потенциалов силы тяжести согласно положениям теории М.С. Молоденского.

В нашей стране все высоты реперов государственной нивелирной сети определены в нормальной системе высот. Это связано с тем, что положение геоида под материками определить сложно. Поэтому с конца 40-х годов в СССР было принято решение не применять ортометрическую систему высот.

В России абсолютные высоты точек определяются в Балтийской системе высот (БСВ) относительно нуля Кронштадтского футштока –

горизонтальной черты на медной пластине, прикрепленной к устою моста через обводной канал в г. Кронштадте.

Относительная высота Hу – измеряется от любой другой поверхности, а не от основной уровенной поверхности.

Местная система высот – Тихоокеанская, её уровенная поверхность ниже нуля Кронштадтского футштока на 1873 мм.

 

Вопрос 5 Изображение земной поверхности на плоскости, метод ортогонального проектирования.

Поверхность Земли изображают на плоскости в виде планов, карт, профилей. При составлении планов сферическую поверхность Земли проецируют на горизонтальную плоскость и полученное изображение уменьшают до требуемого размера. Как правило, в геодезии применяют метод ортогонального проецирования. Сущность его состоит в том, что точки местности переносят на горизонтальную плоскость по отвесным линиям, параллельным друг другу и перпендикулярным горизонтальной плоскости.

Например, точка А местности (перекресток дорог) проецируется на горизонтальную плоскость Н по отвесной линии Аа, точка В – по линии Вb и т.д., точки а и b являются ортогональными проекциями точек А и В местности на плоскости Н. Полученное на плоскости изображение участка земной поверхности уменьшают с сохранением подобия фигур. Такое уменьшенное изображение  как называется? (план местности). Следовательно, мы можем дать еще одно определение плана местности – это уменьшенное подобное изображение горизонтальной проекции участка поверхности Земли с находящимися на ней объектами.

Однако план нельзя составить на очень большую территорию, так как сферическая поверхность Земли не может быть развернута в плоскость без складок или разрывов. Изображение Земли на плоскости, уменьшенное и искаженное вследствие кривизны поверхности,  как называют? (карта).
Таким образом, и план, и карта – это уменьшенные изображения земной поверхности на плоскости.

Различие между ними состоит в том, что при составлении карты проецирование производят с искажениями поверхности за счет влияния кривизны Земли, на плане изображение получают практически без искажения.

При ортогональной проекции линии проектирования перпендикулярны плоскости проекции. Проведем через точки A, B, C, D линии, перпендикулярные плоскости проекции P; в пересечении их с плоскостью P получим ортогональные проекции a, b, c, d соответствующих точек (рис.5) .

 

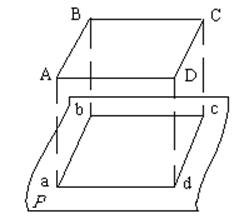
Рис.6 Ортогональная проекция

 

Горизонтальное проложение.

При изображении физической поверхности Земли на карте (плоскости) ее вначале проектируют отвесными линиями на уровенную поверхность (рис.7), а затем уже по определенным правилам это изображение развертывают на плоскость.

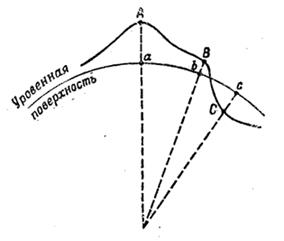
Рис.7 Проектирование физической поверхности Земли на уровенную поверхность.

При изображении небольшого участка земной поверхности соответствующий участок уровенной поверхности принимают за горизонтальную плоскость и, спроектировав на нее этот участок, получают топографический план местности.

Геометрическая сущность такого изображения заключается в следующем. Если из каждой точки какой-нибудь прямой АВ (рис.8), произвольно расположенной в пространстве, опустить перпендикуляр на горизонтальную плоскость Р (плоскость проекций), то точки пересечения перпендикуляров с плоскостью составят прямую ab, которая и будет плановым изображением прямой АВ. Изображение в плане точек и линий земной поверхности называется их горизонтальным проложением или горизонтальной проекцией.

В том случае, когда проектируемая линия горизонтальна, ее изображение в плане равно длине самой линии. Если проектируемая прямая наклонна, то ее горизонтальное проложение всегда короче ее длины и уменьшается с увеличением угла наклона. Горизонтальное проложение вертикальной линии представляет точку.

Рис.8 Горизонтальное проложение (изображение в плане) точки, прямой, ломаной и кривой линий.

При создании карты на нее наносят в заданном масштабе, то есть с определенным уменьшением, горизонтальные проложения всех точек местности, линий, контуров, проектируя их на уроненную поверхность Земли, которую в пределах листа карты принимают за горизонтальную плоскость. На местности все линии обычно наклонны, а, значит, их горизонтальные проложения всегда короче самих линий.

Горизонтальное проложение наклонной линии

Для составления плана необходимо знать горизонтальные проложения линий местности. Если измеренная на местности линия АВ имеет длину D (рисунок 9) и не горизонтальна, а имеет угол наклона υ, то горизонтальная проекция этой линии d = АС определится по формуле

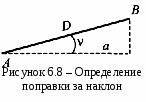d = D cos υ.

 

 

 

 

Рис.9 Определение поправки на наклон

Место горизонтальной проекции линии d на практике часто вычисляют разность ΔD=D–d, которую называют поправкой за наклон линии:

ΔD = D – D cos υ = 2D sin² υ/2. (3)

По формуле (3) составлены таблицы, из которых по аргументам D и υ находится поправка за наклон линии ΔD. Эту поправку необходимо всегда вычитать из D, чтобы получить d.

При обычных измерениях линии лентой поправки за наклон линии учитываются при углах наклона υ ≥ 2^о. Для углов наклона меньше 2^о поправки за наклон сравнительно малы (находятся в пределах точности измерения линий) и поэтому ими можно пренебречь.

Если измеряемая линия местности имеет в разных своих частях различные углы наклона, то поправки за наклон вычисляются для каждой части отдельно. В этом случае поправка для всей линии будет равна сумме поправок ее частей.

Вопросы для самоконтроля

 

1. Что такое геодезия и какие вопросы она решает?

2. Что такое уровенная поверхность Земли?

3. Что такое геоид?

4. Каковы размеры эллипсоида Ф.Н. Красовского?

5. Что называется широтой и долготой?

6. Какие системы координат применяются в геодезии?

7. В чем заключается суть системы прямоугольных координат?

8. Что называется абсолютной и условной высотой точки?

9. В чем заключается ортогональная проекция линии?

10. Дайте определение понятиям «географическая карта», « топографическая карта», «план местности», «превышение», «горизонтальное проложение».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru