Виды тригонометрических неравенств

Тригонометрическими неравенствами называются неравенства, содержащие переменную в аргументе тригонометрической функции. 

            cos x a< , cos x a≤ , cos x a> , cos x a≥ ;

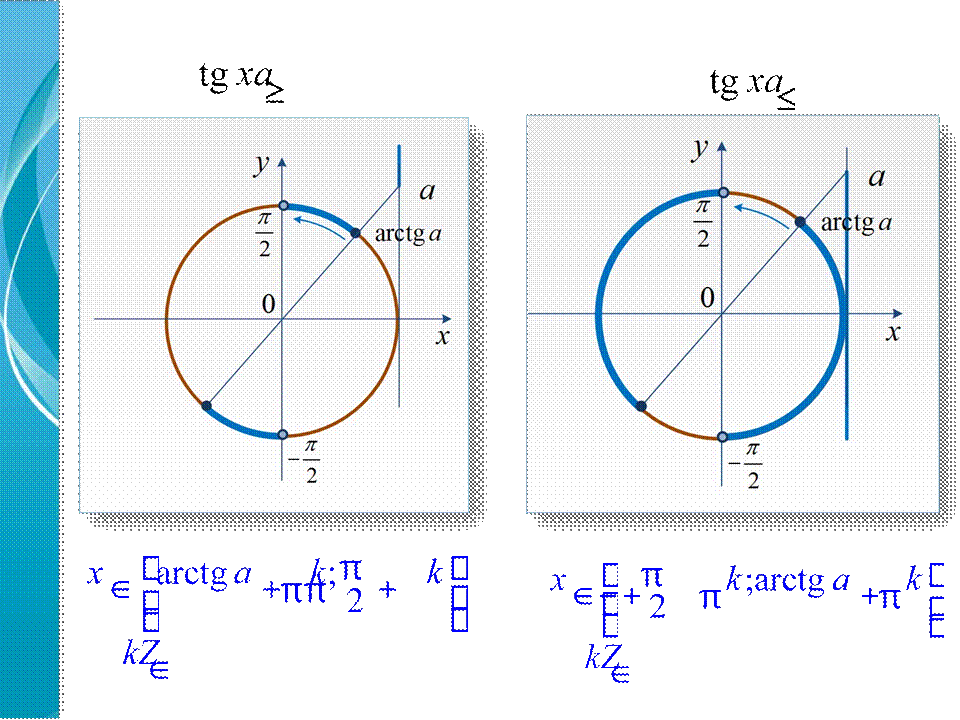
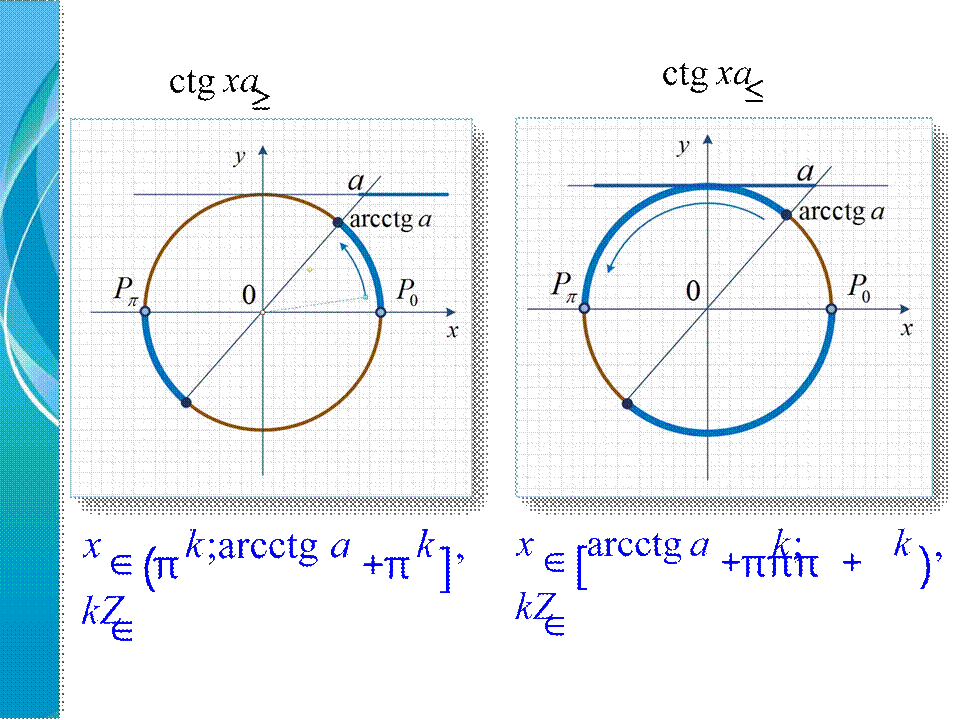
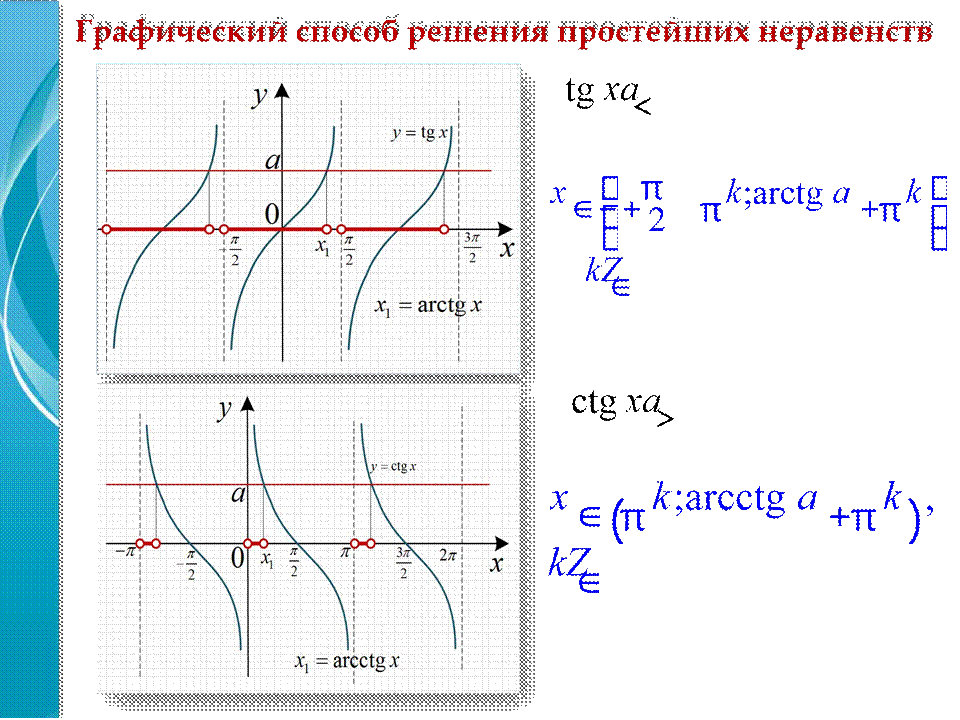
     tg x a< , tg x a≤ , tg x a> , tg x a≥ ;   ctg x a< , ctg x a≤ , ctg x a> , ctg x a≥ ;

Способы решения этих неравенств совершенно очевидным образом вытекают из представления тригонометрических функций на единичном круге. 

sin x a≤

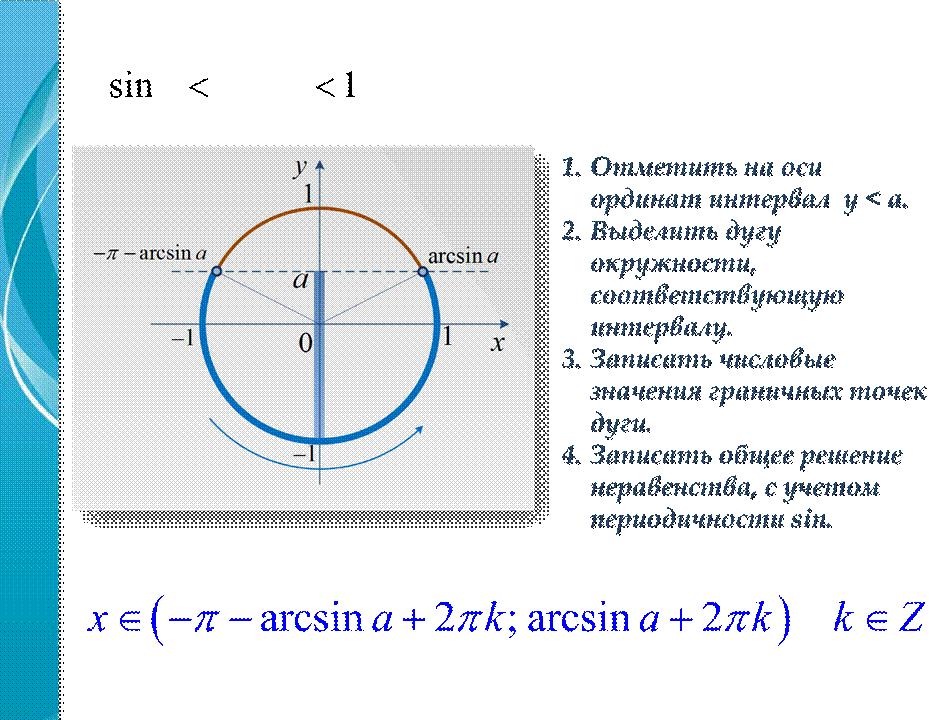
Если a ≤1, то − −_π arcsina+ 2πn x≤ ≤ arcsina+ 2πn n, ∈¢

Если a>1, то x любое действительноечисло x−  ( ∈¡)

Если a<−1, то решений нет

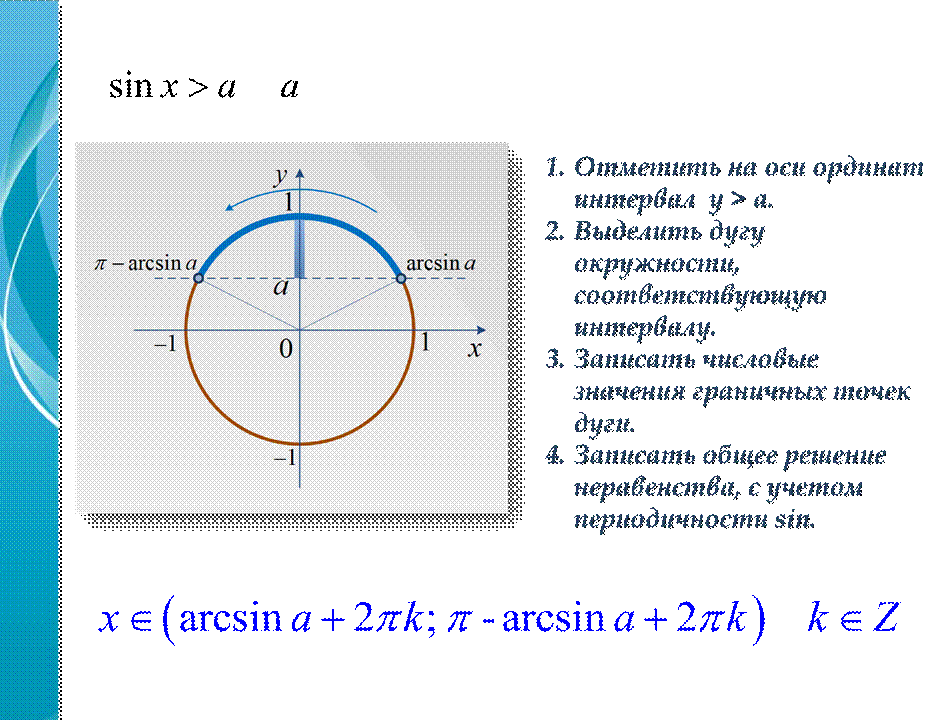
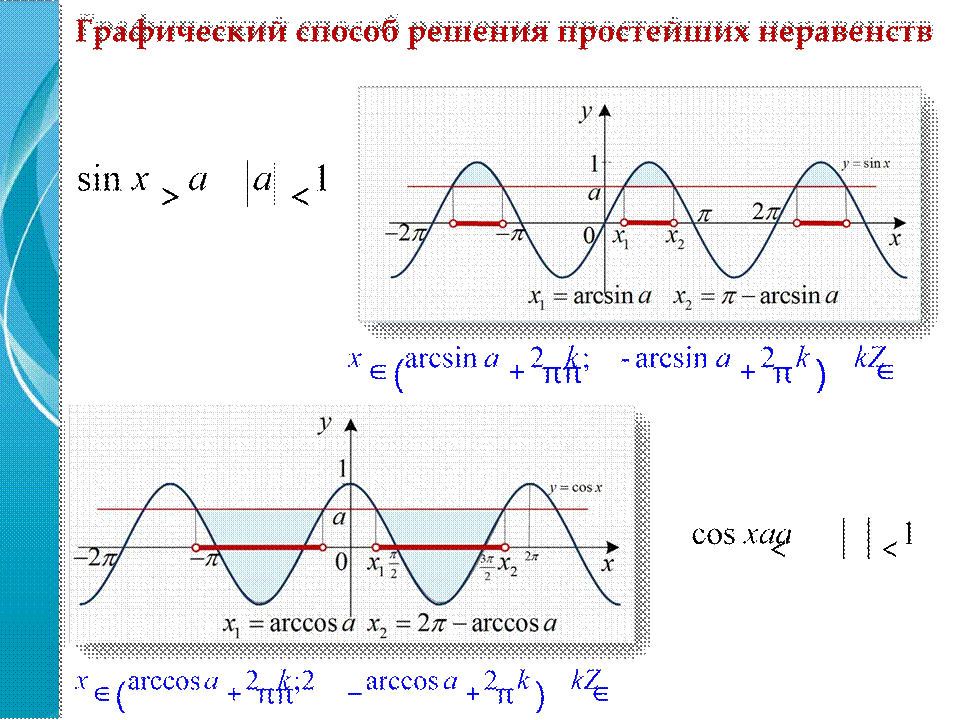
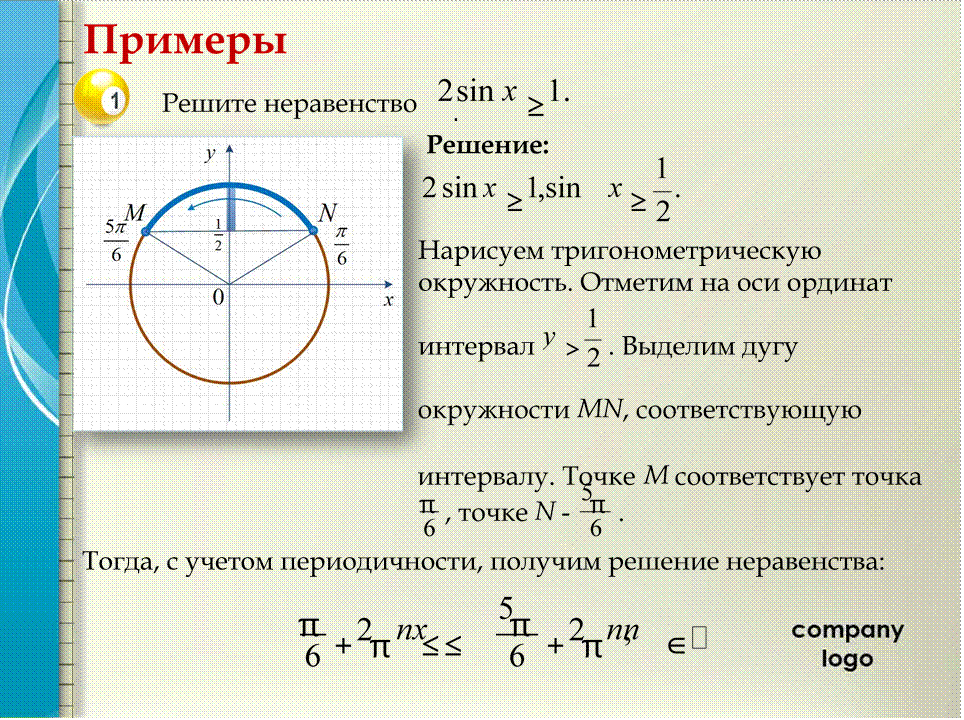
sin x a≥

Если a ≤1, то arcsina+ 2πn x≤ ≤ −_π arcsina+ 2πn n, ∈¢

Если a>1, то решений нетто

Если a<− −1, x любое действительноечисло x( ∈¡)

cos x a≤

Если a <1, то arccosa+ 2πn x≤ ≤ −2_π arccosa+ 2πn n, ∈¢

Если a>1, то x любое действительноечисло x−  ( ∈¡)

Если a<−1, то решений нет

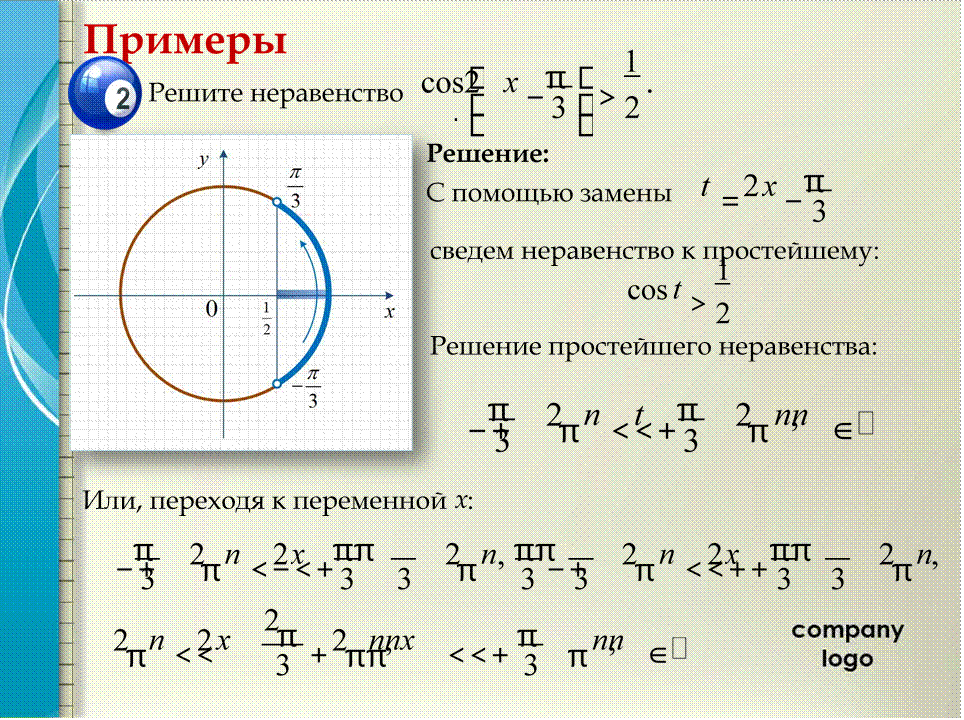
cos x a≥

Если a <1, то −arccosa+ 2πn x≤ ≤−arccosa+ 2πn n, ∈¢

Если a>1, то решений нет

Если a<−1, то x любое действительноечисло x− ( ∈¡)

Список используемой литературы

1.        Алгебра в таблицах. 7-11 кл.: Справочное пособие/Авт.сост. Л.И.Звавич, А.Р.                  Рязановский. 4-е изд., стереотип – М.: Дрофа, 2000. 

2.        Бородуля И.Т. Тригонометрические уравнения и неравенства: Кн. для учителя. – М.:    Просвещение, 1989. 

3.        Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: Кн. для учащихся. – М.: Просвещение, 1988.

4.        Крамор В.С., Михайлов П.А Тригонометрические функции: (Система упражнений для самостоят. изучения).

Пособие для учащихся. 2-е изд., доп. – М.: Просвещение, 1983.