
Тема: «Тригонометрические тождества.».
Часть 2. Установите, истинны или ложны следующие утверждения. (« да» или «нет»).
Вариант 1.
1. Значение
косинуса не может быть больше ![]() .
.
2. Значение
тангенса не может быть больше ![]() .
.
3. Основное тригонометрическое тождество имеет вид: sin ɑ + cos ɑ = 1
4. tg
ɑ = ![]() .
.
5. Косинус угла ɑ не может принимать значения по модулю превышающие 1.
6. Тангенс угла ɑ не может принимать значения по модулю превышающие 1.
7. sin
2 ![]() + cos 2
+ cos 2 ![]() = 1/
= 1/
8. sin
2 ![]() =
= ![]()
![]()
9. Если sin ɑ= - 0,6 и 1,5π <ɑ< 2π, то cos ɑ= 0,8.
10. Если sin
ɑ=
- 0,6 и 1,5π <ɑ<
2π, то ctg ɑ
= ![]() .
.
11. Тангенсом угла ɑ называется отношение синуса этого угла к его косинусу.
12. Ctg
ɑ = ![]() .
.
13. Если ctg ɑ = 5, то tg ɑ= 0,2 .
14. Если tg
ɑ
= ![]() ,
то cos ɑ
= ± 0,5
,
то cos ɑ
= ± 0,5
15. Если 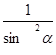 =17
,
то ctg ɑ =± 4
=17
,
то ctg ɑ =± 4
16. 1+ tg
2 ɑ = 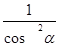
Часть 2. Установите, истинны или ложны следующие утверждения. (« да» или «нет»).
Вариант 2.
1
Значение
синуса не может быть ![]() .
.
2. Значение тангенса не
может быть больше ![]() .
.
3.Основное тригонометрическое тождество имеет вид: sin2 ɑ + cos 2ɑ = 1
4. ctg
ɑ = ![]() .
.
5. Косинус или синус угла ɑ не может принимать значения по модулю превышающие 1.
6. Котангенс угла ɑ не может принимать значения по модулю превышающие 1.
7. sin
2 ![]() + cos 2
+ cos 2 ![]() = 1.
= 1.
8. sin
2 ![]() =
= ![]()
![]()
9. Если cos ɑ= - 0,8 и π <ɑ< 1,5π, то sin ɑ= 0,6.
10. Если sin ɑ= - 0,6 и 1,5π <ɑ< 2π, то tg ɑ = - 0,75 .
11. Котангенсом угла ɑ называется отношение синуса этого угла к его косинусу.
12. tg
ɑ = ![]() .
.
13. Если tg ɑ =0,5, то сtg ɑ= 2 .
14. Если сtg
ɑ
= ![]() ,
то cоs
ɑ
= ± 0,5
,
то cоs
ɑ
= ± 0,5
15. Если 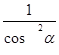 =10
,
то tg ɑ =± 3
=10
,
то tg ɑ =± 3
16. 1+ ctg
2 ɑ = 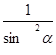
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.