
Тригонометрические уравнения профильного уровня из материалов ЕГЭ.
Справочный материал.
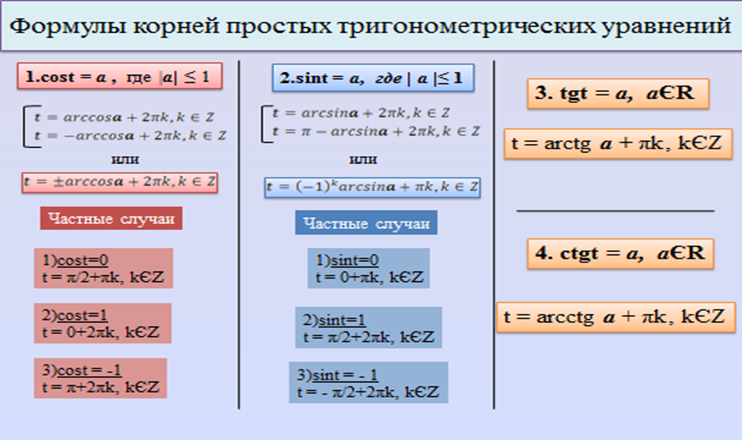
Часть 1. Использование основных тригонометрических формул.
Пример 1.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. 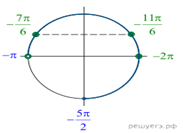 а) Преобразуем
обе части уравнения:
а) Преобразуем
обе части уравнения:
![]()
![]()
![]()
откуда ![]() или
или ![]()
Из уравнения ![]() находим:
находим: ![]() где
где ![]()
Из уравнения ![]() находим:
находим:
![]() где
где
![]()
б) С помощью числовой окружности отберём корни,
принадлежащие промежутку ![]() Получим
числа:
Получим
числа: ![]()
![]()
![]()
Ответ: а) ![]()
![]()
![]()
![]() б)
б) ![]()
![]()
![]()
Пример 2. Дано
уравнение ![]()
а) Решите данное уравнение.
б) Укажите корни данного уравнения,
принадлежащие промежутку ![]()
Решение.  а) Сведем
уравнение к квадратному относительно тангенса:
а) Сведем
уравнение к квадратному относительно тангенса:
![]()
![]()
![]()
![]()
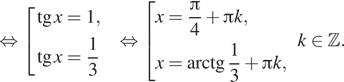
б) С помощью числовой окружности находим, что
из найденных решений промежутку принадлежат числа ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 3.
. а) Решите уравнение ![]()
б) Укажите корни этого уравнения,
принадлежащего отрезку ![]()
Решение. 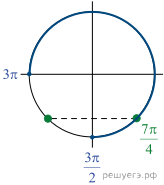 а) Запишем
исходное уравнение в виде:
а) Запишем
исходное уравнение в виде:
![]()
![]()
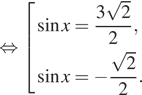
Уравнение ![]() корней
не имеет. Значит,
корней
не имеет. Значит, 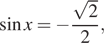 откуда
откуда
![]() или
или
![]()
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку ![]() Получим
число
Получим
число ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 4.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Пусть ![]() тогда
тогда
![]() откуда
откуда ![]() или
или
![]()
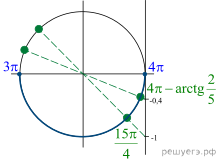
Имеем два уравнения:
![]()
![]()
б) С помощью числовой окружности выберем корни
уравнения на промежутке ![]() Получим
числа:
Получим
числа: ![]()
Ответ: a)![]() б)
б)![]()
![]()
21. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение:
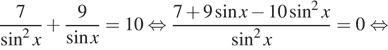
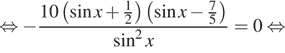
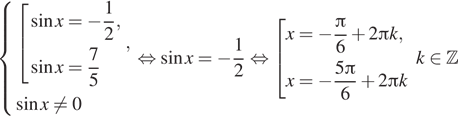
б) 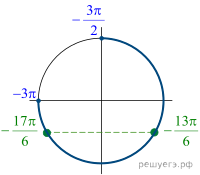 С
помощью числовой окружности отберём корни, принадлежащие отрезку
С
помощью числовой окружности отберём корни, принадлежащие отрезку ![]()
Получим числа ![]()
Ответ: а) ![]()
![]() где
где
![]() б)
б) ![]()
Пример 5.
Решите уравнение ![]() б) Укажите
корни уравнения, принадлежащие отрезку
б) Укажите
корни уравнения, принадлежащие отрезку ![]()
Решение. а) Преобразуем уравнение, получаем ![]() Значит,
Значит, ![]() или
или ![]() где
где
![]() В первом случае
В первом случае ![]() во
втором случае
во
втором случае ![]() где
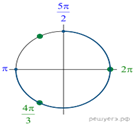
где ![]() Первая серия решений входит во вторую. б) Отметим
решения на тригонометрической окружности. Отрезку
Первая серия решений входит во вторую. б) Отметим
решения на тригонометрической окружности. Отрезку ![]() принадлежат
корни
принадлежат
корни ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 6.
а) Решите уравнение ![]()
б) Найдите решения уравнения, принадлежащие отрезку [3; 5].
Решение. а) Возведем обе части уравнения в квадрат:
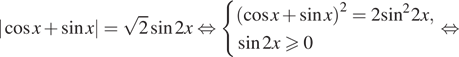
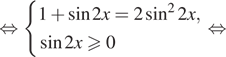
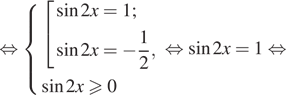
![]()
б) Если ![]() то
то ![]() поэтому
при таких k решений на отрезке [3; 5] нет.
поэтому
при таких k решений на отрезке [3; 5] нет.
Если ![]() то
то ![]() Заметим,
что
Заметим,
что ![]() поэтому
корень
поэтому
корень ![]() лежит на
отрезке [3; 5].
лежит на
отрезке [3; 5].
Если ![]() то
то ![]() поэтому
при таких k решений на отрезке [3; 5] нет.
поэтому
при таких k решений на отрезке [3; 5] нет.
Ответ: ![]()
![]()
Пример 7.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. а) Используя формулу ![]() заменим
выражение в скобках на
заменим
выражение в скобках на ![]() получаем
однородное тригонометрическое уравнение первой степени:
получаем
однородное тригонометрическое уравнение первой степени:
![]()
Если ![]() то из
уравнения следует
то из
уравнения следует ![]() что невозможно
в силу основного тригонометрического тождества. Значит, на множестве корней
уравнения
что невозможно
в силу основного тригонометрического тождества. Значит, на множестве корней
уравнения ![]() Разделим
обе части уравнения на
Разделим
обе части уравнения на ![]()
![]()
б) Составим двойное неравенство: ![]() откуда
откуда
![]() Следовательно,
Следовательно,
![]() Поэтому на данном отрезке получаем единственный корень
Поэтому на данном отрезке получаем единственный корень ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 8.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Заметим, что ![]() Преобразуем
уравнение:
Преобразуем
уравнение:
![]()
![]()
![]()
![]()
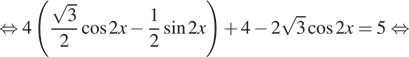
![]()
![]()
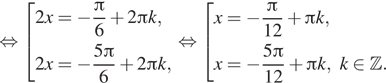
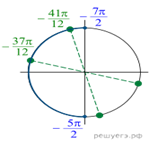
б) С помощью числовой окружности
(см. рис.) отберём корни, принадлежащие отрезку ![]() Получим
числа
Получим
числа ![]() Ответ:
а)
Ответ:
а) ![]()
![]() где
где
![]() б)
б) ![]() Ответ
в пункте а) можно записать и в другой форме. Например,
Ответ
в пункте а) можно записать и в другой форме. Например, ![]()
![]() где
где
![]()
Пример 9.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 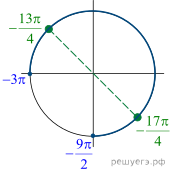 а) Применим
формулу приведения, понизим порядок уравнения, используем формулу косинуса
суммы. Получаем:
а) Применим
формулу приведения, понизим порядок уравнения, используем формулу косинуса
суммы. Получаем:
![]()
![]()
![]()
![]()

![]()
![]()
![]()
б) Корни, принадлежащие заданному отрезку,
отберем при помощи тригонометрической окружности. Получим числа ![]() Ответ:
а)
Ответ:
а) ![]() где
где
![]() б)
б) ![]()
Пример 10. а) Решите
уравнение: ![]()
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
Решение. 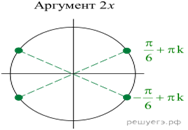
а) Воспользуемся формулой ![]() Из
неё следует, что
Из
неё следует, что ![]() Поэтому
из исходного уравнения получаем:
Поэтому
из исходного уравнения получаем:
![]()
![]()
![]()
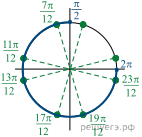
б) При помощи тригонометрической окружности отберём корни, принадлежащие заданному отрезку.
Получим ![]()
Ответ: а) ![]() б)
б)
![]()
б) При помощи тригонометрической окружности отберём корни, принадлежащие заданному отрезку.
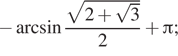
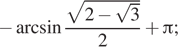
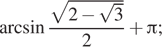
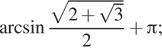

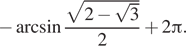
Ответ: a) 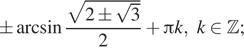
б) 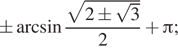
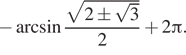
Ответ: а) ![]() б)
б)
![]() a)
a)
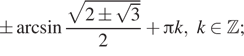
б) 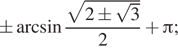
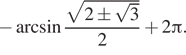
Пример 11. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем левую часть уравнения при помощи формулы разности косинусов:
![]()
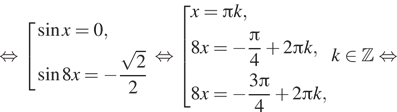
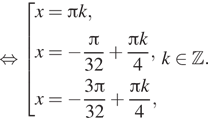
б) Отберём корни, принадлежащие отрезку ![]() Учитывая,
что
Учитывая,
что ![]() решим
неравенства:
решим
неравенства:
|
Значит, |
Значит, |
Значит, |
На указанном промежутке лежат числа ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 12.а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. a) Преобразуем уравнение:
![]()
![]()
![]()
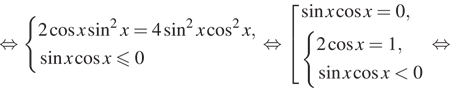
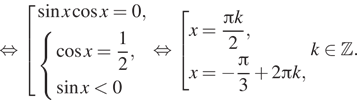
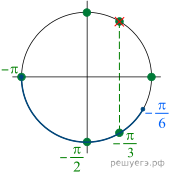
б) При помощи единичной окружности отберём
корни, лежащие на заданном отрезке (см. рис.). В него попадают числа ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 13.
а) Решите уравнение 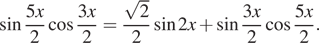
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
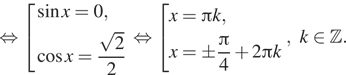
Решение. а) Преобразуем уравнение:
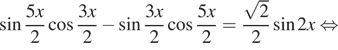
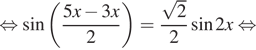
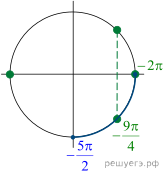
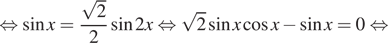
![]()
б) Отберем корни при помощи единичной
окружности, найдём: ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
Пример 14.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Используем формулу синуса двойного угла и перегруппируем выражения:
![]()
![]()
![]()
![]()
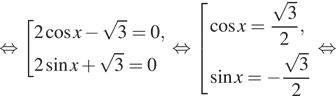
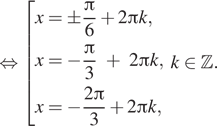
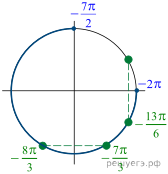
б) Отберем корни при помощи единичной
окружности. Нам подходят ![]()
Ответ: а)![]()
б) ![]()
Пример 15..
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Знаменатель дроби не может быть равен нулю:
![]()
![]()
При таких х можно умножить на знаменатель, а значит,
исходное уравнение эквивалентно уравнению ![]() откуда
откуда
![]() и,
следовательно,
и,
следовательно,
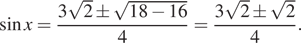
Тогда
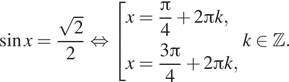
Ограничению удовлетворяет только ![]()
б) Найденные решения соответствуют точке
единичной окружности, лежащей во второй четверти. Поэтому никакое из решений не
лежит на отрезке ![]()
Ответ: а) ![]() б)
искомых решений нет.
б)
искомых решений нет.
Пример 16. а) Решите
уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. a) Сгруппируем слагаемые и разложим левую часть уравнения на множители:
![]()
![]()
![]()
![]()
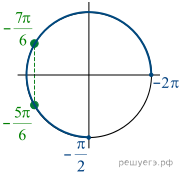
б) С помощью числовой окружности отберём корни
уравнения, принадлежащие отрезку ![]() Получим
числа
Получим
числа ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 17.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Применим формулу синуса двойного угла, получим в правой части уравнения
![]()
Перенесем выражение из правой части в левую, применим
формулу ![]()
![]()
![]()
![]()
Теперь заметим, что
![]()
и разложим на множители:
![]()
![]()
Далее имеем: 
![]()
или
![]()
![]()
![]()
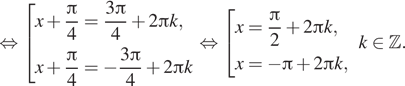
б) Отберем корни при помощи единичной
окружности (см. рис.). На заданном отрезке лежат корни ![]() и
и ![]()
Ответ: а)![]() б)
б) ![]() ;
; ![]()
Пример 18.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 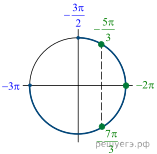 а) Обозначим
а) Обозначим
![]() тогда
уравнение примет вид
тогда
уравнение примет вид ![]() откуда t = 1 или
t = 2. Далее имеем:
откуда t = 1 или
t = 2. Далее имеем:
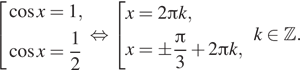
б) Корни отберем с помощью тригонометрической
окружности (см. рис.). На отрезке ![]() лежат
числа
лежат
числа ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 19.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. 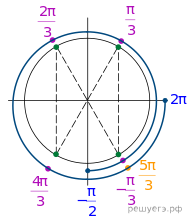 а) Преобразуем
уравнение:
а) Преобразуем
уравнение:
![]()
![]()
![]()
![]()
б) Отберём корни при помощи тригонометрической
окружности (см. рис.). На заданном промежутке лежат корни: ![]()
![]()
![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
![]()
![]()
Пример 20. а) Решите уравнение
![]()
![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. 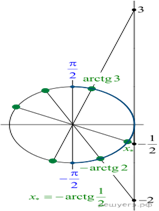 Заметим,
что по формуле приведения
Заметим,
что по формуле приведения
![]()
![]()
а потому правая часть равна нулю. Тогда уравнение принимает вид
![]()
![]()
а значит, является однородным тригонометрическим уравнением
третьей степени. Разделив обе части уравнения на ![]() получим кубическое уравнение относительно
тангенса:
получим кубическое уравнение относительно
тангенса:
![]()
Обозначим ![]() и решим его
методом группировки:
и решим его
методом группировки:
![]()
![]()
![]()
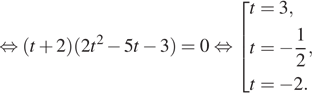
Итак, ![]()
![]()
![]() откуда
откуда ![]()
![]()
![]() соответственно.
соответственно.
Отбор корней проведем на тригонометрической окружности
(см. рис.). На отрезке ![]() лежат
числа
лежат
числа ![]()
![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
Пример 21.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. 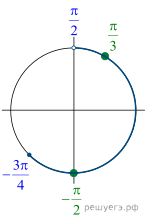 а) Преобразуем
уравнение при условии
а) Преобразуем
уравнение при условии ![]()
![]()
![]()
![]()
![]()
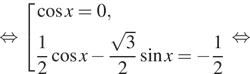
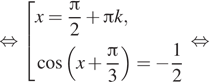
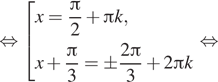
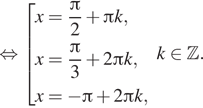
Последняя серия не подходит, поскольку ![]() Таким образом,
Таким образом, ![]()
б) Отбор корней проведем на тригонометрической
окружности (см. рис.). На заданном полуинтервале лежат два корня: ![]() и
и ![]()
Ответ:а) ![]() б)
б)
![]()
![]()
Пример 22.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение.  а) Преобразуем
уравнение:
а) Преобразуем
уравнение:
![]()
![]()
![]()
![]()
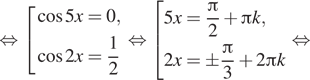
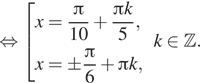
б) Отберём корни при помощи тригонометрической
окружности (см. рис.). На заданном промежутке лежат корни: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 23.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. а) Преобразуем уравнение:
![]()
Заметим, что ![]() и
и ![]() Поэтому последнее равенство может
достигаться только в случае, если
Поэтому последнее равенство может
достигаться только в случае, если ![]() а
а ![]() Решим систему уравнений:
Решим систему уравнений:
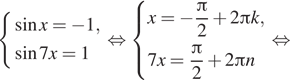
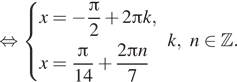
Приравняем найденные значения х, решая уравнение ![]() получим
получим
![]() Следовательно,
Следовательно,
![]()
б) Отберем корни, решая двойное неравенство:
![]()
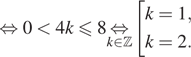 Подставим
найденные значения, получим, что на заданном промежутке лежат корни
Подставим
найденные значения, получим, что на заданном промежутке лежат корни ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
Пример 24.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение:
![]()
При ![]() получим
получим
![]() Условию
Условию ![]() соответствует только
соответствует только ![]()
При ![]() получим
получим
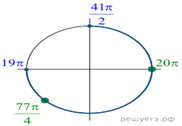
![]()
![]()
![]()
Условию ![]() соответствует
только
соответствует
только ![]()
б) Для отбора корней используем единичную
окружность. На заданном промежутке лежат корни ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
Пример 25.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 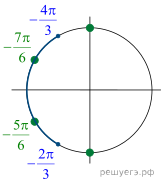 а) Преобразуем
уравнение:
а) Преобразуем
уравнение:
![]()
![]()
![]()
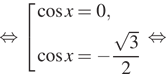
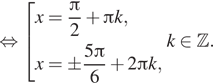
б) Корни, принадлежащие заданному отрезку,
отберём корни при помощи тригонометрической окружности (см. рис.).
Получим: ![]()
![]()
Ответ: а) ![]() ;
б)
;
б) ![]()
![]()
Пример 26.
а) Решите уравнение ![]()
б) Укажите корни этог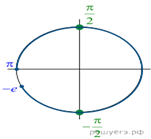 о
уравнения, принадлежащие отрезку
о
уравнения, принадлежащие отрезку ![]()
Решение. а) Используем формулу разности квадратов, затем формулы суммы и разности синусов:
![]()
![]()
![]()
![]()
![]()
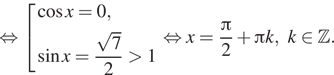
б) Отберём корни при помощи единичной
окружности. Получим ![]()
Ответ: а) ![]() б)
б)
![]()
Пример 27.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение.  а) Заметим,
что
а) Заметим,
что
![]()
![]()
![]()
![]()
![]()
Далее получаем:
![]()
![]()
![]()
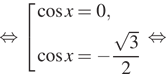
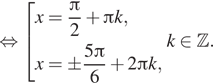 б) Отберём
корни при помощи единичной окружности (см. рис.). Подходят числа
б) Отберём
корни при помощи единичной окружности (см. рис.). Подходят числа ![]()
![]()
Пример 28. а) Решите
уравнение 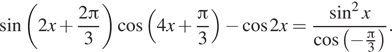
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
Решение. а) Знаменатель правой части равен ![]() Представим
уравнение как произведение синуса и косинуса, равное 1:
Представим
уравнение как произведение синуса и косинуса, равное 1:
![]()
![]()
Модули множителей не превосходят 1, поэтому возможны только два случая: оба множителя равны 1 или −1:
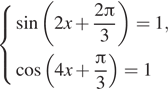 или
или
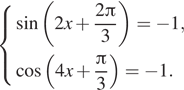
Первый случай:
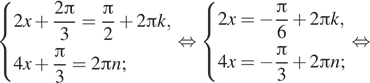
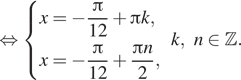
Решая полученную систему, находим: ![]() где
где
![]()
Второй случай:
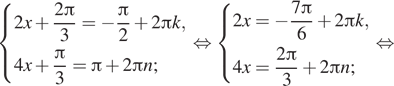
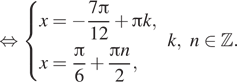
Эта система решений не имеет. Тем самым искомое решение ![]() где
где
![]()
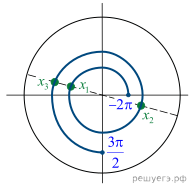
б) С помощью числовой окружности
(см. рис.) найдем корни, принадлежащие отрезку ![]() Получаем:
Получаем:
![]()
![]()
![]()
Ответ: a) ![]() б)
б)
![]()
![]()
![]()
Пример 29.а) Решите
уравнение ![]()
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
Решение. а) Преобразуем исходное уравнение:
![]()
![]()
![]()
Получится система уравнений вида:
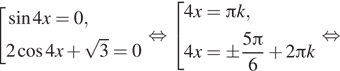
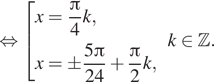
б) Проверим корни уравнения на отрезке ![]()
![]()
Получим ряд k:
![]()
При ![]()
При ![]()
При ![]()
Проверим следующий корень:
![]()
![]()
При ![]()
При ![]()
Рассмотрим последний корень:
![]()
![]()
Подставим k:
При ![]()
При ![]()
Ответ:
а) ![]() где
где ![]()
б) ![]()
Пример 30.а) Решите
уравнение ![]()
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
Решение. 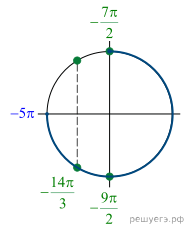 а) Преобразуем
уравнение:
а) Преобразуем
уравнение:
![]()
![]()
![]()
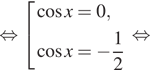
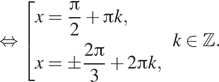
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку ![]()
Получим числа ![]()
![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
Пример 31.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 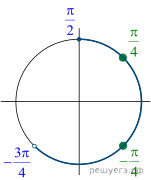 а) Для
квадратов синуса и косинуса применим в левой части формулу суммы кубов:
а) Для
квадратов синуса и косинуса применим в левой части формулу суммы кубов:
![]()
![]()
![]()
![]()
![]()
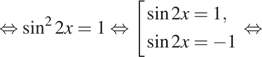
![]() б) Отберём
корни при помощи единичной окружности. Подходят
б) Отберём
корни при помощи единичной окружности. Подходят ![]() Ответ:
а)
Ответ:
а) ![]() б)
б)
![]()
Пример 32.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение:
![]()
![]()
Заметим, что
![]()
![]()
Подставив в уравнение, получим
![]()
![]()
Сделав замену ![]() получим
уравнение
получим
уравнение
![]()
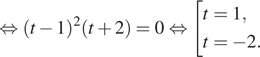
Таким образом, 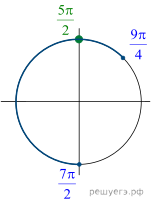
![]()
![]()

б) Отберём корни при помощи единичной
окружности. Подходит ![]()
Ответ: а) ![]() б)
б)
![]()
Приведем другое решение пункта а).
Преобразуем уравнение:
![]()
![]()
![]()
Заметим, что ![]() и
и ![]() при любом x,
следовательно, оба слагаемых не больше 0, поэтому их сумма может быть равна 0,
только если слагаемые одновременно равны 0:
при любом x,
следовательно, оба слагаемых не больше 0, поэтому их сумма может быть равна 0,
только если слагаемые одновременно равны 0:
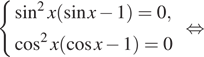
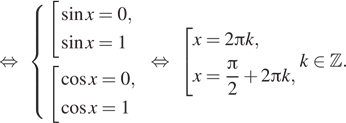
Пример 33. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 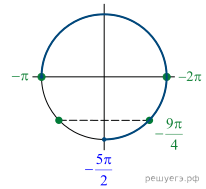 По
основному тригонометрическому тождеству
По
основному тригонометрическому тождеству ![]() Обозначим
Обозначим ![]() тогда
тогда
![]()
![]()
![]()
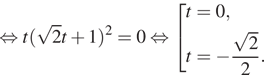
Вернемся к исходной переменной, получим:
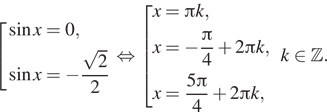
Чтобы отобрать корни, лежащие на заданном отрезке,
воспользуемся тригонометрической окружностью (см. рис.). Получим корни ![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
Примечание. Мы решили уравнение ![]() записав левую
часть в виде полного квадрата
записав левую
часть в виде полного квадрата ![]() Можно
было найти дискриминант:
Можно
было найти дискриминант: ![]() и
прийти к выводу, что уравнение имеет единственный корень
и
прийти к выводу, что уравнение имеет единственный корень
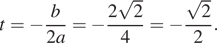
Пример 33.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 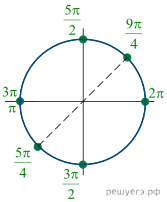 а) Преобразуем
уравнение:
а) Преобразуем
уравнение:
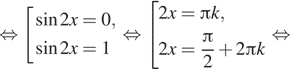
![]()
![]()
![]()
![]()
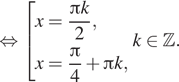 б) Отберём
корни при помощи единичной окружности. Подходят:
б) Отберём
корни при помощи единичной окружности. Подходят: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 34.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 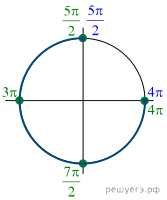 а) Преобразуем
уравнение, используя формулу разности квадратов, суммы и разности синусов:
а) Преобразуем
уравнение, используя формулу разности квадратов, суммы и разности синусов:
![]()
![]()
![]()
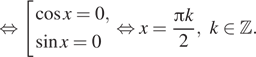
б) Отберём корни при помощи тригонометрической
окружности. Подходят ![]()
![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
![]()
Пример 35 а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение.  a) Используем
формулы понижения порядка:
a) Используем
формулы понижения порядка:
![]()
![]()
![]()
![]()
![]()
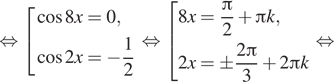
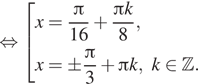
б) Отберём корни при помощи единичной
окружности. Подходят ![]()
![]()
![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
![]()
![]()
Пример 36.
а) Решите уравнение ![]()
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
Решение. 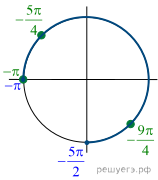 а) Запишем
исходное уравнение в виде:
а) Запишем
исходное уравнение в виде:
![]()
![]()
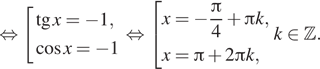
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку ![]() Получим
Получим
![]()
![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]() и
и ![]()
Пример 37.
а) Решите уравнение 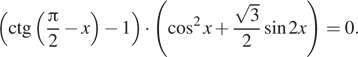
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 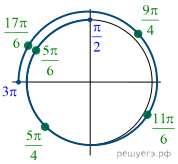 а) Преобразуем
уравнение:
а) Преобразуем
уравнение:
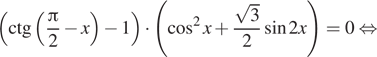
![]()
![]()

б) Отберём корни при помощи единичной
окружности. Подходят ![]()
![]()
![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
![]()
![]()
Пример 38
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 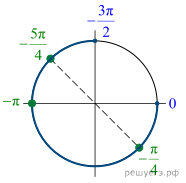 а) Логарифм
единицы равен нулю, поэтому последнее слагаемое в левой части уравнения имеет
вид
а) Логарифм
единицы равен нулю, поэтому последнее слагаемое в левой части уравнения имеет
вид ![]() Это
выражение определено при
Это
выражение определено при ![]() и для всех
таких чисел равно 1. Получаем:
и для всех
таких чисел равно 1. Получаем:
![]()
![]()
![]()


Условию ![]() соответствует
соответствует
![]() б) Отберем корни при помощи
единичной окружности (см. рис). Подходят:
б) Отберем корни при помощи
единичной окружности (см. рис). Подходят: ![]()
![]()
![]() Ответ:
а)
Ответ:
а) ![]() б)
б)
![]()
![]()
![]()
Пример 39.
а) Решите уравнение ![]()
б) Найдите все корни уравнения, принадлежащие
отрезку ![]()
Решение. а) Котангенс определен при ![]() Преобразуем уравнение при этом условии:
Преобразуем уравнение при этом условии:
![]()
![]()
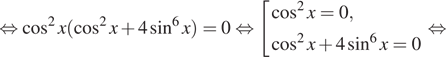
![]()
Выше мы воспользовались тем, что сумма ![]() не обращается
в нуль, поскольку косинус и синус одного угла одновременно в нуль не
обращаются.
не обращается
в нуль, поскольку косинус и синус одного угла одновременно в нуль не
обращаются.
б) Отберем корни при помощи двойного неравенства:
![]()
откуда следует, что k = 6 или k = 7.
Значения переменной, соответствующие найденным значениям k, суть ![]()
![]() Ответ:
а)
Ответ:
а) ![]() б)
б)
![]()
![]()
Решить самостоятельно.
1. а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
2. а) Решите
уравнение ![]() б) Укажите
корни, принадлежащие отрезку
б) Укажите
корни, принадлежащие отрезку ![]()
3. а) Решите
уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
4.
а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
5.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
6.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
7.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
8.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
9.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
10.а) Решите
уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
11.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
12.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
13.
. а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
14.
а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
15.
) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
16.
а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
17.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
18.
а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
19.
а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
20. а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
21. а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
Ответы на задания.
1. а) ![]() б)
б)![]() (№4)
(№4)
2.а) ![]() б)
б) ![]() (№7)
(№7)
3. а) ![]() б)
б) ![]() (№12)
(№12)
4. а) ![]() б)
б) ![]() (№15)
(№15)
5. а) ![]()
![]() б)
б) ![]()
![]()
![]() (№23)
(№23)
6. а) ![]() б)
б) ![]() (№29)
(№29)
7. а) ![]() б)
б) ![]() (№33)
(№33)
8. Ответ: а) ![]() б)
б) ![]()
![]()
![]() (№38)
(№38)
9. а)![]() б)
б)![]() (№44)
(№44)
10. а)![]() б)
б) ![]() (№45)
(№45)
11. а) ![]() б)
б) ![]()
![]() (№53)
(№53)
12. а) ![]() б)
б) ![]()
![]() (№59)
(№59)
13. а) ![]() где
где ![]() б)
б) ![]()
![]()
![]() (№62)
(№62)
14. а) ![]() где
где ![]()
б) ![]() (№63)
(№63)
15. а) ![]() б)
б) ![]()
![]()
![]() (№66)
(№66)
16. а) ![]() б)
б) ![]() (№68)
(№68)
17. а) ![]() б)
б) ![]()
![]()
![]() (№73)
(№73)
18. а) ![]() б)
б) ![]()
![]() (№82)
(№82)
19. а) ![]() б)
б) ![]()
![]() и
и ![]() (№90)
(№90)
20. а) ![]() б)
б) ![]()
![]()
![]()
![]() (№95)
(№95)
21. а) ![]() б)
б) ![]()
![]()
![]()
![]() (№101)
(№101)
Часть 2. Разложение на множители.
1. а) уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение:
![]()
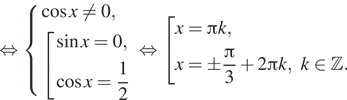
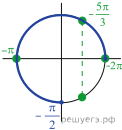
б) Отберем корни на промежутке ![]() с
помощью тригонометрической окружности. Получаем
с
помощью тригонометрической окружности. Получаем ![]() и
и
![]()
Ответ: а) ![]() б)
б) ![]()
2. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 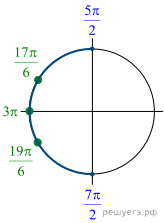 а) Запишем
уравнение в виде
а) Запишем
уравнение в виде
![]()
![]()
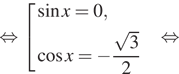
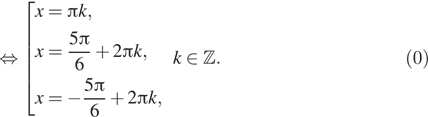
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку ![]() Получим
числа:
Получим
числа: ![]()
Ответ: а) ![]() б)
б)
![]()
3. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение.  а) Используем
формулу синуса двойного угла, выносим за скобки:
а) Используем
формулу синуса двойного угла, выносим за скобки:
![]()
![]()
![]()
![]()
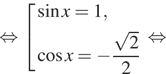
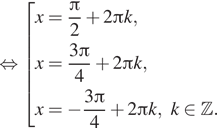
б) Изображая корни на единичной окружности, находим,
что отрезку ![]() принадлежат
корни
принадлежат
корни ![]() и
и ![]()
Ответ:а) ![]() б)
б) ![]()
4. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
промежутку ![]()
Решение.  а) Перенесём
все члены в левую часть, преобразуем и разложим левую часть на множители:
а) Перенесём
все члены в левую часть, преобразуем и разложим левую часть на множители:
![]()
![]()
![]()
1 случай. Если ![]() то
то ![]()
2 случай. Если ![]() то
то ![]() При
При ![]() решений нет. Разделим обе части уравнения на
решений нет. Разделим обе части уравнения на ![]() Получаем
Получаем ![]()
Тогда ![]()
б) Отрезку ![]() принадлежат
корни
принадлежат
корни ![]() и
и ![]()
Ответ:
а) ![]() б)
б) ![]() и
и ![]()
5. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение:
![]()
![]()
![]()
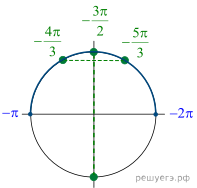
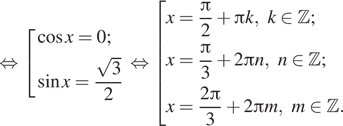
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку ![]() Получим
числа
Получим
числа ![]()
![]()
![]()
Ответ:
а) ) ![]() б)
б) ![]()
6. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) В силу нечетности и периодичности синуса имеем:
![]()
![]()
Далее им![]() еем:
еем:
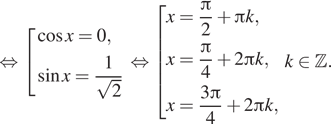
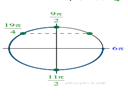
б) При помощи числовой прямой или тригонометрической
окружности (см. рис.) для каждой из задающих решения серий отберем корни
уравнения, принадлежащие отрезку ![]()
Находим три решения: ![]()
Ответ:
а) ![]() б)
б) ![]()
7. а) Решите
уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
промежутку ![]()
Решение. а) Так как
![]() и
и ![]() имеем:
имеем:
![]()
![]()
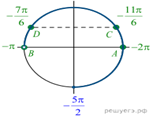
Корни уравнения: ![]()
б) Корни уравнения ![]() изображаются точками A и B, а корни
уравнения
изображаются точками A и B, а корни
уравнения ![]() —
точками C и D, промежуток
—
точками C и D, промежуток ![]() изображается
жирной дугой (см. рис.). В указанном промежутке содержатся три корня
уравнения:
изображается
жирной дугой (см. рис.). В указанном промежутке содержатся три корня
уравнения: ![]()
![]() и
и
![]()
Ответ:а) ![]() б)
б) ![]()
8. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 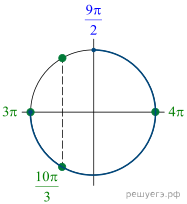 а) Преобразуем
уравнение :
а) Преобразуем
уравнение : ![]() Получаем
Получаем
![]() или
или ![]() откуда
откуда
![]() или
или
![]() где
где
![]()
б) На отрезке ![]() корни
отберем с помощью единичной окружности. Получаем
корни
отберем с помощью единичной окружности. Получаем ![]() и
и
![]()
Ответ: а) ![]() б)
б) ![]()
9. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение.  Решим уравнение:
Решим уравнение:
![]()
![]()
![]()
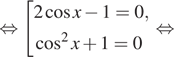
![]()
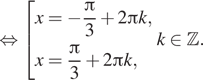
б) Укажем корни этого уравнения, принадлежащие отрезку
![]() Получим
точку
Получим
точку ![]()
Ответ: а) ![]() б)
б) ![]()
10. а) Решите
уравнение ![]()
б) Укажите корни этого
уравнения, принадлежащие отрезку ![]()
Решение. а) Имеем:
![]()
![]()
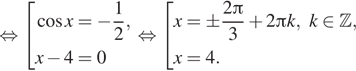
б) 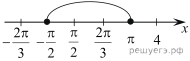 При
помощи числовой оси отберем корни, принадлежащие отрезку
При
помощи числовой оси отберем корни, принадлежащие отрезку ![]() получим
число
получим
число ![]()
Ответ:
а) ![]() б)
б) ![]()
11. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение:
![]()
![]()
![]()
![]()
![]()
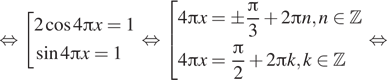
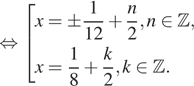
б) Ограничим каждое полученное решение из пункта «а» и решим эти неравенства:
1)
![]()
![]()
![]()
2)
![]()
![]()
![]()
![]()
3)
![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
12. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. 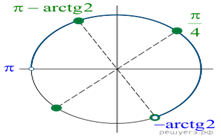 а) Решим
уравнение:
а) Решим
уравнение:
![]()
![]()
![]()
![]()
![]()
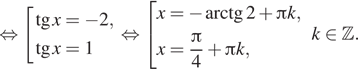
б) Отберём корни при помощи тригонометрической
окружности. Заданному условию удовлетворяют корни ![]() и
и ![]()
Ответ: а) ![]() б)
б) ![]()
13. а) Решите уравнение ![]()
б) Найдите все его корни этого уравнения,
принадлежащие отрезку ![]()
Решение. а) Запишем исходное уравнение в виде:
![]()
![]()
![]()
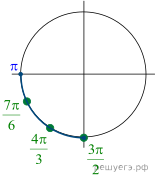
Следовательно, ![]() или
или ![]() а значит,
а значит, ![]() или
или
![]()
![]()
б) Корни, принадлежащие промежутку ![]() отберём
с помощью
отберём
с помощью
единичной окружности. Получаем: ![]()
Ответ: а) ![]() б)
б) ![]()
14. а) Решите уравнение ![]() б) Найдите все корни этого уравнения,
принадлежащие отрезку
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
Решение. 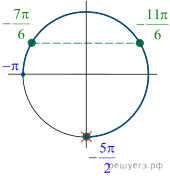 а) Запишем
исходное уравнение в виде:
а) Запишем
исходное уравнение в виде:
![]()
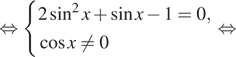
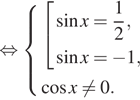
Корни уравнения ![]() не
удовлетворяют условию
не
удовлетворяют условию ![]() Тогда
получаем:
Тогда
получаем:
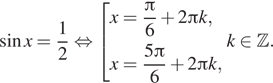
б) Отберём корни, принадлежащие промежутку ![]() с
помощью единичной окружности. Получаем
с
помощью единичной окружности. Получаем ![]()
![]()
Ответ: а) ![]() б)
б) ![]()
![]()
Решить самостоятельно.
1. а) Решите уравнение ![]() б) Укажите
корни уравнения, принадлежащие отрезку
б) Укажите
корни уравнения, принадлежащие отрезку ![]() 2. а) Решите
уравнение
2. а) Решите
уравнение ![]() б) Найдите
все корни этого уравнения, при надлежащие промежутку
б) Найдите
все корни этого уравнения, при надлежащие промежутку ![]()
3. а) Решите
уравнение ![]() б) Найдите все корни этого уравнения,
принадлежащие отрезку
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
4. а) Решите
уравнение ![]() б) Укажите корни этого уравнения, принадлежащие
отрезку
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
5. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие отрезку
![]()
6. а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие промежутку
б) Найдите
все корни этого уравнения, принадлежащие промежутку ![]()
7. а) Решите уравнение: ![]() б) Определите, какие из его корней принадлежат
отрезку
б) Определите, какие из его корней принадлежат
отрезку ![]()
8. а) Решите уравнение ![]() б) Найдите все его корни, принадлежащие отрезку
б) Найдите все его корни, принадлежащие отрезку ![]()
9. а) Решите
уравнение ![]() б) Найдите все его корни, принадлежащие отрезку
б) Найдите все его корни, принадлежащие отрезку ![]()
10. а ) Решите
уравнение ![]()
б) Найдите все корни уравнения, принадлежащие отрезку
![]()
Ответы.
1. а) ![]() б)
б) ![]()
![]()
![]() (№5)
(№5)
2. а) ![]() б)
б) ![]() (№6)
(№6)
3. а) ![]() б)
б)
![]() (№8)
(№8)
4. а) ![]() б)
б) ![]() (№10)
(№10)
5. а) ![]() б)
б) ![]()
![]()
![]() (№13)
(№13)
6. а) ![]() б)
б) ![]() (№15)
(№15)
7. а) ![]() б)
б) ![]() (№23)
(№23)
8. а) ![]() б)
б) ![]() (№28)
(№28)
9. а) ![]() б)
б) ![]() (№30)
(№30)
10. а) ![]() б)
б) ![]()
![]()
![]() 0,
0, ![]()
![]() (№34)
(№34)
Часть 3. Исследование ОДЗ.
1. ) Решите уравнение ![]()
б) Найдите все корни этого уравнения,
принадлежащие отрезку ![]()
Решение. 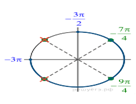 а) Заметим,
что первый множитель содержит тангенс, поэтому
а) Заметим,
что первый множитель содержит тангенс, поэтому ![]() Второй множитель —
квадратный корень, поэтому подкоренное выражение должно быть неотрицательным.
Следовательно, область определения уравнения задается неравенством
Второй множитель —
квадратный корень, поэтому подкоренное выражение должно быть неотрицательным.
Следовательно, область определения уравнения задается неравенством ![]() На
это области второй множитель не обращается в нуль. Рассмотрим случай, когда
нулю равен первый множитель. Последовательно получаем:
На
это области второй множитель не обращается в нуль. Рассмотрим случай, когда
нулю равен первый множитель. Последовательно получаем:
![]()
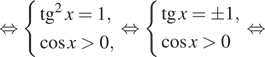
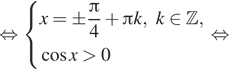
![]()
б) Корни из отрезка ![]() отберём
с помощью единичной окружности. Получаем
отберём
с помощью единичной окружности. Получаем ![]() и
и ![]() Ответ: а)
Ответ: а) ![]() б)
б)
![]()
2. а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
Решение. 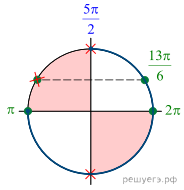 а) Получаем:
а) Получаем:
![]()
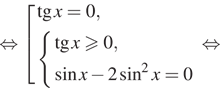
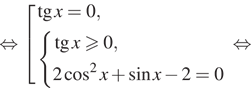
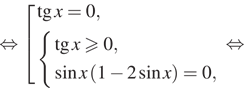
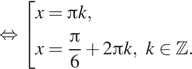
б) Корни, принадлежащие отрезку ![]() отберём
с помощью единичной окружности. Получаем
отберём
с помощью единичной окружности. Получаем ![]() и
и ![]() Ответ: а)
Ответ: а) ![]() б)
б)
![]()
![]()
3. а) Решите уравнение: ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
Решение. 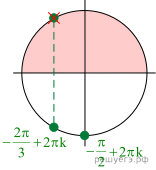
a) Решим уравнение:
![]()
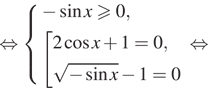
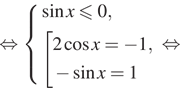
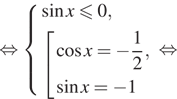
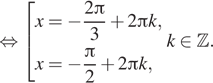
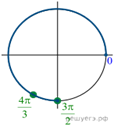
б) Корни, принадлежащие отрезку ![]() отберём
с помощью единичной окружности. Получаем
отберём
с помощью единичной окружности. Получаем ![]() и
и ![]() Ответ: а)
Ответ: а) ![]() б)
б)
![]()
4. а) Решите уравнение 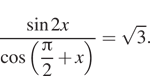 б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
Решение. а) Используя формулу синуса двойного угла и формулу приведения, имеем:
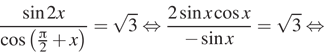
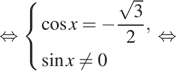
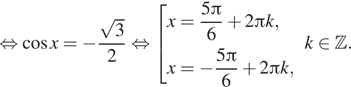
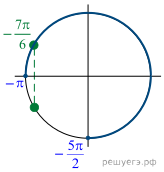
б) При помощи единичной окружности находим, что
отрезку ![]() принадлежит
только корень
принадлежит
только корень ![]()
Ответ: а) ![]() б)
б)
![]()
5. а) ешите уравнение 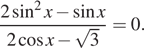 б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
Решение. а) Левая
часть уравнения определена при ![]() то
есть при
то
есть при ![]() Числитель
дроби должен быть равен нулю:
Числитель
дроби должен быть равен нулю:
![]()
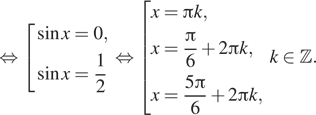
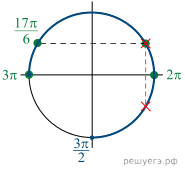
Серию ![]() нужно
отбросить. Получаем ответ:
нужно
отбросить. Получаем ответ: ![]()
б) При помощи тригонометрической окружности отберём
корни, лежащие на отрезке ![]()
![]()
![]()
Ответ: а) ![]() б)
б)
![]()
6. а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
Решение. а) Область
определения данного уравнения задается условием ![]()
При этом условии имеем: ![]()
![]() откуда
откуда
![]() или
или ![]()
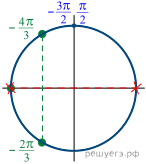 Корни уравнения
Корни уравнения ![]() не
удовлетворяют условию
не
удовлетворяют условию ![]() а из уравнения
а из уравнения ![]() получаем
получаем
![]() или
или
![]()
б) Из найденных решений промежутку ![]() принадлежат
числа
принадлежат
числа ![]()
Ответ: а) ![]() б)
б)
![]()
7. а) Решите уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие промежутку
б) Найдите
все корни этого уравнения, принадлежащие промежутку ![]()
Решение. а) Решим уравнение
![]()
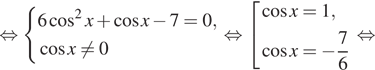
![]()
б) Найдем корни, лежащие в заданном отрезке, решая двойное неравенство:
![]()
Тогда искомый корень ![]()
Примечание.
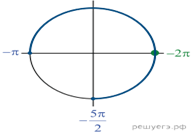
Отобрать корни можно, используя тригонометрическую окружность (см. рис.).
Ответ: а) ![]() б)
б)
![]()
8. а) Решите уравнение 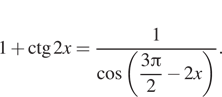 б) Укажите
корни этого уравнения, пр инадлежащие промежутку
б) Укажите
корни этого уравнения, пр инадлежащие промежутку ![]()
Решение. а) Выполним преобразования:
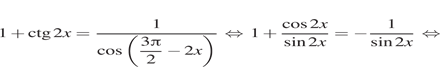
![]()

Из уравнения (1) находим:
![]()
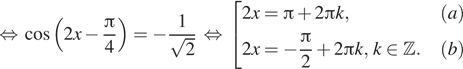
Так как решения уравнения (a) не удовлетворяют условию (2), то
окончательно получаем ![]()
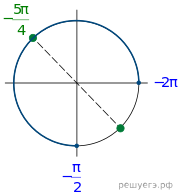
б) Из решений, найденных в пункте а), промежутку ![]() принадлежит
только одно число:
принадлежит
только одно число: ![]() Ответ: а)
Ответ: а) ![]() б)
б)
![]()
9. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 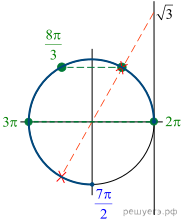 а) Перейдём
к системе:
а) Перейдём
к системе:
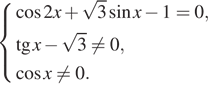
Рассмотрим первое уравнение системы:
![]()
![]()
![]()
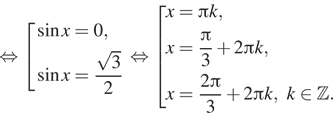
Условию ![]() удовлетворяют только
решения
удовлетворяют только
решения ![]() и
и ![]()
б) На отрезке ![]() корни
отберём с помощью единичной окружности. Получаем:
корни
отберём с помощью единичной окружности. Получаем: ![]()
Ответ: а) ![]() б)
б)
![]()
10. а) Решите
уравнение 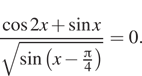
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 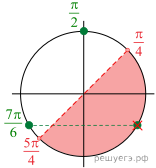 а) Найдем
область определения уравнения:
а) Найдем
область определения уравнения:
![]()
![]()
![]()
Найдем корни числителя, используем формулу ![]()
![]()
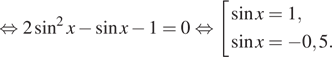
Откуда ![]()
![]()
С учетом области определения уравнения получаем:
![]()
б) Заметим, что ![]() значит,
из первой серии корней указанному отрезку принадлежит только
значит,
из первой серии корней указанному отрезку принадлежит только ![]()
Из неравенств ![]() следует,
что ни один из корней второй серии не принадлежит указанному отрезку.
следует,
что ни один из корней второй серии не принадлежит указанному отрезку.
Ответ: а) ![]() б)
б)
![]()
11. а) Решите
уравнение 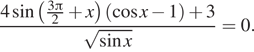
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Дробь
равна нулю, если ее числитель равен нулю, а знаменатель отличен от нуля.
Поскольку ![]() при
условии
при
условии ![]() имеем:
имеем:
![]()
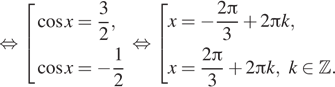
Корни первой серии не удовлетворяют условию положительности
синуса, поэтому решением уравнения являются только числа ![]()
б) Разность между соседними корнями в серии ![]() равна
2π. Поэтому на отрезке
равна
2π. Поэтому на отрезке ![]() имеющем
длину 3π, лежит ровно одно число этой серии. Это число
имеющем
длину 3π, лежит ровно одно число этой серии. Это число ![]()
Ответ: а) ![]() б)
б)
![]()
12. а) Решите
уравнение 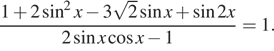
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Знаменатель
дроби не должен обращаться в нуль, то есть ![]() Преобразуем уравнение при этом условии:
Преобразуем уравнение при этом условии:
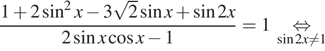
![]()
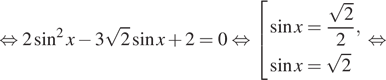
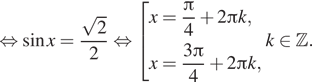
Условию ![]() удовлетворяет
только
удовлетворяет
только ![]()
![]()
б) Отберём корни при помощи двойного неравенства:
![]()
Указанному отрезку удовлетворяет только ![]()
Ответ: а) ![]() б)
б)
![]()
13. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 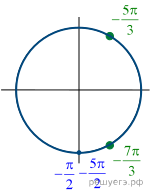 а) Заметим,
что уравнение определено при условии
а) Заметим,
что уравнение определено при условии ![]() и
и ![]() то есть
то есть ![]() Преобразуем
его при этом условии:
Преобразуем
его при этом условии:
![]()
![]()
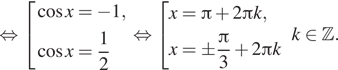
В области определения лежат только ![]()
![]()
б) Отберём корни при помощи тригонометрической
окружности. Подходят ![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
14. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 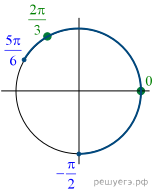 а) Преобразуем
уравнение при условиях
а) Преобразуем
уравнение при условиях ![]()
![]() :
:
![]()
![]()
![]()
![]()
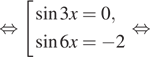
![]()
Ограничениям соответствует только ![]() откуда
откуда ![]()
б) Отберём корни при помощи тригонометрической
окружности. Подходят корни 0 и ![]()
Ответ: а) ![]() б)
0,
б)
0, ![]()
15. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение.  а) Произведение
равно нулю, когда один из множителей равен нулю, а остальные при этом
существуют. Первый множитель равен нулю, если
а) Произведение
равно нулю, когда один из множителей равен нулю, а остальные при этом
существуют. Первый множитель равен нулю, если ![]() откуда
откуда ![]() При
всех таких х второй множитель существует, поскольку он определен для
любых значений переменной.
При
всех таких х второй множитель существует, поскольку он определен для
любых значений переменной.
Рассмотрим второй случай:
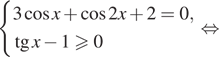
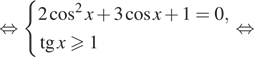
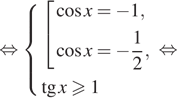
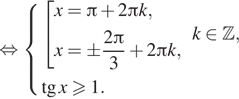
Проверим выполнение условия ![]() Числа вида
Числа вида ![]() не подходят, поскольку тангенс любого из них
равен нулю. Серия
не подходят, поскольку тангенс любого из них
равен нулю. Серия ![]() также
посторонняя, поскольку соответствующие точки лежат во второй четверти, где
тангенс отрицателен. Наконец, используя периодичность тангенса, его нечетность
и применяя формулу приведения, получаем, что для всех k:
также
посторонняя, поскольку соответствующие точки лежат во второй четверти, где
тангенс отрицателен. Наконец, используя периодичность тангенса, его нечетность
и применяя формулу приведения, получаем, что для всех k:
![]()
![]()
![]()
поэтому серия ![]() подходит.
подходит.
Объединяя случаи, заключаем, что решениями уравнения являются ![]() или
или
![]()
б) Отберём корни при помощи единичной окружности
(см. рис.), подходят числа ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
16.
а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 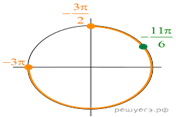 а) Перейдём
к системе:
а) Перейдём
к системе:
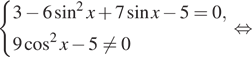
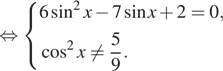
Получаем
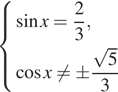
или
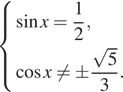
При ![]() не
выполнено условие
не
выполнено условие 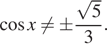 При
При
![]() находим
находим
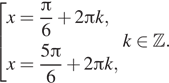
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку ![]() Получим
Получим
![]()
Ответ: а) ![]() б)
б)
![]()
17.
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 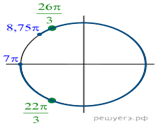 а) Упростим
правую часть уравнения:
а) Упростим
правую часть уравнения:
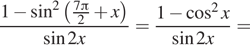
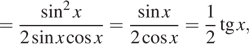
сокращать на ![]() можно при
условии
можно при
условии ![]() Далее
получаем:
Далее
получаем:
![]()
![]()
![]()
![]()
б) Отберём корни при помощи тригонометрической
окружности. Подходят ![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
18. а) Решите уравнение ![]()
б) Найдите все корни уравнения, принадлежащие отрезку
![]()
Решение. а) Уравнение определено, если
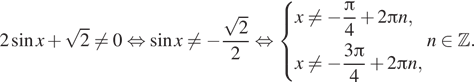
При таких значениях переменной знаменатели дробей в левой и правой
частях уравнения равны и отличны от нуля, а значит, должны быть равны числители
этих дробей. Решим уравнение: 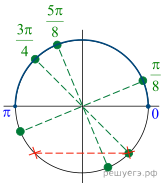
![]()
![]()
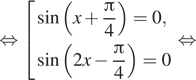
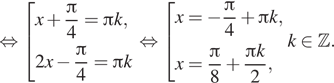
В области определения лежат серии корней ![]()
![]()
![]()
б) Отберем корни при помощи единичной окружности
(см. рис.). Подходят: ![]()
![]()
![]()
Примечание.
Выше мы решили уравнение ![]() применив формулу приведения
применив формулу приведения ![]() и
формулу разности косинусов. Можно было использовать условие равенства
косинусов:
и
формулу разности косинусов. Можно было использовать условие равенства
косинусов:
![]()
откуда в нашем случае получаем:
![]()
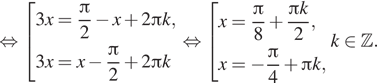
19. а) Решите уравнение ![]()
б) Найдите все корни уравнения, принадлежащие
интервалу ![]()
Решение. а) Дважды применим к левой части уравнения формулу синуса двойного угла:
![]()
![]()
откуда получаем:
![]()
Правая часть уравнения определена, если котангенс существует и
отличен от ±1, то есть при ![]()
![]() где
где
![]() Упростим
ее при этих условиях, используя формулу разности квадратов:
Упростим
ее при этих условиях, используя формулу разности квадратов:
![]()
Используем свойство пропорции и раскроем скобки:
![]()
![]()
В силу формулы ![]() получаем:
получаем:
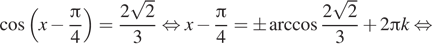

б) Интервал ![]() можно
получить поворотом интервала
можно
получить поворотом интервала ![]() на
угол –2π, поэтому достаточно найти решения, лежащие на интервале
на
угол –2π, поэтому достаточно найти решения, лежащие на интервале ![]() а
затем уменьшить их на –2π.
а
затем уменьшить их на –2π.
Заметим, что 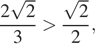 а
потому в силу убывания арккосинуса
а
потому в силу убывания арккосинуса
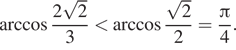
Следовательно,
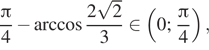
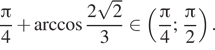
Интервалу ![]() принадлежат
корни на –2π меньшие, то есть числа:
принадлежат
корни на –2π меньшие, то есть числа:
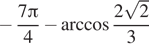
и
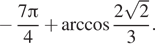
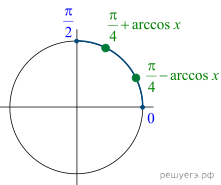
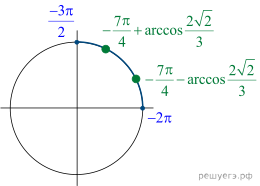
Корни на интервале ![]()
Решить самостоятельно.
1. а) Решите уравнение: ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
2. а) Решите уравнение: ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
3. а) Решите уравнение 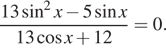 б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
4. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащего
отрезку ![]()
5. а) Решите
уравнение ![]() б) Найдите
все корни этого уравнения, принадлежащие отрезку
б) Найдите
все корни этого уравнения, принадлежащие отрезку ![]()
6. a) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие промежутку
б) Укажите
корни этого уравнения, принадлежащие промежутку ![]()
7. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
8. а) Решите уравнение ![]()
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
9. а) Решите уравнение ![]() б) Укажите
корни этого уравнения, принадлежащие отрезку
б) Укажите
корни этого уравнения, принадлежащие отрезку ![]()
10. а) Решите уравнение 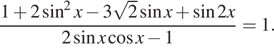
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Ответы.
1. а) ![]() б)
б)
![]() (№4)
(№4)
2. а) ![]() б)
б)
![]() (№6)
(№6)
3. а) ![]()
![]() б)
б)
![]() (№11)
(№11)
4. а) ![]() б)
б)
![]() (№13)
(№13)
5. а) ![]() б)
б)
![]() (№20)
(№20)
6. а) ![]() б)
б)
![]() (№23)
(№23)
7. а) ![]() б)
б)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (№29)
(№29)
8. а) ![]() б)
б)
![]() (№33)
(№33)
9. а) ![]() б)
б)
![]()
![]() (№35)
(№35)
10. а) ![]() б)
б)
![]()
![]() (№37)
(№37)
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.