
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ
АКАДЕМИК СӘТБАЕВ АТЫНДАҒЫ ЕКІБАСТҰЗ ИНЖЕНЕРЛІК - ТЕХНИКАЛЫҚ ИНСТИТУТЫНЫҢ КОЛЛЕДЖІ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
ЕКИБАСТУЗСКИЙ КОЛЛЕДЖ ИНЖЕНЕРНО - ТЕХНИЧЕСКОГО ИНСТИТУТА ИМЕНИ АКАДЕМИКА САТПАЕВА

|
|
БЕКIТЕМIН |
|
|
Директордың ОЖ бойынша орынбасары |
|
|
|
|
|
УТВЕРЖДАЮ |
|
|
Зам. директора по УР |
|
|
|
|
|
______________ Л.Х. Шугурова |
|
|
|
|
|
«____» ___________ 20 ___ж/г |
|
|
|
УЧЕБНОЕ ПОСОБИЕ
по дисциплине Основы технической механики
для учащихся технических специальностей
Автор ___________________Иконникова Татьяна Ивановна
2015
СОДЕРЖАНИЕ
1. Учебное пособие по дисциплине «Основы технической механики»для выполнения лабораторных, практических и самостоятельных работ
7. Лабораторная работа 1 по теме
«Определение центра тяжести плоских фигур»
8. Лабораторная работа 2 по теме
«Определение модуля продольной упругости»
9. Лабораторная работа 3 по теме
«Испытание на кручение стального образца»
ВВЕДЕНИЕ
Дисциплина «Основы технической механики» является важной общетехнической дисциплиной, назначение которой – дать будущим техникам основные сведения о законах равновесия и движения материальных тел, о методах расчета элементов машин и сооружений на прочность, жесткость и устойчивость. Знания и навыки, полученные при изучении этой дисциплины, являются основой для освоения смежных специальных дисциплин.
В учебном процессе колледжа выделяют два вида самостоятельной работы: аудиторную и внеаудиторную.
Аудиторная самостоятельная работа (в дальнейшем практические и лабораторные работы) по дисциплине выполняется на учебных занятиях под непосредственным руководством преподавателя и по его заданию.
Внеаудиторная самостоятельная работа (в дальнейшем самостоятельная работа) выполняется студентом по заданию преподавателя, но без его непосредственного участия.
При проведении лабораторных и практических работ используется как фронтальная, так и групповая формы организации занятий, а при выполнении самостоятельных работ используется индивидуальная форма организации работы студентов.
Лабораторные, практические и самостоятельные работы студентов проводится с целью:
- систематизации и закрепления полученных теоретических знаний и практических умений студентов;
- углубления и расширения теоретических знаний;
- формирования умений использовать нормативную, справочную документацию и специальную литературу;
- развития познавательных способностей и активности студентов: творческой инициативы, самостоятельности, ответственности и организованности;
- формирования самостоятельности мышления, способностей к саморазвитию, самосовершенствованию и самореализации;
- развития исследовательских умений.
Лабораторные, практические и самостоятельные занятия могут носить репродуктивный, частично - поисковый характер.
В современной образовательной сфере важное место занимают электронные средства обучения. В связи с этим разработанное электронное методическое пособие по дисциплине «Техническая механика» является актуальным, имеет практическую ценность и направлена на повышение качества образования.
Данное пособие предназначено для реализации Государственных требований к минимуму содержания и уровню подготовки выпускников по специальностям:
0707000 - Техническое обслуживание и ремонт горного электромеханического оборудования
0711000 - Маркшейдерское дело
0901000 - Электрооборудование электростанций, и сетей (по видам)
0907000 - Теплотехническое оборудование и системы теплоснабжения (по видам)
1108000 - Эксплуатация, ремонт и техническое обслуживание подвижного состава железных дорог (по видам)
При создании пособия были поставлены следующие задачи:
- обеспечение качественной реализации Государственного образовательного стандарта профессионального образования;
- освоение практических приемов решение задач и выполнения лабораторных работ;
- активизация позновательной деятельности студентов;
- приобретение навыков самообучения;
- контроль процесса усвоения знаний.
Исходя из поставленных учебных целей, в данное пособие включены:
- учебные элементы с практическими упражнениями;
- учебные элементы самооценки прогресса в обучении;
- элементы сопровождения учебной дисциплины (учебные цели; оглавление практических, лабораторных и самостоятельных работ; последовательность действий для выполнения практических и расчетно-графических работ; индивидуальные задания для выполнения лабораторных и самостоятельных работ ; задания для бригад; контрольные вопросы для самопроверки; список литературы).
1.1 Дисциплина «Основы технической механики» состоит из трех разделов:
- теоретическая механика;
- сопротивление материалов
- основы конструировния и детали машин
По этим разделам рекомендуются следующие виды заданий для самостоятельной работы:
- для овладения знаниями: чтение текста (учебника, дополнительной литературы), конспектирование текста, работа со справочниками, использование компьютерной техники и Интернета и др;
- для закрепления и систематизации знаний: составление тематических кроссвордов, ответы на контрольные вопросы, тестирование и др;
- для формирования умений: решение вариативных задач, подтверждение закономерностей, ознакомление с методиками проведения экспериментов, выполнение расчетно-графических работ и др.
Продуманное и целесообразное использование видов заданий для организации самостоятельной работы студентов не создает перегрузку, а наоборот, вызывает у студентов повышенный интерес к изучаемой дисциплине, помогает усвоению и закреплению учебного материала. Виды заданий для аудиторной и внеаудиторной самостоятельных работ, их содержание могут иметь дифференцированный характер, учитывая индивидуальные особенности студентов.
1.2 При работе с учебником рекомендуется следующая последовательность изучения материала:
- ознакомиться с заданием самостоятельной работы;
- изучить теоретический материал вопроса. Если вопрос имеет большой объем, надо разбить его на отдельные части;
- записать аккуратно в конспект основные определения, доказательства, правила и формулы, сопровождая выписки схемами и рисунками. Конспект поможет в подготовке к теоретической части экзамена;
- в целях закрепления теоретического материала и приобретения навыков в пользовании расчетными формулами, уравнениями законов и теорем, необходимо разобрать примеры и задачи, помещенные в учебнике, и решить задачи из сборников задач по соответствующему разделу.
При изучении теоретического материала студенты могут использовать Интернет.
1.3 При составлении кроссворда необходимо использовать термины и понятия соответствующей темы. Кроссворд составляется в произвольной форме, оформляется на отдельном листе формата А 4 и должен содержать не менее 10 слов.
1.4 Используя компьютерную технику, студенты могут оформить тематические кроссворды, расчетно-графические работы.
Расчетно-графическая работа состоит из графической и текстовой частей. Текстовую часть работы следует выполнять на листах формата А4 в соответствии с требованиями к текстовым документам по ГОСТ 2.105-95.
Графическую часть можно оформить на листах текстовой части или отдельно на миллиметровой бумаге.
1.5 При оформлении самостоятельных работ соблюдать следующие требования:
- работы надо выполнять аккуратным почерком с интервалами между строками;
- тексты условий задач переписывать обязательно, рисунки к задачам должны быть выполнены четко;
- решение задачи делить на пункты. Каждый пункт должен иметь подзаголовок с указанием, что и как определяется, по каким формулам или на основе каких теорем, законов, правил, методов;
- преобразования формул, уравнений в ходе решения производить в общем виде, а уже затем подставлять исходные данные. Порядок подстановки числовых значений должен соответствовать порядку расположения в формуле буквенных обозначений этих величин. После подстановки исходных значений вычислить окончательный результат;
- при решении задач применять только Международную систему единиц (СИ), а также кратные и дольные от них.
- тщательно проверить правильность всех вычислений, обратив особое внимание на соблюдение правильности размерностей, подставляемых в формулу значений, оценить правдоподобность полученного ответа.
1.6 Изучив и законспектировав теоретический материал той или иной темы, решив задачу расчетно-графической работы и т.д., студент должен проверить себя. Опыт прочного усвоения материала темы показывает, что самопроверку проводить необходимо. Для этого в каждом задании помещены контрольные вопросы. Прочитав вопрос надо дать на него полный исчерпывающий ответ, не пользуясь при этом ни конспектом, ни учебником.
САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Тема: Основные понятия и аксиомы статики
Изучение вопроса «Свободные и несвободные тела, связи».
После выполнения самостоятельной работы студент должен:
- иметь представление о свободном и несвободном телах, о видах связей и их реакциях;
- знать о принципе освобождения от связей, направлениях реакций основных типов связей.
Задание для самостоятельной работы 1
Изучить теоретический материал и составить конспект, раскрывая следующие понятия:
а) свободное и несвободное тела;
б) связи, виды связей;
в) реакции и направления реакций идеальных связей;
г) принцип освобождения от связей.
Контрольные вопросы
а) могут ли уравновешиваться силы действия противодействия двух тел?
б) к какому телу приложена реакция опоры: к самой опоре или к опирающемуся телу?
в)укажите связи (опоры), для которых реакции всегда направлены по нормали к поверхности;
г) вставьте пропущенные слова:
Не изменяя равновесия тела, связи можно отбросить, а их действия реакциями.
д) перечислите наиболее распространенные виды связей, встречающиеся в механике.
Литература: [2] c.12-16; [3] c.10-12; [9] c.7-11.
ПРАКТИЧЕСКАЯ РАБОТА 1
Тема: Плоская система сходящихся сил
После выполнения практической работы студент должен:
- знать геометрический и аналитический способы определения равнодействующей силы, условия равновесия системы сил;
- уметь определить равнодействующую системы сходящихся сил геометрическим и аналитическим способами; применять уравнения равновесия при решении практических задач.
Тестовый контроль
Варианты тестового контроля приведены в таблицах 3…10.
Расчетные формулы:
а) равнодействующая плоской системы сходящихся сил R, Н
![]() =
= ![]() ,
,
где ![]() - проекции равнодействующей на
оси координат, Н;
- проекции равнодействующей на
оси координат, Н;
![]() ,
,![]() -
алгебраическая сумма проекции векторов сил системы на оси координат, Н.
-
алгебраическая сумма проекции векторов сил системы на оси координат, Н.
б) угол
равнодействующей с осью Ох ![]() , град
, град
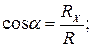
![]() .
.
в) аналитическое условие условия равновесия плоской системы сходящихся сил
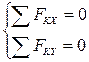
При геометрическом способе определения равнодействующей системы сходящихся сил необходимо построить силовой многоугольник. Если при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодействующая R системы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил будет находиться в геометрическом условии равновесия.
Вариант 1
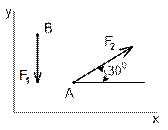
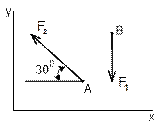
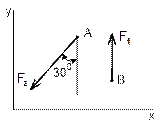
Рисунок 1 Рисунок 2 Рисунок 3
Таблица 3
|
Вопросы |
Ответы |
||
|
1 |
2 |
3 |
|
|
1 На каком рисунке сила F1 имеет положительную проек- цию на ось Y? |
1 |
2 |
3 |
|
2 Чему равна проекция силы F1 на ось Y на рисунке 3? |
– F1 |
F1·cos 0° |
– F1·cos 0° |
|
3 Чему равна проекция сил на ось Y на рисунке 2? |
– F1+ |
– F1+F2sin30° |
–F2·cos30°+F1 |
|
4 Чему равна проекция сил на ось X на рисунке 3? |
F2·cos 30°+ |
– F2·cos 30° |
– F2·cos
60°+ |
|
5 Чему равна проекция силы F2 на ось X на рисунке 2? |
F2·cos 30° |
– F2·cos 30° |
– F2·sin 30° |
|
6 Чему равна проекция силы F2 на ось Y на рисунке 3? |
F2·sin 30° |
F2·cos 60° |
– F2·cos 30° |
|
7 На каком рисунке сила F2 имеет две положительные проекции? |
1 |
2 |
3 |
|
8 На каком рисунке сила F2 имеет две отрицательные проекции? |
1 |
2 |
3 |
|
9 На каком рисунке сила F2 имеет положительную проек-цию на ось Y, а отрицательную на ось Х? |
1 |
2 |
3 |
|
10 На каком рисунке сила F2 имеет положительную проек-цию на ось Х? |
1 |
2 |
3 |
Вариант 2
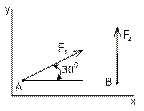
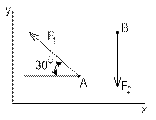
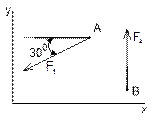
Рисунок 4 Рисунок 5 Рисунок 6
Таблица 4
|
Вопросы |
Ответы |
||
|
1 |
2 |
3 |
|
|
1 На каком рисунке сила F1 имеет положительную проекцию на ось Х?
|
4 |
5 |
6 |
|
2 На каком рисунке сила F2 имеет отрицательную проекцию на ось Y?
|
4 |
5 |
6 |
|
3 Чему равна проекция силы F2 на ось Y на рисунке 5?
|
F2·cos 0° |
– F2 |
F2 |
|
4 На каком рисунке сила F1 имеет две отрицательные проекции?
|
4 |
5 |
6 |
|
5 На каком рисунке сила F1 имеет две положительные проекции? |
4 |
5 |
6 |
|
6 Чему равна проекция силы F1 на ось Y на рисунке 5?
|
F1·cos 30° |
F1·sin 30° |
– F1·cos 60° |
|
7 Чему равна проекция силы F1 на ось X на рисунке 6?
|
F1·cos 30° |
– F1·cos 30° |
– F1·sin 30° |
|
8 Укажите сумму проекции сил на ось Y на рисунке 6
|
F1·cos 60°+ F2 |
– F2+F1cos30° |
F2 – F1·sin 30° |
|
9 Укажите сумму проекции сил на ось Х на рисунке 4
|
–
F1·cos 30° |
– F1·sin 60° |
F1·cos 30° |
|
10 Укажите сумму проекции сил на ось Y на рисунке 5 |
F1·sin 30°+ F2 |
F2 – F1·cos60° |
- F2+F1·sin30° |
Вариант 3
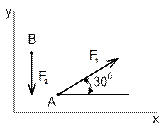
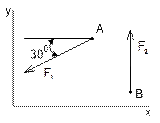
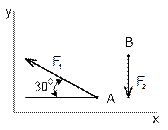
Рисунок 7 Рисунок 8 Рисунок 9
Таблица 5
|
Вопросы |
Ответы |
||
|
1 |
2 |
3 |
|
|
1 На каком рисунке сила F2 имеет положительную проекцию на ось Y? |
7 |
8 |
9 |
|
2 Чему равна проекция силы F2 на ось Y на рисунке 8? |
– F2 |
– F2·cos0° |
F2 |
|
3 Чему равна проекция сил на ось Y на рисунке 8? |
F2 - F1cos60° |
–F2 + F1·sin 30° |
F1·cos60° –F2 |
|
4 Чему равна проекция сил на ось Х на рисунке 9? |
– F1·cos 30° |
– F2 –F1·cos30°
|
F1·cos30° |
|
5 Чему равна проекция силы F1 на ось Y на рисунке 9? |
F1·cos 60° |
– F1·sin 30° |
– F1·cos60° |
|
6 Чему равна проекция силы F1 на ось Х на рисунке 9? |
F1·cos 30° |
– F1·cos 30° |
F1·sin 60° |
|
7 На каком рисунке сила F1 имеет две отрицательные проекции? |
7 |
8 |
9 |
|
8 На каком рисунке сила F1 имеет две положительные проекции? |
7 |
8 |
9 |
|
9 На каком рисунке сила F2 имеет положительную проекцию на ось Y? |
7 |
8 |
9 |
|
10 На каком рисунке сила F1 имеет положительную проекцию на ось Х? |
7 |
8 |
9 |
Вариант 4

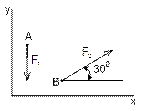
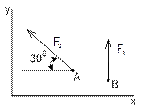
Рисунок 10 Рисунок 11 Рисунок 12
Таблица 6
|
Вопросы |
Ответы |
||
|
1 |
2 |
3 |
|
|
1 На каком рисунке сила F2 имеет две положительные проекции? |
10 |
11 |
12 |
|
2 На каком рисунке сила F2 имеет две отрицательные проекции? |
10 |
11 |
12 |
|
3 На каком рисунке сила F2 проектируется положительно на ось Х?
|
10 |
11 |
12 |
|
4 На каком рисунке сила F1 имеет отрицательную проекцию на ось Y? |
10 |
11 |
12 |
|
5 Чему равна проекция силы F2 на ось Х на рисунке 11?
|
– F2·sin 60° |
F2·cos 30° |
– F2·cos 30° |
|
6 Чему равна проекция силы F2 на ось Y на рисунке 10?
|
F2· sin 30° |
– F2· cos 60° |
F2· cos 60° |
|
7 Чему равна проекция сил на ось Y на рисунке 12?
|
F2· cos 60°+F |
F2·cos60°+ F1 |
– F1 + F2·sin 30° |
|
8 На каком рисунке сила F2 имеет положительную проекцию на ось Y, отрицатель - ную проекцию на ось Х? |
10 |
11 |
12 |
|
9 На каком рисунке сумма всех сил на ось Y положительная?
|
10 |
11 |
12 |
|
10 Чему равна проекция силы F2 на ось Х на рисунке 12 ? |
F2· cos30° |
– F2· cos 30° |
F2· sin 60° |
Вариант 5
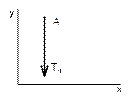

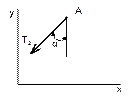
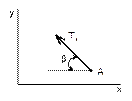
Рисунок 13 Рисунок 14 Рисунок 15 Рисунок 16
Таблица 7
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Какая сила имеет две отрицательные проекции?
|
Т1 |
Т2 |
Т3 |
Т4 |
|
2 Какая сила имеет положитель- ную проекцию на ось Y и отрицательную - на ось Х?
|
Т1 |
Т2 |
Т3 |
Т4 |
|
3 Какая сила имеет проекцию на ось Х, равную нулю?
|
Т1 |
Т2 |
Т3 |
Т4 |
|
4 Какая сила имеет проекцию на ось Y, равную нулю?
|
Т2 |
Т3 |
Т4 |
Т1 |
|
5 Чему равна проекция силы Т2 на ось Х?
|
0 |
Т2 |
– Т2 |
– Т2· cos 0° |
|
6 Чему равна проекция силы Т1 на ось Y?
|
0 |
Т1 |
– Т1 |
– Т1· cos90° |
|
7 Чему равна проекция силы Т3 на ось Х?
|
Т3· sin α |
– Т3· sin α |
Т3· cos α |
– Т3· cos a |
|
8 Чему равна проекция силы Т3 на ось Y?
|
– Т3· sin α |
Т3· sin α |
– Т3· cos α |
Т3· cos α |
|
9 Чему равна проекция силы Т4 на ось Х?
|
Т4· sin β |
– Т4· sin b |
Т4· cos β |
– Т4· cos β |
|
10 Чему равна проекция силы Т4 на ось Y?
|
– Т4·sin β |
Т4·sin β |
Т4·cos β |
– Т4·cos β |
Вариант 6
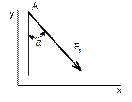
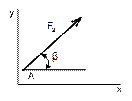
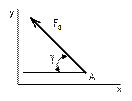
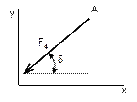
Рисунок 17 Рисунок 18 Рисунок 19 Рисунок 20
Таблица 8
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Какая сила имеет две положительные проекции?
|
F1 |
F2 |
F3 |
F4 |
|
2 Какая сила имеет две отрицательные проекции?
|
F1 |
F2 |
F3 |
F4 |
|
3 Какая сила имеет положительную проекцию на ось Х и отрицательную — на ось У? |
F1 |
F2 |
F3 |
F4 |
|
4 Какая сила имеет положительную проекцию на ось У и отрицательную — на ось Х? |
F1 |
F2 |
F3 |
F4 |
|
5 Чему равна проекция силы F1 на ось Х?
|
– F1· cos α |
F1· cos α |
– F1· sin α |
F1· sin α |
|
6 Чему равна проекция силы F2 на ось Y?
|
– F2· sin β |
F2· sin β |
F2· cos β |
– F2· cos β |
|
7 Чему равна проекция силы F4 на ось Х?
|
– F4· cos δ |
F4· sin δ |
– F4· sin δ |
F4· cos δ |
|
8 Чему равна проекция силы F3 на ось Х?
|
– F3· cos γ |
F3· cos γ |
F3· sin γ |
– F3· sin γ |
|
9 Чему равна проекция силы F1 на ось Y?
|
F1· cos α |
– F1· sin α |
F1· sin α |
– F1· cos α |
|
10 Чему равна проекция силы F4 на ось Y?
|
– F4· cos δ |
F4· sin δ |
F4· cos δ |
– F4· sin δ |
Вариант 7
Рисунок 21 Рисунок 22 Рисунок 23 Рисунок 24
Таблица 9
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Какая сила имеет две отрицательные проекции? |
Q1 |
Q2 |
Q3 |
Q4 |
|
2 Какая сила имеет две положительные проекции?
|
Q4 |
Q2 |
Q1 |
Q3 |
|
3 Какая сила имеет положительную проекцию на ось Y и отрицательную — на ось Х |
Q1 |
Q2 |
Q3 |
Q4 |
|
4 Какая сила имеет положительную проекцию на ось Х и отрицательную — на ось Y? |
Q1 |
Q2 |
Q3 |
Q4 |
|
5 Чему равна проекция силы Q2 на ось Х?
|
– Q2· sin β |
Q2· sin β |
– Q2·cos β |
Q2· cos β |
|
6 Чему равна проекция силы Q3 на ось Y?
|
– Q3· sin γ |
Q3· cos γ |
– Q3· cos γ |
Q3· sin γ |
|
7 Чему равна проекция силы Q4 на ось Х?
|
– Q4· cos δ |
Q4· cos δ |
Q4· sin δ |
– Q4· sin δ |
|
8 Чему равна проекция силы Q1 на ось Х?
|
– Q1· sin α |
Q1· sin α |
– Q1·cos α |
Q1· cos α |
|
9 Чему равна проекция силы Q2 на ось Y? |
Q2· sin β |
– Q2·cos β |
– Q2· sin β |
Q2· cos β |
|
10 Чему равна проекция силы Q4 на ось Y?
|
Q4· sin δ |
– Q4· cos δ |
– Q4· sin δ |
Q4· cos δ |
Вариант 8
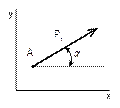
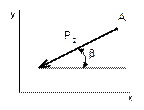
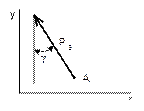
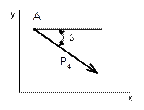
Рисунок 25 Рисунок 26 Рисунок 27 Рисунок 28
Таблица 10
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Какая сила имеет две положительные проекции?
|
P1 |
P2 |
P3 |
P4 |
|
2 Какая сила имеет две отрицательные проекции?
|
P1 |
P2 |
P3 |
P4 |
|
3 Какая сила имеет положительную проекцию на ось Х и отрицательную - на ось Y?
|
P1 |
P2 |
P3 |
P4 |
|
4 Чему равна проекция силы P1 на ось Х?
|
– P1·cos α |
P1·cos α |
P1·sin α |
– P1·sin α |
|
5 Чему равна проекция силы P2 на ось Y?
|
P2· sin β |
– P2· sin β |
P2· cos β |
– P2· cos β |
|
6 Чему равна проекция силы P3 на ось Х?
|
P3· cos γ |
P3· sin γ |
– P3· sin γ |
– P3· cos γ |
|
7 Чему равна проекция силы P4 на ось Y?
|
– P4 · cos δ |
P4· cos δ |
– P4·sin δ |
P4· sin δ |
|
8 Чему равна проекция силы P4 на ось Х?
|
– P4· sin δ |
P4· sin δ |
– P4· cos δ |
P4· cos δ |
|
9 Чему равна проекция силы P1 на ось Y
|
P1· sin α |
– P1· sin α |
P1· cos α |
– P1· cos α |
|
10 Чему равна проекция силы P3 на ось Y?
|
– P3· cos γ |
P3· cos γ |
P3· sin γ |
– P3· sin γ |
Последовательность решения задач на равновесие
плоской системы сходящихся сил
1 Выбрать тело (точку), равновесие которого следует рассматривать.
2 Освободить тело (шарнир) от связей и изобразить действующее на него активные силы и реакции отброшенных связей. Причем реакции от стержней следует направить от шарнира, так как принято предполагать, что стержни растянуты.
3 Выбрать оси координат и составить уравнения, используя условие равновесия системы сходящихся сил на плоскости åFкx = 0; åFкy = 0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно одной из неизвестных.
4 Определить реакции стержней из составленных уравнений равновесия.
5 Проверить правильность полученных результатов геометрическим способом.
6 Анализировать решение задачи.
Пример 1. Определение равнодействующей
плоской системы сходящихся сил
Определить равнодействующую плоской системы сходящихся сил двумя способами (рисунок 29),если:
F1 = 22 кН; F2 = 35 кН; F3 = 22 кН; F4 = 23 кН; F5 = 15 кН; a1 = 30 0; a2 = 60 0; a3 = 120 0; a4 = 180 0; a5 = 300 0
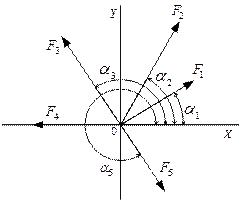
Рисунок 29
Решение
1 Равнодействующую плоской системы сходящихся сил определяем аналитическим способом.
![]() ;
;
![]()
![]() = F1х
+ F2х + F3х + F4х + F5х ,
= F1х
+ F2х + F3х + F4х + F5х ,
где F1х = ![]() F1х =
F1х = ![]() кН;
кН;
F2х = ![]() F2х =
F2х =
![]() кН;
кН;
F3х = ![]() F3х
=
F3х
= ![]() кН;
кН;
F4х = ![]() F4х =
F4х = ![]() кН;
кН;
F5х = ![]() F5х
=
F5х
= ![]() кН;
кН;
![]() 19,05 + 17,5 – 11 - 23 + 7,5
= 10,05 кН.
19,05 + 17,5 – 11 - 23 + 7,5
= 10,05 кН.
![]()
![]() = F1у + F2у + F3у + F4у + F5у,
= F1у + F2у + F3у + F4у + F5у,
где F1у = ![]() F1у
=
F1у
= ![]() кН;
кН;
F2у = ![]() F2у =
F2у =
![]() кН;
кН;
F3у = ![]() F3у = 22 ·
0,866 = 19,05 кН;
F3у = 22 ·
0,866 = 19,05 кН;
F4у = 0 F4у = 0
F5у =
![]() F5у =
F5у =
![]() кН;
кН;
![]() 11 + 30,31 + 19,05 - 12,99 =
47,37 кН;
11 + 30,31 + 19,05 - 12,99 =
47,37 кН;
![]() = 48,42 кН;
= 48,42 кН;
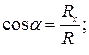
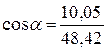 =
0,207
=
0,207 ![]()
2 Определяем равнодействующую плоской системы
сходящихся сил геометрическим (графическим) способом. С
помощью транспортира в масштабе ![]() строим
многоугольник сил (рисунок 30). Измерением определяем модуль равнодействующей
силы и угол наклона ее к оси Ох. В соответствии с рисунком 30 R гр = 47 кН;
строим
многоугольник сил (рисунок 30). Измерением определяем модуль равнодействующей
силы и угол наклона ее к оси Ох. В соответствии с рисунком 30 R гр = 47 кН; ![]()
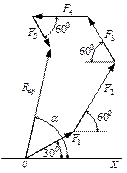
Рисунок 30
3 Анализируем решение задачи.
Результаты аналитического и геометрического
способов не должны отличаться более чем на 5 ![]() .
.
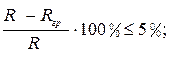
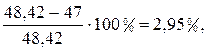 что меньше 5
что меньше 5![]() , значит условие
выполняется.
, значит условие
выполняется.
Пример 2. Определение усилий в стержнях
Определить силы, нагружающие стержни АВ и АС кронштейна в соответствии с рисунком 31, удерживающего в равновесии груз F = 6 кН и растянутую пружину, сила упругости которой F1 = 2 кН. Весом частей конструкции, а также трением на блоке пренебречь. Задачу решить аналитическим и геометрическим способами.
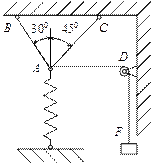
Рисунок 31
Решение
1 Определяем усилия в стержнях аналитическим способом. Рассматриваем равновесие точки схода А. К ней приложены заданные активные силы – сила натяжения троса AD, равная весу груза F и сила упругости пружины F1. Так как и трос, и пружина растянуты, то эти силы направлены от точки А.
2 Рассматривая точку А как свободную, отбрасываем связи (стержни АВ и АС), заменяя их действие реакциями RАВ и RАC. Реакции стержней направляем от точки А, предварительно полагаем стержни растянутыми (действительные направления реакций стержней в начале решения задачи неизвестны). Если наше предположение окажется неверным, то искомая реакция стержня получиться в ответе со знаком «минус»; это говорит о том, что стержень сжат и истинное направление реакции – к точке А. Полученная расчетная схема изображена на рисунке 32.

Рисунок 32
3 Принимаем обычное вертикально – горизонтальное направление координатных осей.
4 Для полученной плоской системы сходящихся сил составляем два уравнения равновесия
![]()
![]() ;
;
![]() ;
; ![]()
![]()
![]() ;
;
![]()
![]()
Решая полученную систему уравнений, находим R АВ и R AC.
R АВ = 5,86 кН и R AC = - 4,34 кН.
Замечаем, что в соответствии с предположением стержень АВ оказался растянутым, а стержень АС – сжатым.
Следует отметить, что каждое из полученных уравнений равновесия содержало два неизвестных, чего можно было бы избежать, направив координатные оси по другому, совместив одну из осей с неизвестной силой (рисунок 33). При этом в уравнении окажется лишь одно неизвестное.
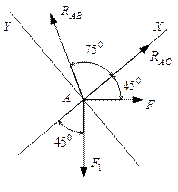
Рисунок 33
В соответствии с рисунком 33 составляем уравнения равновесия
![]()
![]() ;
;
![]()
![]() кН
кН
![]()
![]() ;
;
![]()
![]() кН.
кН.
5 Определяем усилия в стержнях геометрическим способом. В выбранном масштабе строим замкнутый силовой многоугольник. От произвольной точки О (рисунок 34) откладываем вектор заданной силы F1. От конца вектора F1 откладываем вектор заданной силы F. Затем через начало вектора F1 и конец вектора F проводим известные направления искомых реакций стержней АВ и АС. Стрелки, изображающие направление сил RАВ и RAC, ставим таким образом, чтобы в векторном многоугольнике было единое направление обхода – в данном случае против часовой стрелки.
Измеряя искомые векторы, с учетом принятого масштаба получаем:
R АВ » 5,9 кН и R AC » 4,3 кН
Точность графического решения тем выше, чем крупнее принят масштаб построения. Следует отметить, что векторный многоугольник показывает действительное, а не предполагаемое направление искомых сил.
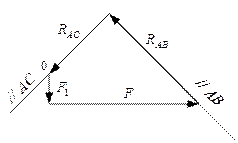
Рисунок 34
6 Анализируем решение задачи.
Результаты аналитического и
геометрического способов не должны отличаться более чем на 5 ![]() .
.
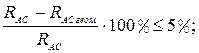
![]() < 5
< 5![]() ,
,
значит условие выполняется.
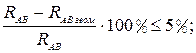
![]() < 5
< 5![]() ,
,
значит условие выполняется.
Задание для бригад
Определить равнодействующую R плоской системы сходящихся сил геометрическим и аналитическим способами. Данные взять из таблицы 11.
Таблица 11 - Исходные данные
|
Параметры |
Варианты |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
F1, кН |
12 |
8 |
20 |
3 |
6 |
|
F2, кН |
8 |
12 |
5 |
6 |
12 |
|
F3, кН |
6 |
2 |
10 |
12 |
15 |
|
F4, кН |
4 |
10 |
15 |
15 |
3 |
|
F5, кН |
10 |
6 |
10 |
9 |
18 |
|
|
30 |
0 |
0 |
15 |
0 |
|
|
45 |
45 |
60 |
45 |
15 |
|
|
0 |
75 |
75 |
60 |
45 |
|
|
60 |
30 |
150 |
120 |
150 |
|
|
300 |
270 |
210 |
270 |
300 |
6 САМОСТОЯТЕЛЬНАЯ РАБОТА
Тема: Плоская система сходящихся сил
Выполнение расчетно-графической работы 1
После выполнения самостоятельной работы студент должен:
- знать геометрический и аналитический способы определения равнодействующей силы, условие равновесия системы сходящихся сил;
- уметь определять равнодействующую системы сходящихся сил геометрическим и аналитическим способами, решать задачи на равновесие системы сходящихся сил.
6.1 Рекомендуемая последовательность для выполнения
расчетно-графической работы 1
1 Построить силовой многоугольник, откладывая силы в порядке F1, F2, F3, F4, F5. Определить величину и направление равнодействующей R геометрическим способом;
2 Построить второй силовой многоугольник, откладывая силы в порядке F5, F4, F3, F2, F1. Определить величину и направление равнодействующей R геометрическим способом;
3 Проверить правильность полученных результатов, решая задачу аналитическим способом.
6.2 Задание для самостоятельной работы
Определить значение равнодействующей силы R по величине и направлению геометрическим и аналитическим способами. Силы сходятся в начале координатных осей и составляют углы с осью Ох. Данные своего варианта взять из таблицы 12.
Таблица 12 – Данные для выполнения расчетно-графической работы 1
|
Вариант
|
Сила, Н |
Угол наклона, град |
||||||||
|
F1 |
F2 |
F3 |
F4 |
F5 |
a1 |
a2 |
a3 |
a4 |
a5 |
|
|
1 |
10 |
8 |
4 |
6 |
4 |
0 |
150 |
225 |
-45 |
135 |
|
2 |
6 |
4 |
5 |
4 |
5 |
90 |
-225 |
-45 |
0 |
60 |
|
3 |
5 |
3 |
4 |
3 |
3 |
245 |
30 |
90 |
0 |
210 |
|
4 |
6 |
4 |
4 |
5 |
4 |
60 |
90 |
-90 |
0 |
150 |
|
5 |
7 |
5 |
3 |
4 |
- |
45 |
150 |
0 |
90 |
- |
|
6 |
10 |
8 |
8 |
4 |
8 |
-60 |
50 |
120 |
180 |
45 |
|
7 |
5 |
5 |
3 |
4 |
5 |
30 |
150 |
270 |
-45 |
0 |
|
8 |
5 |
5 |
2 |
4 |
- |
0 |
45 |
-210 |
90 |
- |
|
9 |
6 |
4 |
5 |
2 |
2 |
45 |
225 |
-30 |
150 |
60 |
|
10 |
5 |
3 |
4 |
3 |
3 |
30 |
45 |
-210 |
120 |
0 |
|
11 |
10 |
5 |
15 |
20 |
25 |
-50 |
150 |
45 |
0 |
90 |
|
12 |
15 |
10 |
5 |
10 |
15 |
45 |
90 |
0 |
120 |
-210 |
|
13 |
16 |
8 |
4 |
24 |
4 |
40 |
-90 |
0 |
60 |
150 |
|
14 |
15 |
20 |
10 |
15 |
20 |
-60 |
90 |
120 |
180 |
45 |
|
15 |
5 |
4 |
5 |
3 |
2 |
45 |
210 |
0 |
180 |
60 |
|
16 |
10 |
8 |
6 |
4 |
6 |
60 |
30 |
90 |
180 |
-240 |
|
17 |
10 |
20 |
25 |
10 |
15 |
0 |
60 |
150 |
-30 |
90 |
|
18 |
6 |
3 |
9 |
12 |
15 |
60 |
240 |
0 |
150 |
-60 |
|
19 |
10 |
15 |
20 |
20 |
- |
45 |
150 |
180 |
-60 |
- |
|
20 |
15 |
30 |
45 |
60 |
15 |
60 |
-60 |
0 |
210 |
45 |
|
21 |
30 |
15 |
15 |
30 |
15 |
90 |
45 |
-150 |
-20 |
45 |
|
22 |
4 |
8 |
4 |
8 |
12 |
120 |
0 |
45 |
0 |
-45 |
|
23 |
5 |
10 |
15 |
10 |
15 |
150 |
90 |
60 |
40 |
-60 |
|
24 |
6 |
4 |
4 |
3 |
5 |
0 |
60 |
45 |
225 |
50 |
|
25 |
5 |
4 |
3 |
4 |
5 |
45 |
0 |
150 |
210 |
180 |
|
26 |
3 |
6 |
9 |
3 |
9 |
60 |
210 |
0 |
-225 |
50 |
|
27 |
10 |
15 |
20 |
30 |
15 |
30 |
150 |
-60 |
220 |
0 |
|
28 |
10 |
15 |
20 |
20 |
- |
-45 |
30 |
90 |
210 |
- |
|
29 |
5 |
5 |
2 |
4 |
3 |
-50 |
150 |
-120 |
0 |
90 |
|
30 |
4 |
5 |
8 |
8 |
4 |
60 |
0 |
225 |
45 |
240 |
6.3 Контрольные вопросы
а) по изображенным на рисунке 35 многоугольникам сил решите, сколько сил входит в каждую систему и какая из них уравновешена (обратите внимание на направление векторов)?
б) в каком случае задача на равновесие плоской системы сходящихся сил является статически определимой ?
1) когда одна сила неизвестна и по величине и по направлению;
2) когда неизвестны величины (модули) двух сил;
3)когда неизвестны величины (модули) трех сил.
в) какой вектор на рисунке 35,а является равнодействующей ?
а) б)
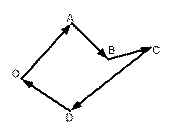
Рисунок 35
г) при каком значении угла a в соответствии с рисунком 36 (в пределах 00….1800) проекция силы F на указанную ось, будет равна:
1) нулю; 2) F; 3) – F.
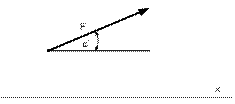
Рисунок 36
д) в соответствии с рисунком 37 можно ли определить знак проекции силы F на показанную ось?
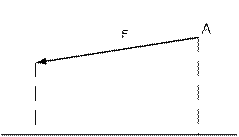
Рисунок 37
е) укажите на рисунке 37 направление оси, при котором проекция силы F будет положительной ?
ж) на рисунке 38 определите проекцию равнодействующей системы на горизонтальную ось Х, если F1 = F2 = F3 = 10 Н.
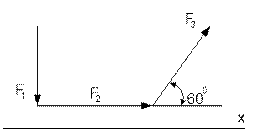
Рисунок 38
з) в каком случае плоская система сходящихся сил уравновешена?
1) Rх = 0, Rу = - 40 Н;
2) Rх = 50 Н, Rу = 0;
3) Rх = 0, Rу = 0.
и) точка А, показанная на рисунке 39,а находится в равновесии под действием четырех сил, из которых силы R1 и R2 неизвестны. При каком расположении координатных осей (случай а или б ) полученные уравнения равновесия окажутся проще ?
а) б)
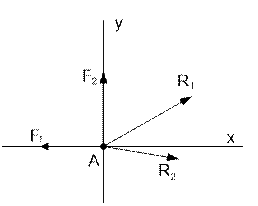
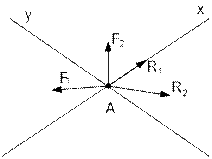
Рисунок 39
к) определите модуль и направление равнодействующей силы системы сходящихся сил, если проекции слагаемых векторов равны:
Р1Х = 50 Н; Р2Х = - 30 Н; Р3Х = 60 Н; Р4Х = 70 Н;
Р1У = - 70 Н; Р2У = 40 Н; Р3У = 80 Н; Р4У = - 90 Н;
л) из представленных на рисунке 40 силовых треугольников, выберите треугольник, построенный для точки А. Шар подвешен на нити и находится в равновесии. Обратить внимание на направление реакции от гладкой опоры и условие равновесия шара.
а) б) в) г)



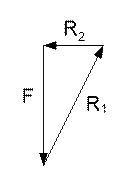
Рисунок 40
6.4 Литература: [2] c.16-27; [3] c.12-21; [9] c.12-27.
7 САМОСТОЯТЕЛЬНАЯ РАБОТА 3
Тема: Пара сил и момент силы относительно точки
Составление кроссворда.
После выполнения самостоятельной работы студент должен:
- иметь представление о силах, создающих пару; об эффекте действия пары на тело; о моменте силы относительно точки и действии его на тело;
- знать момент пары сил (обозначение, модуль, знак, единица измерения), свойства пар сил, момент силы относительно точки (обозначение, модуль, знак, единица измерения).
7.1 Задание для самостоятельной работы 3
Составить кроссворд.
7.2 Контрольные вопросы
а) чтобы определить эффект действия пары сил, надо знать:
1) величину силы и плечо пары;
2) произведение величины силы на плечо;
3) величину момента и направление.
б) пару сил можно уравновесить:
1) одной силой; 2) парой сил.
в) эффект действия пары сил на тело:
1) зависит от ее положения в плоскости;
2) не зависит от ее положения в плоскости.
г) какие из приведенных ниже пар эквивалентны?
1) сила пары 100 кН, плечо 0,5 м и сила пары 20 кН, плечо 2,5 м;
2) М1 = - 300 Н×м и М2 = 300 Н×м;
3) М1 = 10000 кгс×см и М2 = 981 Н×м.
д) момент пары сил равен 100Нм, плечо пары 0,2 м. Определите величину сил пары. Как изменится величина сил пары, если плечо увеличить в два раза при сохранении величины момента?
ж) зависят ли величина и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы?
з) почему силы пары не включаются в уравнения проекций сил системы на координатные оси?
к) определить момент результирующей пары, эквивалентной системе трех пар, лежащих в одной плоскости. Первая и третья пары вращают тело по часовой стрелке, а вторая пара вращает против часовой стрелки: F 1 = F 2 = 5кН, а 1 = 2 м; P 1 = P 2 = 10 кН, а 2 = 2 м; N 1 = N 2 = 10 кН, а 3 = 1м.
к) к телу приложены две пары, лежащие в параллельных плоскостях. Первая пара образована силами по 4 кН, имеет плечо 0,5 м и ее момент вращает по часовой стрелке. Вторая пара образована силами 6 кН, имеет плечо 0,4 м и ее момент вращает против часовой стрелки. Определить значение и направление момента пары сил, которым можно уравновесить эти пары.
7.3 Литература: [2] c.27 - 34; [3] c.21 - 27; [9] c.28 - 33.
8 ПРАКТИЧЕСКИЕ РАБОТЫ 2,3
Тема: Плоская система произвольно расположенных сил
После выполнения практических работ студент должен:
- знать три формы уравнений равновесия и применять их при определении реакций в опорах балочных систем;
- уметь определять реакции в опорах балочных систем, применяя уравнения равновесия и проверять правильность решения задач.
8.1 Тестовый контроль
Тестовый контроль по определению:
- опорных реакций двухопорной балки (таблицы: 13, 14, 15, 16);
- опорных реакций заделки (таблицы: 17, 18, 19, 20).
8.2 Последовательность решения задач на определение
опорных реакций
1 Балку освободить от связей (связи) и их (его) действие заменить силами реакций.
2 Выбрать координатные оси.
3 Составить и решить уравнения равновесия.
Реакции опор можно определить, исходя из трех форм уравнений равновесия:
а) å Fкх = 0; б) å Fкх = 0; в) åМА = 0;
å Fку = 0 åМА = 0; åМВ = 0;
åМА = 0; åМВ = 0; åМС = 0.
4 Проверить правильность решения задачи. Проверку необходимо производить по тому уравнению равновесия, которое не было использовано при решении данной задачи. (задача решена правильно лишь в том случае, если после постановки значений активных и реактивных сил в уравнение равновесия выполняется условие равновесия).
5 Сделать анализ решенной задачи (если при решении задачи реакции опор или реактивный момент получается отрицательным, то их действительное направление противоположно принятому).
Вариант 1
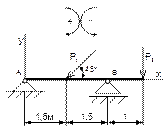



Рисунок 41 Рисунок 42 Рисунок 43 Рисунок 44
Таблица 13 - Определение опорных реакций двухопорной балки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции? |
41 |
42 |
43 |
44 |
|
2 Чему равна проекция силы Р1 на ось Х? |
-Р1∙ cos 450 |
Р1∙ sin 450 |
Р1∙ cos 450 |
Р1 |
|
3 Чему равна проекция силы Rв на ось Х? |
0 |
-Rв |
Rв |
Rв∙ cos 900 |
|
4 Чему равен момент силы Р2 относительно точки А? |
Р2 ∙ 4 |
Р2 ∙1 |
-Р2 ∙ 1 |
-Р2 ∙ 4 |
|
5 Чему равен момент силы Р1 относительно точки А |
Р1∙1,5 |
Р1 sin ∙ 45 0∙1,5 |
Р1∙3 - Р1 ∙ sin450 |
0 |
|
6 Чему равен момент силы Р1 относитель- но точки В? |
-Р1∙1,5 |
-Р1 sin 450∙1,5 |
-Р1 cos 45 0 ∙1,5 |
Р1∙1,5 |
|
7 Чему равна проекция силы RАХ на ось Y?
|
0 |
-RАХ |
RАХ |
RАХ ∙ cos 900 |
|
8 Чему равен момент силы RАХ относительно точки В?
|
RАХ ∙ 3 |
-RАХ ∙ 1,5 |
0 |
RАХ ∙ 1,5 |
|
9 Сколько уравнений равновесия надо составить для решения задачи? |
Два |
три |
одно |
Четыре |
|
10 Укажите сумму проекций сил на ось Х?
|
-RАХ – R2 |
RАХ – Р1 ∙ cos45 0 |
RАХ + Р1 ∙ sin 45 0 |
RАХ + Р1 ∙ cos45 0 |
Вариант 2
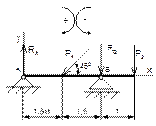
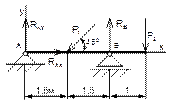
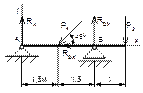

Рисунок 45 Рисунок 46 Рисунок 47 Рисунок 48
Таблица 14 - Определение опорных реакций двухопорной балки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции? |
45 |
46 |
47 |
48 |
|
2 Чему равна проекция силы Р1 на ось Х?
|
-Р1∙cos 450 |
Р1∙sin 450 |
Р1∙cos 450 |
Р1 |
|
3 Чему равна проекция силы Rв на ось Х?
|
0 |
-Rв |
Rв |
Rв∙cos 00 |
|
4 Чему равен момент силы Р2 относительно точки А?
|
Р2 ∙ 1.5 |
Р2 ∙ 4 |
0 |
-Р2 ∙ 3 |
|
5 Чему равен момент силы Р1 относительно точки А?
|
Р1∙1,5 |
Р1 ∙ sin 45 0 ∙ 1,5 |
Р1∙3 |
0 |
|
6 Чему равен момент силы Р1 относительно точки В?
|
Р1 ∙ 3 |
0 |
-Р1 ∙ sin45 0∙1,5 |
Р1∙1,5 |
|
7 Чему равна проекция силы RАХ на ось Х?
|
0 |
- RАХ |
RАХ |
RАХ ∙ cos 900 |
|
8 Чему равен момент силы RАХ относительно точки В?
|
RАХ ∙ 3 |
RАХ ∙ 1 |
0 |
RАХ ∙ 1,5 |
|
9 Сколько уравнений равновесия надо составить для решения задачи?
|
одно |
два |
три |
Четыре |
|
10 Укажите сумму проекций сил на ось Х?
|
- RАХ - R2 |
RАХ - Р1 ∙ cos450 |
RАY + RВ +Р2 |
RАY + RВ |
Вариант 3
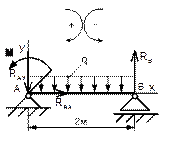
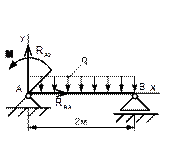
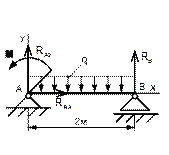
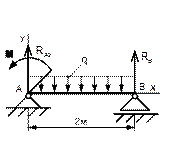
Рисунок 49 Рисунок 50 Рисунок 51 Рисунок 52
Таблица 15- Определение опорных реакций двухопорной балки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции? |
49 |
50 |
51 |
52 |
|
2 Сколько реакций дает шарнирно-подвижная опора? |
одну |
две |
три |
четыре |
|
3 Сколько реакций дает шарнирно-неподвижная опора? |
одну |
две |
три |
четыре |
|
4 Чему равна проекция момента М на ось Х?
|
М |
-М |
0 |
- |
|
5 Чему равна проекция равномерно распределенной нагрузки на ось Х? |
0 |
-q ∙ 2 |
q ∙ 2 |
- |
|
6 Какие уравнения равновесия надо составить для решения задач?
|
∑ МА = 0 ∑ МВ = 0 |
∑ FКХ = 0 ∑ FКY = 0 ∑ FКZ = 0 |
∑ FКХ = 0 ∑ МА = 0 |
∑ FКХ = 0 ∑ FКY = 0 |
|
7 Укажите сумму моментов сил относительно точки А?
|
М + q ∙ 2 - - RВ ∙ 2 |
-М + q ∙ 2 - - RВ ∙ 2 |
М - q ∙ 2 + + RАY ∙ 2 |
-М + q ∙ 2 + + RАY ∙ 2 |
|
8 Укажите сумму проекции сил на ось Х?
|
RАХ |
-RАХ |
0 |
RАХ + RАY |
|
9 Укажите сумму проекции сил на ось Y?
|
RАY – q ∙ 2 + + RВ |
RАY + q ∙ 2+ + RВ |
RАY – q ∙ 2 |
RАY + RВ |
|
10 Укажите сумму моментов сил относительно точки В?
|
М - q ∙ 2 + + RАY ∙ 2 |
М + q ∙ 2 - + RВ ∙ 2 |
-М + q ∙ 2 - - RВ ∙ 2 |
-М – q ∙ 2 + + RАY ∙ 2 |
Вариант 4
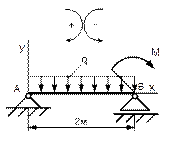
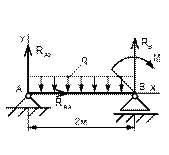
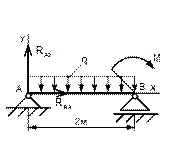
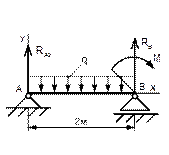
Рисунок 53 Рисунок 54 Рисунок 55 Рисунок 56
Таблица 16 - Определение опорных реакций двухопорной балки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции? |
53 |
54 |
55 |
56 |
|
2 Сколько реакций дает шарнирно-подвижная опора?
|
одну |
две |
три |
четыре |
|
3 Сколько реакций дает шарнирно-неподвижная опора? |
одну |
две |
три |
четыре |
|
4 Чему равна проекция момента М на ось Х? |
М |
-М |
0 |
4 |
|
5 Чему равна проекция равномерно распределенной нагрузки на ось Х? |
0 |
-q∙2 |
q∙2 |
10 |
|
6 Какие уравнения равновесия надо составить для решения задач? |
∑ МА = 0 ∑ МВ = 0 |
∑ FКХ = 0 ∑ FКY = 0 ∑ МА = 0 |
∑ FКХ = 0 ∑ FКY = 0 ∑ FКZ = 0 |
∑ FКХ = 0 ∑ FКY = 0 |
|
7 Укажите сумму моментов сил относительно точки А?
|
М+q ∙ 2- RВ∙2 |
-М + q ∙ 2 - - RВ ∙ 2 |
М - q ∙ 2 + + RАY ∙ 2 |
М + q ∙ 2+ + RАY ∙ 2 |
|
8 Укажите сумму проекции сил на ось Х?
|
RАХ |
-RАХ |
0 |
RАХ +RАY- -q ∙ 2 + RВ |
|
9 Укажите сумму проекции сил на ось Y?
|
RАY - q ∙ 2 |
RАY - q ∙ 2 + + RВ |
q ∙ 2 |
RАY + RВ |
|
10 Укажите сумму моментов сил относительно точки В?
|
М - q ∙ 2+ + RАY ∙ 2 |
М + q ∙ 2- - RВ ∙ 2 |
-М + q∙2- RВ∙2 |
М + q ∙ 2 + + RАY∙2 |
Вариант 5
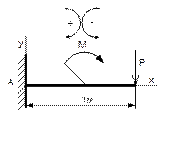
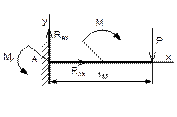
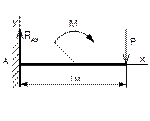
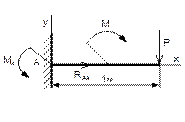
Рисунок 57 Рисунок 58 Рисунок 59 Рисунок 60
Таблица 17 – Определение опорной реакции заделки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции?
|
57 |
58 |
59 |
60 |
|
2 Сколько реакций дает жесткая заделка?
|
одну |
две |
три |
четыре |
|
3 Сколько уравнений равновесия надо составить для решения задачи?
|
∑ МА= 0 |
∑ FКХ = 0 ∑ FКY = 0 ∑ МА = 0 |
∑ FКХ = 0 ∑ FКY = 0 |
∑ FКХ = 0 ∑ FКY = 0 ∑ FКZ = 0 |
|
4 Чему равна проекция внешнего момента на ось Х?
|
МR |
-М |
М |
0 |
|
5 Чему равна проекция реактивного момента на ось Y?
|
М R |
-М R |
0 |
М |
|
6 Чему равен реактивный момент относительно точки А?
|
М R |
-М R |
0 |
-М |
|
7 Чему равен момент силы Р относительно точки А?
|
RАY – Р |
Р∙1 |
0 |
RАY∙1 |
|
8 Укажите сумму проекций сил на ось Х?
|
RАY – Р |
Р |
-RАХ |
RАХ |
|
9 Укажите сумму проекций сил на ось Y
|
RАY - Р |
-RАY - Р |
RАY |
-Р |
|
10 Укажите сумму моментов сил относительно точки А?
|
-М R + М +Р |
М R+ М + Р |
-М R + М – Р |
М R |
Вариант 6
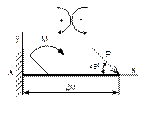
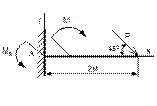
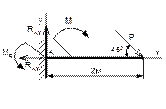
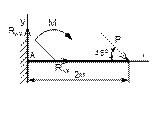
Рисунок 61 Рисунок 62 Рисунок 63 Рисунок 64
Таблица 18– Определение опорной реакции заделки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции? |
61 |
62 |
63 |
64 |
|
2 Какие уравнения равновесия надо составить для определения реакций? |
∑ FКХ = 0 ∑ FКY = 0 ∑ МА = 0 |
∑ FКХ = 0 ∑ FКY = 0 |
∑ FКХ = 0 ∑ FКY = 0 ∑ FКZ = 0 |
∑ МА = 0 |
|
3 Чему равна проекция внешнего момента на ось Х? |
М |
-М |
0 |
М R |
|
4 Чему равна проекция силы Р на ось Х?
|
-Р ∙ cos 450 |
Р ∙ cos 450 |
0 |
-Р ∙ sin 450 |
|
5 Чему равна проекция силы Р на ось Y? |
Р∙cos 450 |
0 |
Р∙sin 450 |
-Р∙sin 450 |
|
6 Чему равен момент силы Р относительно точки А? |
Р∙sin 450∙2 |
-Р∙sin 450∙2 |
Р∙cos 450∙2 |
-Р∙cos 450∙2 |
|
7 Чему равен реактивный момент относительно точки А? |
М |
-М R |
М R |
0 |
|
8 Укажите сумму проекций сил на ось Х?
|
RАХ + + Р ∙ cos450 |
-RАХ+ Рsin450 |
RАХ –Рcos450 |
Рcos450–RАХ |
|
9 Укажите сумму проекций сил на ось Y? |
-RАY – Рsin450 |
RАY |
RАY – Рsin450 |
-Р cos 450 |
|
10 Укажите сумму моментов сил относительно точки А?
|
МR+М + +Р∙sin450∙2 |
-МR + М + +Р∙sin450∙2 |
МR + М |
М - Р∙sin450∙2 |
Вариант 7
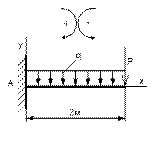
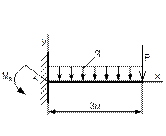
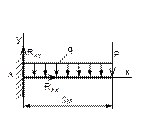
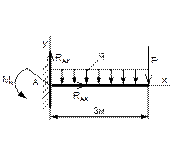
Рисунок 65 Рисунок 66 Рисунок 67 Рисунок 68
Таблица 19– Определение опорной реакции заделки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции?
|
65 |
66 |
67 |
68 |
|
2 Сколько реакций дает жесткая заделка?
|
одну |
две |
Три |
четыре |
|
3 Сколько уравнений равновесия надо составить для решения задачи?
|
два |
четыре |
Одно |
три |
|
4 Какие уравнения равновесия надо составить для решения задачи?
|
∑ FКХ = 0 ∑ FКY = 0 ∑ FКZ = 0 |
∑ МА= 0 |
∑ FКХ = 0 ∑ FКY = 0 ∑ МА = 0 |
∑ FКХ = 0 ∑ FКY = 0 |
|
5 Чему равна проекция момента МR на ось Y?
|
М R |
-М R |
0 |
- |
|
6 Чему равна проекция силы Р на ось Х? |
Р∙sin 90 0 |
- Р∙ cos 0 0 |
0 |
- Р |
|
7 Чему равна проекция силы Р на ось Y?
|
- Р |
-Р∙ cos 0 0 |
Р∙ cos 0 0 |
Р∙sin 0 0 |
|
8 Чему равен момент силы Р относительно точки А? |
Р ∙ 3 |
-Р ∙ 3 |
Р |
- Р |
|
9 Укажите сумму проекций сил на ось Y?
|
RАY + q∙3 + Р |
RАY+ q∙3 - Р |
RАY- q∙3 +Р |
RАY - q∙3 -Р |
|
10 Укажите сумму моментов сил относительно точки А?
|
-М R+ q∙4,5+ +Р∙3 |
М R - q ∙ 4,5 |
М R + q ∙ 4,5 - -Р∙3 |
q ∙ 4,5 - Р |
Вариант 8
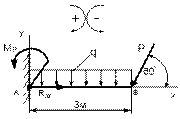
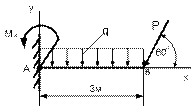
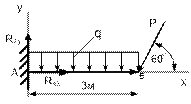
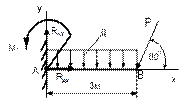
Рисунок 69 Рисунок 70 Рисунок 71 Рисунок 72
Таблица 20 – Определение опорной реакции заделки
|
Вопросы |
Ответы |
|||
|
1 |
2 |
3 |
4 |
|
|
1 Укажите на каком рисунке правильно нанесены реакции? |
69 |
70 |
71 |
72 |
|
2 Сколько реакций дает жесткая заделка?
|
одну |
две |
три |
четыре |
|
3 Сколько уравнений равновесия надо составить для решения задачи? |
два |
четыре |
одно |
три |
|
4 Какие уравнения равновесия надо составить для решения задачи?
|
∑ Fkх = 0 ∑ Fkу = 0 ∑ Fkz = 0 |
∑ МА= 0 |
∑ Fkх = 0 ∑ Fkу = 0 ∑ МА= 0 |
∑ Fkх = 0 ∑ Fkу = 0
|
|
5 Чему равна проекция момента МR на ось Y?
|
М R |
-М R |
0 |
- |
|
6 Чему равна проекция силы Р на ось Х?
|
Р ∙ sin 60 0 |
- Р ∙ cos 60 0 |
Р ∙ cos 60 0 |
- Р ∙ sin 600 |
|
7 7 Чему равна проекция силы Р на ось Y?
|
Р ∙ sin 60 0 |
- Р ∙ cos 60 0 |
Р ∙ cos 60 0 |
- Р ∙ sin 60 0 |
|
8 Чему равен момент силы Р относительно точки А?
|
Р ∙ 3 |
- Р∙ sin 60 0∙3 |
Р ∙ sin 60 0 ∙ 3 |
- Р ∙ cos 60 0∙3 |
|
9 Укажите сумму проекций сил на ось Y?
|
RАY + q ∙ 3 |
RАY + q ∙ 3 - -Р ∙ sin 60 0 |
RАY- q ∙ 3 - -Р ∙ in 60 0 |
-RАY- q∙3- -Р∙sin 60 0 |
|
10 Укажите сумму моментов сил относительно точки А?
|
- МR + q∙4,5 + +Р∙ sin 60 0∙3 |
М R- q ∙ 4,5 |
М R+ q ∙ 4,5 - -Р ∙ sin 60 0 ∙ 3 |
q ∙ 4,5 - sin60 0 |
8.3 Пример 1. Определение опорных реакций
двухопорной балки
Определить опорные реакции двухопорной балки в соответствии с рисунком 73, если F1 = 8 кН; F2 = 10 кН; q = 0,4 кН/м; М = 5 кН×м; а = 1,5 м; в = 2 м; с = 2 м.
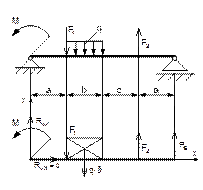
Рисунок 73
Решение
1 Освобождаем балку от связей (опор), заменив их опорными реакциями.
2 Выбираем расположение координатных осей, совместив ось х с балкой, а ось у направив перпендикулярно оси х.
3 Составляем уравнения равновесия статики и определяем неизвестные реакции опор.
Напомним, что для плоской системы параллельных сил достаточно двух уравнений равновесия
åМА= 0; åМВ = 0.
![]()
Rв = ![]()
Rв = ![]() кН
кН
![]()
RА = ![]()
RA =![]() кН
кН
Значение реакции опоры В получено со знаком «минус». Это означает, что RВ направлена вертикально вниз.
4 Проверка правильности найденных результатов
å Fку = RА – F1 – q b + F2 + RВ = 0
å Fку = 5,37 – 8 – 0,4 ∙ 2 + 10 – 6,57 = 0
5 Условие равновесия å Fку = 0 выполняется, следовательно, реакции опор RА и RВ найдены верно.
8.4 Пример 2. Определение опорных реакций заделки
Горизонтальная балка, поддерживающая балкон, подвергается действию
равномерно распределенной нагрузки интенсивностью q = 2 кН/м в соответствии с рисунком 74. На балку в точке С передается
нагрузка от колонны P = 2 кН; ![]() = 1,5
м. Определить реакции заделки А.
= 1,5
м. Определить реакции заделки А.
Решение
1 Освобождаем балку от опоры, заменив ее опорными реакциями.
2 Выбираем расположение координатных осей (рисунок 74).
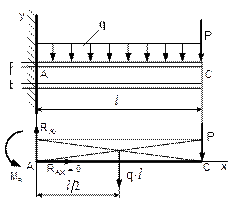
Рисунок 74
Решение
1 Освобождаем балку от опоры, заменив ее опорными реакциями.
2 Выбираем расположение координатных осей.
3 Применим условие равновесия плоской системы параллельных сил и составим два уравнения равновесия
å Fку = RАу – q ![]() - Р = 0;
RАу = q
- Р = 0;
RАу = q ![]() + Р ; RАу = 2 × 1,5 + 2 = 5 кН;
+ Р ; RАу = 2 × 1,5 + 2 = 5 кН;
åМА = - М R+ q ![]() + P
+ P ![]() = 0; М R
= q
= 0; М R
= q ![]() + P
+ P ![]() ;
;
МR = 2 ×![]() + 2
+ 2 ![]() = 5,25 кНм.
= 5,25 кНм.
Горизонтальная составляющая RАх = 0, так как горизонтальные активные силы отсутствуют.
4 Проверяем правильность найденных результатов.
åМ
С = - ![]() -
M R +
-
M R + ![]() = 0:
-
= 0:
- ![]() - 5,25 +
- 5,25 + ![]() = 0
= 0
5 Условие равновесия å М С = 0 выполняется, следовательно, реакции опоры найдены верно.
8.5 Задание 1 для бригад
Определить опорные реакции балки с шарнирно – неподвижной и шарнирно –подвижной опорами в соответствии с рисунком 75, если:
P = 10 кН; q = 10 кН / м; М = 20 кН×м; а = в = с = 2 м.
|
|
|
|
|
|
|
|
|
Рисунок 75
8.6 Задание 2 для бригад
Определить опорные реакции балки с одним жестко защемленным и другим свободным концом в соответствии с рисунком 76, если: P = 5 кН; q = 10 кН / м; М = 10 кНм; а = в = с = 1 м.
|
|
|
|
|
|
|
|
|
Рисунок 76
9 САМОСТОЯТЕЛЬНАЯ РАБОТА 4
Тема: Плоская система произвольно расположенных сил
Выполнение расчетно-графической работы 2.
После выполнения самостоятельной работы студент должен:
- иметь представление о плоской системе произвольно расположенных сил, об уравнениях равновесия, о видах нагрузок, о типах опор балочных систем, о реакциях в опорах;
- знать три формы уравнений равновесия и применение их при определении реакций в опорах;
- уметь определять реакции в опорах балочных систем, применяя уравнения равновесия, проверять правильность решения задач.
9.1 Рекомендуемая последовательность для выполнения расчетно-графической работы 2
1 Выделить тело, равновесие которого надо рассмотреть.
2 Изобразить расчетную схему: условно изобразить опоры и приложить заданные силы.
3 Отбросить опоры, а направление их реакций изобразить на схеме.
4 Провести оси координат так, чтобы одна ось была перпендикулярна некоторым неизвестным силам. Наметить центры моментов в точке пересечения линий действия двух неизвестных сил или на линии действия одной неизвестной силы.
5 Составить уравнения равновесия.
6 Решить уравнения равновесия и определить неизвестные силы.
7 Проверить правильность решения по уравнению равновесия, которое не было использовано.
9.2 Задание для самостоятельной работы 4
Задача 1 Определить реакции жесткой заделки в соответствии с рисунком 77. Данные своего варианта взять из таблицы 21
Задача 2. Определить реакции опор двухопорной балки в соответствии с рисунком 78. Данные своего варианта взять из таблицы 22.
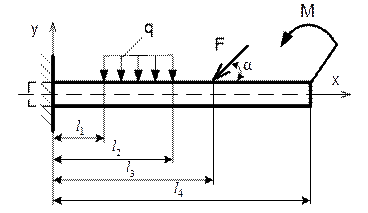
Рисунок 77– Схема для выполнения задачи 1
Таблица 21 – Данные для выполнения задачи 1
|
Вариант |
Вес балки, G |
Интенсивность распределен- ной нагрузки, q |
Мо-мент, М |
Сила, F |
Угол наклона, α |
Длина, м |
|||
|
Н |
Н/м |
Н×м |
Н |
град |
|
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
5 6 7 8 9 10 10 9 8 7 6 5 5 6 7 8 9 10 10 9 8 7 6 5 5 6 7 8 9 9 |
2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 4 4 3 3 3 3 3 3 2 2 2 2 3 |
4 4 4 4 4 3 3 3 3 3 5 5 5 5 5 5 6 6 6 6 6 6 5 5 5 5 3 3 3 4 |
6 6 6 6 6 6 8 8 8 8 8 8 6 6 6 6 8 8 8 8 8 8 6 6 6 6 8 8 8 6 |
20 40 65 25 50 15 35 70 20 40 55 75 50 40 35 25 20 80 80 50 15 25 20 40 35 55 20 50 80 40 |
1 2 3 4 4 3 2 1 3 4 3 2 1 2 1 2 2 1 3 1 2 3 1 2 1 2 2 2 1 1 |
3 3 5 5 5 5 5 3 4 5 5 5 4 3 2 3 5 4 5 2 3 5 5 3 2 5 5 5 2 2 |
1 2 3 4 5 6 7 8 8 7 6 5 4 3 2 1 2 3 4 5 6 7 8 8 7 6 5 4 3 3 |
6 6 8 10 10 10 10 12 12 10 10 10 6 5 5 5 6 5 6 8 9 8 10 9 8 10 6 6 4 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 22 – Данные для выполнения задачи 2
|
Схема в соответствии с рисунком 78 |
Вариант |
Интенсивность распределенной нагрузки, q |
Сила, F |
Момент, М |
|
Н/м |
Н |
Н×м |
||
|
1
|
11 22 30 |
2 10 1,5 |
25 16 50 |
20 14 30 |
|
2 |
01 12 23 |
1 4,5 2 |
60 20 15 |
54 85 40 |
|
3 |
02 13 24 |
5 2,5 4 |
80 15 30 |
25 10 20 |
|
4 |
03 14 25 |
4 1 12 |
10 12 16 |
8 10 15 |
|
5 |
04 15 26 |
5 4,5 8 |
50 35 25 |
35 30 20 |
|
6 |
05 16 27 |
8 3,5 0,5 |
12 10 8 |
20 45 10 |
|
7 |
06 17 28 |
2 4 6 |
50 10 12 |
35 5 8 |
|
8 |
07 18 29 |
4 6,5 10 |
18 24 16 |
15 20 12 |
|
9 |
08 19 20 |
4 1,5 1 |
15 40 20 |
2 15 18 |
|
10 |
09 10 21 |
4 6 2 |
50 65 80 |
10 8 100 |
9.3 Контрольные вопросы
а) главный момент и главный вектор системы сил равны нулю. Можно ли утверждать, что система сил находится в равновесии ?
б) как должна быть направлена ось Ох относительно прямой, проходящей через точку А и В, если уравнения равновесия имеют вид
å М А = 0;
å М В = 0;
å F ку = 0?
1) ось Ох перпендикулярна АВ;
2) ось Ох не перпендикулярна АВ;
в) как должна быть расположена точка А, относительно которой алгебраическая сумма моментов всех сил равна нулю, если уравнения равновесия имеют вид : å F кх = 0; å F ку = 0; å М А = 0 ?
1) точка А может быть расположена в любом месте плоскости
действия сил;
2) точка А может быть точкой пересечения осей Ох и Оу;
г) могут ли точки А, В и С располагаться на одной прямой, если в качестве уравнений равновесия приняты уравнения
åМ А = 0;
åМ В = 0;
åМ С = 0 ?
д) сколько независимых уравнений равновесия можно составить для плоской системы параллельных сил ?
1) одно уравнение равновесия;
2) два уравнения равновесия;
3) три уравнения равновесия;
е) перечислите типы опор балок и виды нагрузок;
ж) можно ли утверждать, что тело находится в равновесии под действием произвольной системы сил, если известно только, что относительно одной из его точек сумма моментов равна нулю (рассматриваемое тело не является рычагом)?
з) почему в шарнирных опорах балок возникает только реактивные силы, а в заделке, кроме того, и реактивный момент ?
9.4 Литература: [2] c.45-50; [3] c.35-40; [9] c.44-49.
10 САМОСТОЯТЕЛЬНАЯ РАБОТА 5
Тема: Пространственная система сил
Изучение вопроса «Момент силы относительно оси».
После выполнения самостоятельной работы студент должен:
- иметь представление о пространственных системах сил и их действии на тело:
- знать условие равновесия и уравнения равновесия для пространственной системы сил, момент относительно оси.
10.1 Задание для самостоятельной работы
Изучить теоретический материал и составить конспект, раскрывая следующие понятия:
а) момент силы относительно оси (обозначение, модуль, знак, единица измерения);
б) условие равновесия;
в) шесть уравнений равновесия пространственной системы сил (без вывода).
10.2 Контрольные вопросы
а) момент силы относительно оси равен нулю:
1) когда сила параллельна оси;
2) когда линия действия сил пересекает ось;
3) когда сила и ось расположены в одной плоскости.
б) по каким формулам определяются главный вектор и главный момент пространственной системы сил?
в) вставьте пропущенные слова:
1) для определения момента силы относительно оси нужно ... силу на плоскость, ... оси, и найти момент проекции силы относительно точки ... оси с плоскостью.
2) геометрическая сумма всех сил данной пространственной системы называется главным ……
10.3 Литература: [2] c.55 - 60, 63 - 67; [3] c.40 - 41; [9] c.51 - 59.
11 ЛАБОРАТОРНАЯ РАБОТА 1
Тема: Определение центра тяжести плоских фигур
После выполнения лабораторной работы студент должен:
- знать методы определения центра тяжести тела; формулы для определения положения центра тяжести плоских фигур;
- уметь определять положение центра тяжести плоских фигур.
11.1 Теоретическое обоснование
Центром тяжести называется точка, через которую проходит линия действия силы тяжести, т.е. точка, являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела.
Определение положения центра тяжести имеет важное практическое значение, так как относительно этой точки данное тело находится в условии равновесия.
В инженерных задачах часто приходится определять центры тяжести различных сечений тел, представляющих собой геометрические плоские фигуры иногда весьма сложной формы. При определении координат центра тяжести площади, сложную фигуру разбивают на возможные меньшее число простых фигур и определяют координаты их центров тяжести в заданной системе координат. Координаты центра тяжести всей фигуры Хс и Ус определяют по формулам:
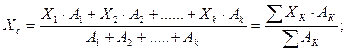
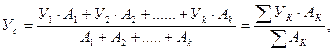
где Х 1, Х 2….Х k - расстояние от оси У до центра тяжести простой фигуры , мм;
У 1, У 2….У k - расстояние от оси Х до центра тяжести простой фигуры , мм;
А 1, А 2….А k - площадь простой фигуры, мм 2.
Если сложная фигура имеет отверстие в виде геометрических фигур, то эти площади необходимо ввести в формулу со знаком «минус». Этот метод называется методом отрицательных площадей.
Положение центра тяжести некоторых простых фигур:
а) прямоугольник, квадрат, параллелограмм - центр тяжести этих фигур находится в точке пересечения их диагоналей;
б) центр тяжести треугольника лежит на пересечении медиан и отстоит от
основания его на расстоянии ![]() ;
;
в) центр тяжести полукруга в соответствии с рисунком 79 определяют по формуле
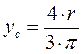 ;
хс = 0
;
хс = 0
Рисунок 79
г) центр тяжести сегмента круга (рисунок 80) определяют по формуле
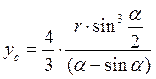 ;
; ![]() ,
,
где a - центральный угол сегмента, рад.
Рисунок 80
д) центр тяжести кругового сектора (рисунок 81) определяют по формуле
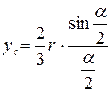 ;
; ![]() ,
,
где a - центральный угол сектора, рад.
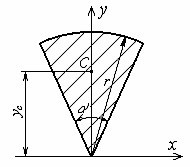
Рисунок 81
Рисунок 82
Статический момент площади выражается единицами длины в третьей степени, например: мм 3.
Понятие о статическом моменте площади облегчает решение задач по определению координат центра тяжести сложных фигур.
Определение координат центра тяжести фигуры через статические моменты площади:
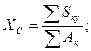 ;
; 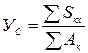 .
.
Если начало координат поместить в центре тяжести площади, то статические моменты площади относительно осей Ох и Оу будут равны нулю, так как y c = 0 и x c = 0.
Рассмотрим определение центра тяжести однородной плоской фигуры, имеющую сложную форму (рисунок 83). Ее можно разбить на три простых фигуры: 1 – прямоугольник; 2 – круг; 3 – треугольник.
Проводя систему координат хОу, для каждой фигуры определяем координаты центра тяжести и площади простых фигур:
х 1 =
![]() = 15,5 см; у 1 = 0; А1 = 31× 12 = 372 см2;
= 15,5 см; у 1 = 0; А1 = 31× 12 = 372 см2;
х 2 = 8 см; у2 = 0; А2 = - ![]() ; А2 = -
; А2 = - ![]() = - 78,5
см2,
= - 78,5
см2,
знак «минус» показывает, что это площадь отверстия.
х 3 = 13 + ![]() = 13 + 8 = 21 см; у3 = 0; А3 = -
= 13 + 8 = 21 см; у3 = 0; А3 = - ![]() = - 54
см2,
= - 54
см2,
знак «минус» у площади показывает, что это площадь отверстия.
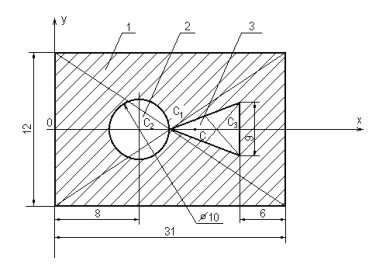
Рисунок 83
Определим координаты центра тяжести всей фигуры.
![]()
![]() см;
см; ![]() .
.
11.2 Схема и описание лабораторной установки
Установка для опытного определения координат центра тяжести способом подвешивания (рисунок 84) состоит из вертикальной стойки 1, к которой прикреплена игла 2. Плоская фигура 3 изготовлена из картона, жести или другого материала, в которой можно легко проколоть отверстие. Отверстие А и В прокалываются в произвольно расположенных точках (лучше на наиболее удаленном расстоянии друг от друга).
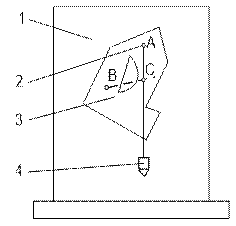
1 – вертикальная стойка;
2 – игла;
3 – плоская фигура;
4 – отвес.
Рисунок 84 – Лабораторная установка
При помощи отвеса 4, закрепленного на той же игле, на фигуре прочерчивают линию, соответствующую линии отвеса. Центр тяжести С фигуры будет находиться в точке пересечения вертикальных линий, нанесенных при подвешивании фигуры в точках А и В.
11.3 Порядок выполнения работы
а) прочитать теоретическое обоснование лабораторной работы;
б) ознакомиться с устройством лабораторной установки для определения центра тяжести плоской фигуры;
в) в соответствии с заданием начертить чертеж фигуры сложной формы в масштабе МL = 1мм /мм и проставить ее размеры (рисунок 85). Исходные данные взять из таблицы 23;
г) провести оси координат так, чтобы они охватывали всю фигуру;
д) разбить сложную фигуру на простые части, определить площадь и координаты центра тяжести каждой простой фигуры относительно выбранной системы координат. Данные необходимо записать в таблицу 24;
е) вычислить координаты центра тяжести всей фигуры аналитическим способом и показать на чертеже центр тяжести плоской фигуры С;
ж) вырезать данную фигуру из тонкого картона или фанеры. Просверлить два отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры;
з) подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадавшую с нитью отвеса. То же повторить при подвешивании фигуры в другой точке. Сделать отверстие в точке пересечения проведенных линий – центре тяжести фигуры;
и) совместить пластинку (фигуру) с чертежом на бумаге (выполненные в одинаковом масштабе). Центр тяжести фигуры С, найденный аналитическим способом, и центр тяжести, найденный опытным путем, должны совпадать.
11.4 Варианты заданий
Вычислить координаты центра тяжести плоской сложной фигуры. Исходные данные необходимые для выполнения лабораторной работы своего варианта необходимо выбрать в соответствии с рисунком 85 и из таблицы 23
а) б) в)
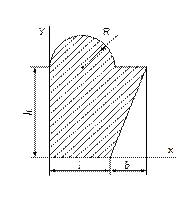
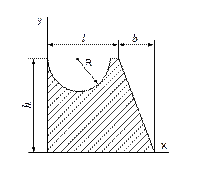
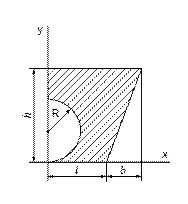
Рисунок 85 - Схемы для выполнения лабораторной работы 1
Примечание - Данные задачи следует выбрать в следующем порядке:
- рисунок 85, а – варианты 1 – 10;
- рисунок 85, б – варианты 11 – 20;
- рисунок 85, в – варианты 21 – 30.
Например: вариант 1 - рисунок 85, а, данные из столбика 1 таблицы 23;
вариант 15 - рисунок 85, б, данные из столбика 5 таблицы 23 и т.д.
Таблица 23 - Исходные данные
|
Размеры,мм |
Вариант |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
R |
10 |
20 |
10 |
25 |
30 |
28 |
24 |
22 |
18 |
16 |
|
H |
50 |
60 |
40 |
80 |
70 |
90 |
60 |
50 |
60 |
40 |
|
|
60 |
50 |
50 |
60 |
60 |
80 |
70 |
80 |
80 |
60 |
|
|
20 |
10 |
10 |
20 |
20 |
30 |
40 |
30 |
30 |
40 |
11.5 Отчет о работе
Тема: Определение центра тяжести плоских фигур.
Цель работы: Определить центр тяжести сложной фигуры аналитическим и опытным способами.
Оборудование и принадлежности: Лабораторная установка, картонная бумага, ножницы, чертежные принадлежности, вычислительная машинка.
Ход работы
1 Начертим фигуру сложной формы в масштабе МL = 1 мм / мм и разбиваем на простые фигуры.
2 Определяем площадь и координаты центра тяжести каждой простой фигуры относительно выбранной системы координат и данные записываем в таблицу 24.
Таблица 24 - Результаты вычислений
|
Простые фигуры |
А К , мм ² |
Х к , мм |
Ук , мм |
|
|
|
|
|
Вычисляем координаты центра тяжести всей фигуры (положение центра тяжести С нанести на чертеж фигура) по формулам
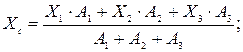
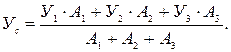
4 Определяем центр тяжести данной фигуры выполненной из картона или фанеры путем подвешивания в двух точках на лабораторной установке и находим Хс (опыт) и Ус (опыт).
5 Совмещаем пластинку (фигуру) с чертежом на бумаге выполненные в одинаковом масштабе.
6 Вывод.
7 Ответы на контрольные вопросы.
11.6 Контрольные вопросы
а) можно ли рассматривать силу тяжести тела как равнодействующую системы параллельных сил?
б) может ли располагаться центр тяжести вне самого тела?
в) в чем сущность опытного определения центра тяжести плоской фигуры?
г) как определяется центр тяжести сложной фигуры, состоящей из нескольких простых фигур?
д) как следует рационально производить разбиение фигуры сложной формы на простые фигуры при определении центра тяжести всей фигуры?
е) какой знак имеет площадь отверстия в формуле для определения центра тяжести?
ж) на пересечении каких линий треугольника находится его центр
тяжести?
з) если фигуру трудно разбить на небольшое число простых фигур, какой способ определения центра тяжести может дать наиболее быстрый ответ?
12 САМОСТОЯТЕЛЬНАЯ РАБОТА 6
Тема: Центр тяжести
Выполнение расчетно-графической работы 3.
После выполнения самостоятельной работы студент должен:
- иметь представление о системе параллельных сил и ее действии на тело, о центре системы параллельных сил, о силе тяжести и центре тяжести;
- знать методы определения центра тяжести тел, формулы для определения положения центра тяжести плоских фигур;
- уметь определять положение центра тяжести фигур, составленных из стандартных профилей проката; работать со справочной литературой.
12.1 Рекомендуемая последовательность для выполнения
расчетно-графической работы 3
а) обозначить фигуры номерами и выписать из таблиц ГОСТов необходимые данные:
1) для швеллера А - ГОСТ 8240 - 72;
2) для уголка равнополочного В - ГОСТ 8509 - 72;
3) для двутавра С - ГОСТ 8239 - 72;
4) для уголка неравнополочного Д - ГОСТ 8510 - 72;
б) определить координаты центра тяжести каждой фигуры относительно заданных осей координат;
в) определить положение центра тяжести составного сечения.
12.2 Задание для самостоятельной работы
Определить положение центра тяжести сечения, составленного из стандартных профилей проката в соответствии с рисунками 86,87,88
Примечание – Данные своего варианта следует выбрать в следующем порядке: рисунок 86 – варианты 1...10; рисунок 87 – варианты 11...20, и т.д.
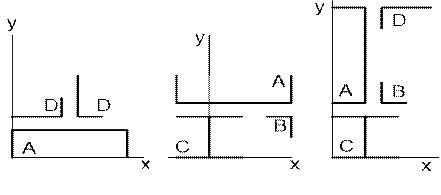
Рисунок 86 Рисунок 87 Рисунок 88
Таблица 25 – Данные для выполнения расчетно-графической работы 3
|
Вариант |
А – швеллер |
В – уголок равнополочный |
С – двутавр |
D – уголок неравнополочный |
|
1 |
18 |
90 х 90 х 9 |
10 |
125 х 80 х 7 |
|
2 |
16 |
70 х 70 х 5 |
12 |
100 х 63 х 6 |
|
3 |
12 |
63 х 63 х 6 |
14 |
80 х 50 х 5 |
|
4 |
14 |
75 х 75 х 8 |
16 |
125 х 80 х 10 |
|
5 |
14а |
80 х 80 х 6 |
20 |
110 х 70 х 8 |
|
6 |
16а |
80 х 80 х 6 |
22 |
160 х 100 х 12 |
|
7 |
22 |
110 х 110 х 8 |
24 |
180 х 110 х 12 |
|
8 |
18 |
90 х 90 х 8 |
30 |
90 х 56 х 8 |
|
9 |
20а |
100 х 100 х 12 |
30а |
140 х 90 х 10 |
|
10 |
30 |
140 х 140 х 10 |
40 |
250 х 160 х 10 |
12.3 Контрольные вопросы
а) является ли центр тяжести тела центром параллельных сил?
б) как располагается центр тяжести, если тело имеет ось симметрии?
в) как определяется центр тяжести сложной фигуры, состоящей из нескольких простых фигур?
г) какой знак имеет площадь отверстия в формуле для определения центра тяжести?
д) тело имеет две плоскости симметрии, где лежит центр тяжести тела?
е) как определяется центр тяжести полукруга, сектора, сегмента?
ж) как определяется площадь и положение центра тяжести стандартных профилей проката (уголок, швеллер, двутавр)?
12.4 Литература: [2] c.67 - 81; [3] c.42 - 48; [9] c.60 - 65.
13 САМОСТОЯТЕЛЬНАЯ РАБОТА 7
Тема: Кинематика точки
Выполнение расчетно-графической работы 4.
После выполнения самостоятельной работы студент должен:
- иметь представление о скоростях средней и истинной, об ускорении при прямолинейном и криволинейном движениях, о различных видах движения точки;
- знать формулы скоростей и ускорений точки (без вывода), определение величины и направления скорости и ускорения точки, частные случаи движения точки и их уравнения;
- уметь определять кинематические параметры движения точки.
13.1 Рекомендуемая последовательность для выполнения
расчетно-графической работы 4
а) определить уравнение траектории точки,исключая из уравнений движения параметр время;
б) определить проекции скорости Vx ,Vy и
ускорения ![]() ,
, ![]() (дифференцировать
уравнения движения);
(дифференцировать
уравнения движения);
в) определить модуль и направление полной скорости точки;
![]()
![]() V =
V = ![]()
![]()
г) определить модуль ускорения точки а;
![]()
д) вычислить модули касательного а t и нормального ускорений а n точки:
![]() ;
; ![]()
е) вычислить
радиус кривизны точки: ![]()
13.2 Задание для самостоятельной работы 7
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t 1 (c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения и радиус кривизны. Данные своего варианта взять из таблицы 26.
Таблица 26 – Данные для выполнения расчетно-графической работы 4
|
Вариант |
Уравнения движения, см |
Время, с |
|
|
x = х (t) |
y = y (t) |
t1 |
|
|
1 |
- 2 × t 2 + 3 |
- 5 × t |
0,5 |
|
2 |
4 × t + 4 |
- 4 / (t + 1) |
2 |
|
3 |
3 × t 2 + 2 |
- 4 × t |
0,5 |
|
4 |
3 × t 2 - t + 1 |
5 t 2 - 5 × t / 3 - 2 |
1 |
|
5 |
- 3 / (t + 2) |
3 × t + 6 |
2 |
|
6 |
- 4 × t 2 + 1 |
- 3 × t |
0,5 |
|
7 |
- 2 × t - 2 |
- 2 / (t + 1) |
2 |
|
8 |
3 × t |
4 × t 2+1 |
0,5 |
|
9 |
- 5 × t 2 - 4 |
3 × t |
1 |
|
10 |
2 - 3 × t - 6 × t 2 |
3 - 3 × t /2 - 3 × t 2 |
0 |
|
11 |
7 × t 2 - 3 |
5 × t |
0,25 |
|
12 |
3 - 3 × t 2 + t |
4 - 5 × t 2 + 5 × t /3 |
1 |
|
13 |
- 6 × t |
- 2 × t 2 – 4 |
1 |
|
14 |
- 4 × t 2 + 1 |
- 3 × t |
1 |
|
15 |
5 × t 2 + 5 × t / 3-3 |
3 × t 2 + t + 3 |
1 |
|
16 |
2 × t |
(t + 1) 2 |
2 |
|
17 |
4 + 2 × t 2 |
4 - 2 × t |
1 |
|
18 |
3 × t |
-5 × t 2 - 4 |
2 |
|
19 |
2 × t + 2 |
(t + 1) 3 |
1 |
|
20 |
- 2 × t |
2 × t 2 - 2 |
1 |
|
21 |
2 × t + 4 |
2 × t 2 – 2 |
1 |
|
22 |
t + 3 |
2 / (t + 3) |
1 |
|
23 |
- 4 ×cos π / 3 × t |
- 2 ×sin π / 3 × t |
1 |
|
24 |
2 × sin π / 8× t |
- 3× cos π / 8 × t + 4 |
1 |
|
25 |
- 4 × cos (π× t / 3) |
- 2× sin (π × t / 3) - 3 |
1 |
|
26 |
4 × cos (π × t / 3) |
- 3× sin (π × t / 3) |
1 |
|
27 |
4×cos 2 (π× t / 3) +2 |
4× sin 2 (π ×t / 3) |
1 |
|
28 |
- cos (π× t 2 / 3) + 3 |
sin × (π × t 2 / 3) - 1 |
1 |
|
29 |
5 × sin 2 (π × t / 6) |
- 5 × cos 2 (π × t / 6) - 3 |
1 |
|
30 |
5 × cos (π × t 2 / 3) |
- 5 × sin (π × t 2 / 3) |
1 |
13.3 Контрольные вопросы
а) что изучает раздел «Кинематика»?
б) что такое система отсчета?
в) как формулируется закон движения точки и какими способами его можно задать?
г) что называется скоростью равномерного движения точки? что она характеризует?
д) как определить среднюю скорость движения точки?
е) как направлен вектор скорости точки при криволинейном движении?
ж) как определить нормальное и касательное ускорения точки?
з) как движется точка, если:
1) an = 0, at = 0;
2) an = 0, at ≠ 0;
3) an ≠ 0, at = 0;
4) an ≠ 0, at ≠ 0;
и) имеет ли ускорение точка, равномерно движущаяся по криволинейной траектории?
к) что такое график перемещения, график скорости движения точки?
л) при каком способе задания движения точки необходимо дополнительно указать ее траекторию?
13.4 Литература: [2] c.87 - 98; [3] c.128 - 136; [9] c.66 - 78.
14 САМОСТОЯТЕЛЬНАЯ РАБОТА 8
Тема: Простейшие движения твердого тела
Решение задачи.
После выполнения самостоятельной работы студент должен:
- иметь представление о поступательном движении, его особенностях и параметрах; о вращательном движении тела и его параметрах;
- знать законы движения при поступательном и вращательном движениях, различные виды поступательного и вращательного движений твердого тела, формулы для определения параметров поступательного и вращательного движений тела.
14.1 Задание для самостоятельной работы 8
Определить параметры движения твердого тела.
Задание (смотри ниже) взять в соответствии со своим вариантом по журналу.
Задача 1. Тело, находящееся в покое, начало прямолинейное поступательно движение с ускорением 2м /с2. Приобретя скорость v = 10м / с, тело стало двигаться равномерно по дуге окружности радиуса r = 8м. Через 15 с равномерного движения тело внезапно остановилось.
Определить:
а) путь, пройденный телом за время его движения;
б) среднюю скорость на этом пути;
в) ускорение тела при движении по дуге окружности.
Задача 3. Тело движется равномерно поступательно по дуге окружности радиуса r = 200 м. Пройдя 150 м за 10 с. тело стало двигаться равнозамедленно и остановилось через 40 с после начала равнозамедленного движения.
Определить:
а) путь, пройденный телом за время движения;
б) ускорение тела в момент t = 24 с после начала равнозамедленного движения;
в) на каком расстоянии находилось тело в этот момент от места начала движения.
Задача 4. Тело при равнозамедленном вращении с угловым ускорением ε = - 2 рад / с2 в течение 1,4 мин сделало 2100 оборотов.
Определить:
а) угловую скорость тела в начале и в конце равнозамедленного
вращения;
б) скорость и нормальное ускорение точек тела в момент t = 60 с после
начала равнозамедленного вращения, если эти точки расположены на
расстоянии r = 0,5 м от оси вращения тела.
Задача 5.Тело двигалось равномерно поступательно со скоростью 2 м/с в течении 10 с, а затем, получив ускорение, двигалось равноускоренно еще 10 с, успев пройти за это все время (20 с) 90 м. С начала 91- го метра тело снова стало двигаться равномерно с той скоростью, которую приобрело к этому моменту. Через 10 с равномерного движения тело внезапно остановилось.
Определить:
а) весь путь, пройденный телом за 30 с;
б) ускорение тела в момент t = 15 с, считая от начала движения, если в
этот момент движение происходит по дуге окружности радиуса r = 20 м.
Задача 6. Ротор при угловой скорости n 0 = 720 об/мин начал равноускоренное вращение с угловым ускорением ε = 20 рад/ с2. После 12 с равноускоренного вращения ротор в течение 420 с вращается равномерно.
Определить:
а) угловую скорость равномерного вращения,
б) сколько оборотов совершил ротор за все рассмотренное в задаче время.
Задача 7. Тело двигалось равномерно поступательно в течение 20 с и прошло путь 100 м. В начале 21 - й секунды скорость тела внезапно возросла до 8 м / с, и с этой скоростью тело двигалось еще 20 с, а затем последовало равнозамедленное движение и через 20 с тело остановилось.
Определить:
а) весь путь, пройденный телом;
б) построить графики перемещения, скорости и ускорения тела, считая
движение тела прямолинейным.
Задача 8. В течение 15 с вращение вала происходило согласно уравнению:
φ = 20· t + 0,5 · t 3,
где φ – угол поворота, рад;
t – время, с.
Определить:
а) угловую скорость вала в момент t 0 = 0 с и t 1 = 15 с;
б) угловое ускорение в эти же моменты;
в) сколько оборотов совершил вал за 15 с.
Задача 9. Тело начало прямолинейное поступательное движение из состояния покоя с ускорением 0,8 м / с 2. Через 15 с после начала движения тело стало двигаться равнозамедленно и за последующие 20 с его скорость уменьшилась до 6 м/с и с этой скоростью тело двигалось еще 20 с и остановилось. Написать уравнения, которым подчинялось движение тела на каждом этапе; построить графики перемещения, скорости и ускорения тела.
Задача 10. Поступательное движение тела по окружности радиуса r =1 м подчиняется уравнению:
s =- 2 · t + 0,5 · ۠t 2,
где s – путь, м,
t – время, с.
Построить графики перемещения, скорости и касательного ускорения тела для первых шести секунд движения. На основании анализа графиков указать: в течение какого времени движение было ускоренным и в течение какого – замедленным, какой путь прошло тело за 6 с и успело ли оно пройти окружность полностью.
Задача 11. Тело начало равноускоренное поступательное движение из состояния покоя по прямой и через 5 с приобрело скорость v = 10 м/с
С этого момента тело начало двигаться по окружности радиуса r = 50 м. Двигаясь по окружности, тело первые 15 с совершало равномерное движение, затем в течение 10 с двигалось равнозамедленно до остановки. Определить:
а) среднюю скорость движения тела на всем пути;
б) значение полного ускорения тела через 5 с после начала равнозамедленного движения.
Задача 12. Шкив диаметром d = 400 мм в течение 10 с вращался с постоянной угловой скоростью ω 0 = 8 рад / с. Затем стал вращаться равноускоренно и через 12 с равноускоренного вращения его угловая скорость достигла ω 1 = 14 рад / с.
Определить:
а) число оборотов и среднюю угловую скорость за все время вращения;
б) окружную скорость точек, расположенных на ободе шкива, через 6 с
после начала равноускоренного движения.
Задача 13. Тело начало двигаться равноускоренно поступательно из состояния покоя по окружности радиусом r = 100 м и через 10 с приобрело скорость v = 20 м / с. С этого момента тело 15 с двигалось равномерно по окружности, после чего стало двигаться по прямой и через 5 с равнозамед - ленного движения по прямой остановилось.
Определить:
а) среднюю скорость движения тела на всем пути;
б) значение полного ускорения тела через 5 с после начала движения.
Задача 14. Вал диаметром d = 500 мм в течение 5 с вращался с постоянной угловой скоростью ω 0 = 20 рад / с, после чего стал замедлять свое вращение с постоянным угловым ускорением. Через 10 с после начала равнозамедленного вращения угловая скорость вала стала ω1 = 10 рад / с.
Определить:
а) число оборотов и среднюю угловую скорость вала за все время
вращения;
б) окружную скорость точек, расположенных на поверхности вала, через
4 с после начала равнозамедленного вращения.
Задача 15. Тело начало двигаться равноускоренно поступательно по дуге окружности радиусом r = 50 м из состояния покоя и через 20 с приобрело скорость v = 20 м / с. С этого момента тело стало двигаться прямолинейно, причем первые 5 с равномерно, а последующие 5 с – равнозамедленно до остановки.
Определить:
а) среднюю скорость движения тела на всем пути;
б) значение полного ускорения тела через 10 с после начала его
движения.
Задача 16. Тело, замедляя вращение с постоянным угловым ускорением ε = 2 рад / с 2 , через 14 с снизило свою угловую скорость до величины ω =12 рад / с, после чего вращалось равномерно с этой угловой скоростью в течение 10 с.
Определить:
а) число оборотов и среднюю угловую скорость за все время вращения;
б) окружную скорость точек тела, расположенных на расстоянии r = 1м
его оси вращения за 4 с до начала равномерного вращения.
Задача 17. Первые 5 с тело двигалось равномерно поступательно по окружности радиусом r = 50 м со скоростью v = 20 м / с. В последующие 10 с, двигаясь равнозамедленно по той же окружности, снизила свою скорость до 10 м /с и с этой скоростью тело начало равнозамедленно двигаться по прямой до полной остановки.
Определить:
а) среднюю скорость движения тела на всем пути;
б) полное ускорение тела после начала равнозамедленного движения.
Задача 18. Ротор диаметром d = 200 мм начал вращение из состояния покоя с постоянным угловым ускорением ε = 4 рад /с 2 и через некоторое время достиг угловой скорости ω = 40 рад / с, после чего с этой угловой скоростью сделал 510 оборотов.
Определить:
а) число оборотов и среднюю угловую скорость за все время вращения;
б) окружную скорость точек, расположенных на поверхности ротора,
через 8 с после начала вращения.
Задача 19. Тело начало равноускоренное поступательное движение из состояния покоя по прямой, прошло путь в 100 м и приобрело скорость v = 20 м / с. С этой скоростью тело продолжало прямолинейное движение в течение 5 с. После этого тело начало двигаться по окружности радиусом r = 40 м и течение 20 с двигалось равнозамедленно до полной остановки.
Определить:
а) среднюю скорость движения тела на всем пути;
б) полное ускорение тела через 10 с после начала его равнозамедленного
движения по окружности.
Задача 20. Двигатель, ротор которого вращался с частотой 430 об/мин, был отключен от источника питания и через 40 с снова подключен к источнику тока. За это время при равнозамедленном вращении ротора его угловая скорость снизилась до 5 рад / с. После подачи электроэнергии ротор двигателя, вращаясь равноускоренно, через 10 с снова приобрел частоту вращения 430 об/мин.
Определить:
а) число оборотов и среднюю угловую скорость за все время
равнозамедленного и равноускоренного вращения ротора двигателя;
б) окружную скорость точек, расположенных на поверхности ротора
через 30 с после отключения источника тока, если диаметр ротора 200 мм.
Задача 21. Ротор электромотора вращается с частотой 2700 об/мин. После выключения он делает до остановки 675 оборотов. Считая вращение ротора электромотора равнозамедленным, найти время вращения ротора с момента выключения до полной остановки Δ t, а тaк же угловые скорость и ускорение его в период торможения.
Задача 22. Маховик диаметром d = 1,5 м, начав равноускоренное вращение из состояния покоя, за Δt = 10 мин приобрел частоту вращения n =80об / мин. Определить окружную скорость, касательное и нормальное ускорения точек на ободе маховика в этот момент времени.
Задача 23. Маховик вращается вокруг неподвижной оси; при этом точка, отстоящая от оси вращения на расстоянии r = 0,3 м, движется по закону:
s = 3· t + t 3,
где s – путь движения точки по дуге, м;
t – время, с.
Найти угловую скорость и ускорение маховика в момент t 1 = 3 с.
Задача 24. Маховик диаметром d вращается по закону:
φ = 0,25· t 3 + 4 · t,
где φ – угол поворота, рад;
t – время, с.
Определить среднюю угловую скорость за время между первой и четвертой секундами, угловые скорость и ускорение маховика, а также скорость, касательное и нормальное ускорения точек на ободе маховика в момент t = 3 с.
Задача 25. При запуске электродвигателя ротор радиусом r = 0,4 м вращается по закону:
φ = 0,3· t 3,
где φ – угол поворота, рад;
t - время, с.
Определить угол поворота ротора от начала вращения, его угловые скорость и ускорение, а также линейную скорость, касательное и нормальное ускорения на ободе ротора в момент t1 = 10 с.
Задача 26. Ротор электромотора вращается с частотой 1500 об /мин. После выключения он делает до остановки 250 оборотов. Считая вращение ротора электромотора равнозамедленным, найти время вращения ротора с момента выключения до полной остановки Δ t, а также угловые скорость и ускорение его в период торможения.
Задача 27. Поезд, проходя мимо разъезда, затормозил и далее двигался равнозамедленно. Через 4 мин он остановился на станции, находящейся на расстоянии 2 км от разъезда. Определить скорость v0 в начале торможения и ускорение а.
Задача 28. Шкив диаметром d = 200 мм в течение 10 с вращался с постоянной угловой скоростью ω0 = 4 рад/с. Затем стал вращаться равноускоренно и через 6 с равноускоренного вращения его угловая скорость достигла ω 1 = 10 рад / с.
Определить:
а) число оборотов и среднюю угловую скорость за все время вращения;
б) окружную скорость точек, расположенных на ободе шкива, через 2 с
после начала равноускоренного движения.
Задача 29. Поезд, отходя от станции, движется равноускоренно по закругленному пути радиусом r = 600 м. Определить касательное аt, нормальное аn и полное ускорения поезда через 3 мин, когда пройденный путь равен 1620 м.
Задача 30. Тело движется из состояния покоя и за время t = 15 с его скорость увеличивается до v = 20 м/с. Определить пройденный телом путь и его полное ускорение в конце 15 с, считая движение равноускоренным поступательным по дуге окружности радиуса r = 500 м.
14.2 Контрольные вопросы
а) какое движение твердого тела называется поступательным?
б) что можно сказать о траекториях, скоростях и ускорениях точек тела, совершающего поступательное движение?
в) дайте определение вращательного движения тела вокруг неподвижной оси;
г) что называется угловым перемещением тела?
д) что называется угловой скоростью?
е) какая связь между частотой вращения тела и угловой скоростью вращения?
ж) какое вращательное движение называется равномерным, а какое – равнопеременным?
з) каковы зависимости между угловыми величинами (φ, ω, ε), характеризующими вращательное движение тела, и линейными величинами (S, V, an, at, a), характеризующими движение какой-либо точки этого тела?
и) чему равна угловая скорость минутной стрелки часов?
к) в каких единицах измеряются φ, ω, ε ?
14.3 Литература: [2] c.99 - 107; [3] c.136 - 143; [9] c.79 - 85.
15 САМОСТОЯТЕЛЬНАЯ РАБОТА 9
Тема: Сложное движение точки
Составление кроссворда.
После выполнения самостоятельной работы студент должен:
- иметь представление об относительном, переносном и абсолютном движениях точки;
- знать закон сложного движения точки; разложение сложного движения на относительное и переносное движения; теорему сложения скоростей.
15.1 Задание для самостоятельной работы 9
Составить кроссворд.
15.2 Контрольные вопросы
а) дайте определение сложного движения точки;
б) какое движение называется относительным, переносным, абсолютным?
в) может ли быть равной нулю скорость абсолютного движения точки, если скорости переносного и относительного движения не равны нулю?
г) сформулируйте теорему сложения скоростей при сложном движении точки;
д) по рельсам перемещается башенный кран и поднимает груз. Какое движение является относительным и переносным и как определяется абсолютное движение?
15.3 Литература: [2] c.112 - 114; [3] c.102 - 105; [9] c.86 - 92.
16 САМОСТОЯТЕЛЬНАЯ РАБОТА 10
Тема: Сложное движение твердого тела
Выполнение расчетно-графической работы 5.
После выполнения самостоятельной работы студент должен:
- иметь представление о законе сложного движения, о мгновенной оси вращения и мгновенном центре скоростей;
- знать свойства мгновенного центра скоростей; и способы определения положения мгновенного центра скоростей;
- уметь определять скорость любой точки плоского механизма, определять угловую скорость сложного движения.
16.1 Рекомендуемая последовательность выполнения
расчетно-графической работы 5
а) в соответствии с исходными данными таблицы 27 начертить в масштабе кинематическую схему КШМ (рисунок 89);
б) построить траекторию движения точек А, В, С по следующей последовательности:
1) зная, что точка А кривошипа совершает вращательное движение и ее траектория является окружностью проводим окружность с радиусом ОА и разделим окружность на двенадцать равных частей А1 …А12;
2) из каждой точки А1 , А2, А3 и т.д. циркулем делаем засечки длиной L АВ на оси движения ползуна Х. Найденные точки В1, В2, В3 и т.д. определяют положения ползуна за определенный промежуток времени;
3) учитывая, что шатун совершает плоскопараллельное движение, и точки, лежащие на шатуне АВ совершают траекторию эллипс, построим траекторию точки С. Для этого из точек А1 , А2 ,А3 и т.д. длиной LАС, отметим положения точек С1, С2, С3…..С12. Соединив последовательно полученные точки С1, С2, С3…..С12 плавной кривой, найдем траекторию точки С звена АВ;
в) определить скорость точек А, В, С, используя метод мгновенного центра скоростей для положения 4.
16.2 Задание для самостоятельной работы 10
Построить траектории движения точек А, В и С в соответствии с
рисунком 89. Определить скорости точек А, В, С, используя метод мгновенного центра скоростей. Данные своего варианта взять из таблицы 27, приняв ОА = 20 см.

Рисунок 89 – Схема для выполнения расчетно-графической работы 5
Таблица 27 – Данные для выполнения расчетно-графической работы 5
|
Вариант |
Длина, см |
Угловая скорость, с -1 |
Угол, град |
||
|
АВ |
АС |
w |
a |
b |
|
|
1 |
60 |
20 |
35 |
40 |
45 |
|
2 |
80 |
40 |
40 |
36 |
40 |
|
3 |
100 |
60 |
45 |
60 |
35 |
|
4 |
120 |
50 |
50 |
45 |
30 |
|
5 |
140 |
100 |
60 |
30 |
25 |
|
6 |
160 |
80 |
65 |
36 |
20 |
|
7 |
180 |
90 |
70 |
40 |
15 |
|
8 |
200 |
180 |
75 |
45 |
10 |
|
9 |
180 |
100 |
40 |
45 |
25 |
|
10 |
160 |
100 |
85 |
36 |
0 |
|
11 |
200 |
100 |
90 |
60 |
5 |
|
12 |
140 |
100 |
45 |
60 |
10 |
|
13 |
100 |
60 |
50 |
45 |
45 |
|
14 |
120 |
50 |
50 |
30 |
25 |
|
15 |
160 |
80 |
65 |
40 |
15 |
|
16 |
200 |
100 |
90 |
60 |
10 |
|
17 |
200 |
100 |
15 |
60 |
35 |
|
18 |
180 |
80 |
20 |
45 |
40 |
|
19 |
160 |
60 |
25 |
40 |
45 |
|
20 |
140 |
70 |
30 |
30 |
0 |
|
21 |
120 |
40 |
40 |
40 |
5 |
|
22 |
100 |
50 |
45 |
45 |
10 |
|
23 |
80 |
50 |
50 |
60 |
20 |
|
24 |
60 |
40 |
55 |
45 |
25 |
|
25 |
60 |
20 |
60 |
60 |
30 |
|
26 |
80 |
60 |
65 |
36 |
35 |
|
27 |
100 |
50 |
70 |
40 |
40 |
|
28 |
120 |
60 |
75 |
45 |
45 |
|
29 |
100 |
50 |
45 |
60 |
20 |
|
30 |
60 |
20 |
60 |
40 |
40 |
16.3 Контрольные вопросы
а) какое движение твердого тела называется плоскопараллельным?
б) может ли у какой-либо точки тела, находящегося в плоскопараллель-ном движении, абсолютная скорость равняться нулю?
в) что такое мгновенный центр скоростей?
г) какими способами можно определить положение мгновенного центра скоростей?
д) поезд движется по прямолинейному участку со скоростью V = 80 км /ч. Чему равны минимальная и максимальная скорости точек колеса в его абсолютном движении?
16.4 Литература: [2] c.115 - 119; [3] c.143 - 145; [9] c.86 - 92.
17 САМОСТОЯТЕЛЬНАЯ РАБОТА 11
Тема: Основные понятия и аксиомы динамики
Составление кроссворда.
После выполнения самостоятельной работы студент должен:
- иметь представление о массе тела, об ускорении свободного падения, о двух основных задачах динамики;
- знать основные понятия и аксиомы динамики.
17.1 Задание для самостоятельной работы 11
Составить кроссворд.
17.2 Контрольные вопросы
а) что изучает раздел «Динамика»?
б) что называется массой материальной точки?
в) какова зависимость между силой тяжести тела и его массой?
г) сформулируйте две первые аксиомы динамики, две основные задачи динамики;
д) как формулируются третья и четвертая аксиомы динамики?
е) к двум материальным точкам массой m 1 = 10 кг и m 2 = 20 кг приложены одинаковые силы. Сравните величины ускорений этих точек;
ж) какое свойство тела характеризует его масса?
17.3 Литература: [2] c.123 - 125; [3] c.146 - 147; [9] c.93 - 95.
18 САМОСТОЯТЕЛЬНАЯ РАБОТА 12
Тема: Движение материальной точки. Метод кинетостатики
Изучение вопроса «Понятие о неуравновешенных силах инерции и их влиянии на работу машин».
После выполнения самостоятельной работы студент должен:
- иметь представление о свободной и несвободной материальной точке, об использовании силы инерции при решении технических задач;
- знать формулы для расчета силы инерции при поступательном и вращательном движениях.
18.1 Задание для самостоятельной работы 12
Изучить теоретический материал и составить конспект, раскрывая
следующие понятия:
а) свободная и несвободная материальные точки;
б) понятие о неуравновешенных силах инерции и их влияние на работу машин;
в) балансировка.
18.2 Контрольные вопросы
а) что такое балансировка?
б) объясните неуравновешенность ротора (статическая, моментная, динамическая);
в) что такое дисбаланс (значение, единица измерения)?
г) способы устранения неуравновешенности ротора.
18.3 Литература: [2] c.125 - 129; [3] c.147 - 150; [4] с. 151 - 152;
19 САМОСТОЯТЕЛЬНАЯ РАБОТА 13
Тема: Трение. Работа и мощность
Составление кроссворда.
После выполнения самостоятельной работы студент должен:
- иметь представление о видах трения и силах трения, о коэффициенте трения, о работе силы при прямолинейном и криволинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия;
- знать зависимости для определения силы трения, формулы для расчета работы и мощности при поступательном и вращательном движениях, коэффициента полезного действия.
19.1 Задание для самостоятельной работы 13
Составить кроссворд .
19.2 Контрольные вопросы
а) сформулируйте основной закон трения скольжения;
б) что означает конус трения?
в) всегда ли сила трения является вредной? Укажите случаи, когда сила трения необходима;
г) нужно ли знать величину силы тяжести тела, движущегося по наклонной плоскости при определении коэффициента трения скольжения?
д) какие факторы влияют на величину трения скольжения?
е) вставьте пропущенные слова: работа силы на прямолинейном перемещении равна произведению … на величину перемещения и на косинус угла между направлением силы и направлением…;
ж) чему равна работа силы тяжести при горизонтальном перемещении тела?
з) работа постоянной силы при прямолинейном перемещении W=-10 Дж. Какой угол составляет направление силы с направлением перемещения?
и) вставьте пропущенные слова:
1) работа пары сил равна произведению … на …, выраженный в радианах;
2) мощность при вращательном движении тела равна произведению … на…;
к) как изменится вращающий момент, если при одной и той же мощности уменьшить угловую скорость вращения вала?
19.3 Литература: [2] с.50 - 55, 129 - 137; [3] с.151 - 158; [9].
20 САМОСТОЯТЕЛЬНАЯ РАБОТА 14
Тема: Общие теоремы динамики
Изучение вопроса «Уравнения поступательного и вращательного движений твердого тела».
После выполнения самостоятельной работы студент должен:
- иметь представление о системе материальных точек; внутренних и внешних силах системы, о моменте инерции тела;
- знать основные теоремы динамики, основные уравнения поступательного и вращательного движений твердого тела.
20.1 Задание для самостоятельной работы 14
Изучить теоретический материал и составить конспект, раскрывая следующие понятия:
а) система материальных точек;
б) внешние и внутренние силы системы;
в) основные уравнения поступательного и вращательного движений твердого тела;
г) основные теоремы динамики;
д) момент инерции тела.
20.2 Контрольные вопросы
а) что такое система материальных точек?
б) объясните внешние и внутренние силы системы;
в) запишите уравнение поступательного движения твердого тела;
г) запишите уравнение вращательного движения твердого тела;
д) что характеризует момент инерции тела относительно оси вращения?
е) в чем измеряется момент инерции тела?
ж) сравните формулы динамики для поступательного и вращательного движений твердого тела.
20.3 Литература: [2] с.140 - 149; [3] с.158 - 163; [9] с.121 - 129.
21 САМОСТОЯТЕЛЬНАЯ РАБОТА 15
Тема: Основные положения раздела сопротивления
материалов
Изучение вопроса «Основные гипотезы и допущения, принимаемые в сопротивлении материалов».
После выполнения самостоятельной работы студент должен:
- иметь представление о классификации нагрузок, о внутренних силовых факторах и возникающих при этом деформациях;
- знать основные понятия, гипотезы и допущения сопротивления материалов.
21.1 Задание для самостоятельной работы 15
Изучить теоретический материал и составить конспект, раскрывая следующие понятия:
1) основные гипотезы и допущения, принимаемые в сопротивлении материалов;
2) гипотезы о свойствах деформируемого тела (однородность, изотропность, непрерывность строения);
3) гипотезы о характере деформаций (принцип начальных размеров, линейная зависимость между нагрузками и вызываемыми ими перемещениями, принцип независимости действия сил).
21.2 Контрольные вопросы
а) на каких гипотезах и допущениях основаны выводы расчетных зависимостей в сопротивлении материалов?
б) сформулируйте принцип независимости действия сил в применении к сопротивлению материалов;
в) допустимо ли при малых упругих деформациях бруса, определить момент силы F относительно точки по первоначальному плечу?
21.3 Литература: [2] с.153 - 154; [3] с.55 - 57; [9] с.162 - 167.
22 ПРАКТИЧЕСКАЯ РАБОТА 4
Тема: Растяжение и сжатие
После выполнения практической работы студент должен:
- знать правила построения эпюр продольных сил и нормальных напряжений, закон Р. Гука, зависимости и формулы для расчета напряжений и перемещений, условие прочности и решение трех видов практических задач, порядок расчетов на прочность при растяжении и сжатии;
- уметь строить эпюры продольных сил и нормальных напряжений, составлять расчетные схемы и производить проверочные расчеты прочности элементов механических систем, работающих на растяжение и сжатие, производить проектные расчеты, работать со справочной литературой.
а) вставьте пропущенные слова: « Растяжение или сжатие – это такой вид деформации стержня, при котором в его поперечных сечениях возникает только один внутренний силовой фактор - … сила ».
1) поперечная;
2) продольная.
б) различаются ли внутренние силовые факторы в поперечных сечениях стержней, показанных на рисунках 90, 91?

Рисунок 90 Рисунок 91
1) продольная сила для стержня на рисунке 90 в два раза больше,
чем на рисунке 91;
2) продольные силы на обоих рисунках одинаковы.
в) можно ли считать, что поперечные сечения бруса остаются плоскими и перпендикулярными его оси при деформации?
1) нельзя;
2) можно.
г) как распределяются напряжения по поперечным сечениям бруса при осевом растяжении и сжатии?
1) в любом поперечном сечении по длине бруса напряжения распределены равномерно;
2) в сечениях, удаленных от места приложения нагрузки на расстояние больше ширины поперечного сечения, напряжения распределены равномерно;
3) в сечениях, достаточно удаленных от точки приложения нагрузки (при условии отсутствия резкого изменения формы бруса), напряжения распределены равномерно.
д) зависят ли напряжения, возникающие при растяжении (сжатии) призматических стержней, от формы их поперечного сечения (квадрат, прямоугольник, двутавр и т. д.)?
1) зависят;
2) не зависят.
е) зависит ли величина напряжений, возникающего в поперечном сечении стержня, от материала, из которого изготовлен стержень?
1) зависит;
2) не зависит.
ж) образцы из стали и дерева с равной площадью поперечного сечения растягиваются одинаковыми силами. Будут ли равны возникающие в образцах напряжения?
1) в стальном образце возникнут большие напряжения, чем деревянном;
2) в образцах возникнут равные напряжения.
з) вычислите величину продольной силы, возникающей в поперечном сечении растянутого стержня, если нормальное напряжения в этом сечении равны 140 Н / мм 2, а его площадь составляет 100 мм 2.
1) ![]() кН;
кН;
2) ![]() кН.
кН.
и) вставьте пропущенное слово «Условие прочности состоит в том, что рабочие напряжения не должны превышать ……. напряжения »;
1) допускаемого;
2) расчетного.
к) рабочее напряжение, возникающее в детали, равно s = 160 Н / мм 2, опасное (предельное) напряжение для материала детали sпред = 320 Н / мм2. Определить коэффициент запаса прочности.
1) 2; 2) 0,5.
л) допускаемое
напряжение при расчете на прочность было принято ![]() 180 Н / мм2. После
окончательного выбора размеров конструкции рабочее напряжение оказалось равным s = 185 Н / мм 2. Грозит ли
конструкции опасность разрушения ? Показать расчет перегрузки (недогрузки)
конструкции.
180 Н / мм2. После
окончательного выбора размеров конструкции рабочее напряжение оказалось равным s = 185 Н / мм 2. Грозит ли
конструкции опасность разрушения ? Показать расчет перегрузки (недогрузки)
конструкции.
1) конструкция может разрушиться;
2) конструкции не грозит опасность разрушения.
м) как изменится вес конструкции, если при подборе ее сечения уменьшить нормативных коэффициент запаса прочности?
1) вес конструкции уменьшится;
2) вес конструкции не изменится.
н) как повлияет уменьшение нормативного коэффициента запаса прочности, принятого при расчете конструкции, на ее прочность?
1) прочность конструкции уменьшится;
2) прочность конструкции увеличится.
22.2 Расчетные формулы
Нормальное напряжение σ, Па
![]() ,
,
где ![]() - продольная сила, Н;
- продольная сила, Н;
А – площадь поперечного сечения, м 2 .
Удлинение (укорочение) бруса ![]() ,
м
,
м
![]() =
= ![]() ,
,
где ![]() – абсолютное удлинение
(укорочение) бруса, м ;
– абсолютное удлинение
(укорочение) бруса, м ;
![]() - начальная длина бруса, м;
- начальная длина бруса, м;
E – модуль продольной упругости, Па.
![]() – жесткость сечения,
которая характеризует физико-механические свойства материала и геометрические размеры сечения.
– жесткость сечения,
которая характеризует физико-механические свойства материала и геометрические размеры сечения.
Допускаемое
напряжение ![]() , Па
, Па
![]() ,
,
где ![]() - предельное (опасное) напряжение,
Па;
- предельное (опасное) напряжение,
Па;
![]() - требуемый (нормативный)
коэффициент запаса.
- требуемый (нормативный)
коэффициент запаса.
Условие прочности при растяжении и сжатии
![]() £
[s]
£
[s]
Исходя из условия прочности, производят три вида расчетов:
- проверочный расчет (проверка прочности)
![]() £
[s]
£
[s]
- проектный расчет (подбор сечений)
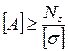
- определение допускаемой нагрузки
[Νz] £ А [s ]
22.3 Последовательность проверочного расчета
1 Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы и места изменения размеров поперечного сечения.
2 Определить по методу сечений продольную силу для каждого участка (ординаты эпюры Nz), построить эпюру продольных сил Nz. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получанные значения ординат.
Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
3 Для построения эпюры нормальных напряжений определить напряже -ния в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображать прямой, параллельной оси бруса.
4 Перемещение свободного конца бруса определить как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
5 Произвести проверку прочности.
22.4 Пример 1. Проверочный расчет
Для данного стального ступенчатого бруса в
соответствии с рисунком 92 построить эпюру продольных сил ![]() и нормальных
напряжений
и нормальных
напряжений ![]() ; определить
перемещение свободного конца ∆ℓ;
произвести проверочный расчет, если [s] =160 МПа.
; определить
перемещение свободного конца ∆ℓ;
произвести проверочный расчет, если [s] =160 МПа.
F1 = 30 кН; F2 = 38 кН; F3 = 42 кН; А1 = 1,9 см 2; А2 =3,1 см 2
Решение
1 Разбиваем брус на участки 1, 2, 3, 4, 5.
2 Применяя метод сечений, определяем значения продольных сил Nz, Н, на участках бруса
![]()
Рисунок 92
![]() ;
; ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Строим эпюру продольных сил N z в соответствии с рисунком 92.
3
Вычисляем значения нормальных напряжений ![]() , МПа, по
формулам:
, МПа, по
формулам:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Строим эпюру нормальных напряжений в соответствии с рисунком 92.
4 Определяем перемещение свободного конца ![]() , мм, по формуле
, мм, по формуле
![]() =
= ![]() 1 +
1 + ![]() 2 +
2 +![]() 3 +
3 + ![]() 4 +
4 + ![]() 5
5
![]() 1
=
1
= 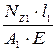 ;
;
![]() 1 = 0;
1 = 0;
![]() 2 =
2 = ![]() ;
;
![]() 2 =
2 = ![]() ;
;
![]() 3
=
3
= ![]() ;
; ![]() 3 =
3 = ![]() ;
;
![]() 4 =
4 = 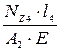 ;
; ![]() 4 =
4 = ![]() ;
;
![]() 5 =
5 = 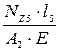 ;
; ![]() 5 =
5 = ![]() ;
;
![]() = 0 + 0,394 + 0,0484 –
0,0516 – 0,161 = 0,23 мм.
= 0 + 0,394 + 0,0484 –
0,0516 – 0,161 = 0,23 мм.
5 Проверяем условия прочности
![]() £
[s]
£
[s]
Так как ![]() = 161,3 МПа, больше допустимого
напряжения [s] вычисляем перегрузку
= 161,3 МПа, больше допустимого
напряжения [s] вычисляем перегрузку ![]()
![]() =
= ![]() ;
;
![]() =
=
![]() , что меньше допускаемого значения
перегрузки равного 5
, что меньше допускаемого значения
перегрузки равного 5 ![]() .
.
Условия прочности выполняется, брус удлинился на 0,23мм.
22.5 Последовательность проектного расчета
1 Определить реакции стержней, используя уравнения равновесия для плоской системы сходящихся сил, и проверить правильность найденных реакций.
2 Для наиболее нагруженного стержня, используя условие прочности 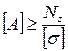 , определить требуемую
площадь поперечного сечения стержня и
подобрать по сортаменту подходящий номер профиля и найти стандартное значение
площади поперечного сечения стержня.
, определить требуемую
площадь поперечного сечения стержня и
подобрать по сортаменту подходящий номер профиля и найти стандартное значение
площади поперечного сечения стержня.
3 Определить процент пере- или недогрузки наиболее нагруженного стержня.
22.6 Пример 2. Проектный расчет
Для данной системы двух стержней одинакового поперечного сечения, нагруженных силой F = 170 кН (рисунок 93), определить:
а) требуемую площадь поперечных сечений стержней, состоящих из двух равнобоких уголков, и подобрать по ГОСТу соответствующий профиль уголка;
б) процент пере – или недогрузки наиболее нагруженного стержня при принятых стандартных размерах сечения, приняв [s] = 130 МПа.
Решение
1 В данном примере в шарнире С приложена система сходящихся сил. Определяем силы N1 и N2 в стержнях 1 и 2 (рисунок 93), используя уравнения равновесия.
![]() ;
;
![]() ;
;

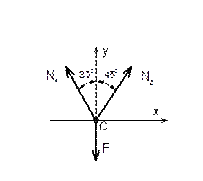
Решение 93
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Проверяем правильность определения сил N1 и N2 построением силового многоугольника (рисунок 94).
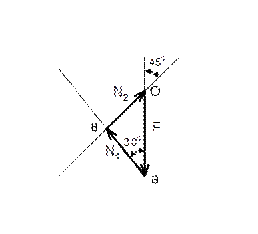
Рисунок 94
2 Определяем требуемую площадь поперечного сечения для наиболее нагруженного стержня: N max = N1 = 124,2 кН
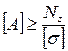 ;
;
![]() ;
;
Площадь равнобокого уголка подбираем по условию ![]() :
:
А1/2 = 9,56 / 2 = 4,78 см2.
Назначаем профиль № 6,3 ( 63 х 63 х 4 ) ГОСТ 8509 - 72, площадью
[A] = 4,96 см2. Таким образом, требуемая площадь поперечного сечения стержней будет равна:
![]() см2.
см2.
Рабочее напряжение в поперечном сечении наиболее нагруженного стержня:
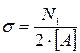 ;
;
![]() .
.
3 Проверяем прочность наиболее нагруженного стержня
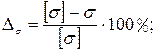
![]() .
.
Недогрузка составляет 3,69 %, что меньше допустимого значения - 10%.
22.7 Задание для бригад
Для заданного стального ступенчатого бруса (рисунок 95) требуется:
а) построить эпюру продольных сил ![]() и нормальных
напряжений
и нормальных
напряжений ![]() по длине бруса;
по длине бруса;
б) определить удлинение (укорочение) бруса ![]() ;
;
в) проверить условие прочности, если [s] = 160 МПа.
P 1 = 15 кН; Р 2 = 10 кН; Р 3 = 5 кН; А 1 = 1,2 см2; А 2 = 2,0 см2, а = 0,2 м,
в = 0,4 м, с = 0,5 м.
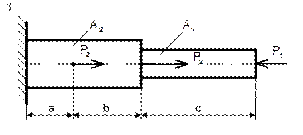
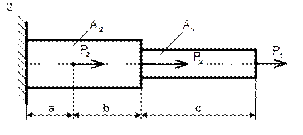
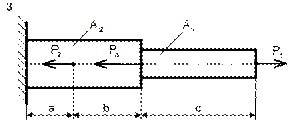
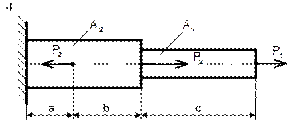
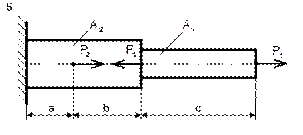
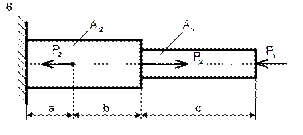
Рисунок 95
22.8 Литература: [2] с.159 - 166, [3] с. 170 - 173; [9] с.176 -182.
23 ЛАБОРАТОРНАЯ РАБОТА 2
Тема: Определение модуля продольной упругости
После выполнения лабораторной работы студент должен:
- иметь представление о механических свойствах и характеристиках материалов; допускаемых нагрузках на работающие детали;
- знать закон Гука, механические свойства и характеристики материалов; допускаемые нагрузки на работающие детали;
- уметь определить физические и механические свойства стального образца; работать со справочной литературой.
23.1 Теоретическое обоснование
Изменение длины стержня ∆l, мм, для большинства материалов определяют по формуле:
![]() ,
,
где NZ – продольная сила. Н;
l – расчетная длина стержня, м, для которой определяется удлинение;
E – модуль продольной упругости, Па;
А – площадь поперечного сечения, м 2.
Измерив опытным путем величину осевой нагрузки ∆Р и изменение длины ∆l (зная размеры A и l испытуемого стержня), вычисляют модуль продольной упругости:
![]() ,
,
где N z
= ![]() - осевая нагрузка, Н.
- осевая нагрузка, Н.
Чтобы установить зависимость удлинения ∆l от осевой нагрузки ![]() , нагружение образца
производят несколькими ступенями, при этом нагрузка каждый раз увеличивают на одну и ту же величину. После каждого нагружения измеряют удлинение ∆l. Приращение удлинения на одну и ту же величину подтверждает наличие
прямой пропорциональности между деформацией и нагрузкой, т.е. справедливость
закон Гука.
, нагружение образца
производят несколькими ступенями, при этом нагрузка каждый раз увеличивают на одну и ту же величину. После каждого нагружения измеряют удлинение ∆l. Приращение удлинения на одну и ту же величину подтверждает наличие
прямой пропорциональности между деформацией и нагрузкой, т.е. справедливость
закон Гука.
Величина ступени нагружения ∆Р зависит от материала
образца и размеров его поперечного сечения; ее выбирают таким образом, чтобы
наибольшая нагрузка при испытании не вызывала остаточной
деформации. Наибольшую нагрузку для материала образца
можно определить по величине предела пропорциональности ![]() . Если он неизвестен, то
его можно приближенно найти по пределу текучести
. Если он неизвестен, то
его можно приближенно найти по пределу текучести ![]() :
:
![]()
![]()
Таким образом, наибольшая нагрузка
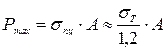 .
.
При числе ступней нагружения n величина каждой ступени нагружения
∆Р = Р max / n.
23.2 Машина для испытания
Для работы используется универсальная машина типа Р – 5, пригодная для испытания на растяжение.
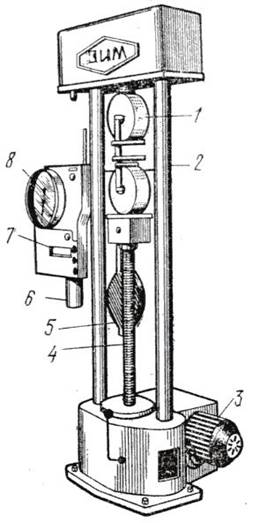
1,2 – универсальные захваты;
3 – электродвигатель;
4 – винт;
5 – направляющие колонны;
6 – рычажная система с маятником;
7 - пишущее устройство;
8 - круговая шкала нагрузок.
Рисунок 96
Универсальная машина Р – 5 предназначенная для статических испытаний на растяжение, сжатие и изгиб (при наличии специального приспособления на этой машине можно проводить испытания на срез), снабжена универсаль -ными захватами 1 и 2 (рисунок 96). При установке образца для испытания на растяжение нижний захват 2 перемещается вручную вдоль направляющих колонн 5 рукояткой. После закрепления образца в захватах машины включают электродвигатель 3, который через коробку скоростей вращает гайку, при этом винт 4 перемещает нижней захват 2 вниз.
Закрепленный в машине образец соединяет верхний и нижний захваты, поэтому перемещение нижнего захвата повлечет за собой перемещение верхнего захвата. Последний связан через рычажную систему с маятником 6, который будет отклоняться от вертикального положения. Сила, растягивающая образец, определяется углом отклонения маятника от вертикального положения. Отклонение маятника передается на механизм, перемещающий стрелку круговой шкалы нагрузок 8.
Для вычерчивания диаграммы испытательная машина снабжена пишущим устройством (перо или карандаш) и барабаном, на который наматывается перфорированная миллиметровая бумага 7.
Модуль упругости определяют при упругих деформациях, величина которых незначительна. Для их измерения применяют тензометры, которые устанавливают непосредственно на образце (тем самым исключается влияние деформаций элементов самой испытательной машины).
Для определения линейных перемещений применяем рычажный тензометр.
Рычажный тензометр (схема
тензометра показана на рисунке 97)
применяют для измерения малых линейных перемещений. Тензометр прижимают к
испытуемому образцу 1 при помощи струбцинки двумя ножами 8 и 2. Расстояние ![]() между ножами является базой
тензометра (обычно 20 мм, но с помощью специальных удлинителей база может быть
увеличена до 50 или 100 мм). При деформации образца расстояние между ножами
изменяется.
между ножами является базой
тензометра (обычно 20 мм, но с помощью специальных удлинителей база может быть
увеличена до 50 или 100 мм). При деформации образца расстояние между ножами
изменяется.
Подвижный нож 8 повернется и отклонит рычаг 7. Отклонение рычага 7 через тягу 6 передается на стрелку 4, которая повернется вокруг оси, закрепленной на рамке 5.
Перемещение стрелки по шкале 3 пропорционально изменению расстояния между ножами, но значительно больше в зависимости от соотношения плеч рычагов 7 и 4.
а) б)
Рисунок 97 – Рычажный тензометр
Шкала тензометра проградуирована в миллиметрах. Отношение отсчета по шкале к изменению расстояния между ножами называют коэффициентом увеличения тензометра.
![]() =
= ![]() ,
,
где b, a, h, H - размеры плеч рычагов, отмеченных на рисунке 97, б.
Коэффициент увеличения рычажных тензометров 1000 - 1200. Его значение для каждого тензометра указывается в его паспорте.
В зависимости от того, будет ли при деформации образца расстояние ме-жду ножами увеличиваться или уменьшаться, перед началом испытаний уста -навливают стрелку тензометра в начале или в конце шкалы. Для определения деформации образца следует отметить первоначальное положение стрелки А0, затем после нагружения отметить положение отклонившейся стрелки А1. Величина удлинения равна разности отсчетов А1 - А0, разделенной на коэффициент увеличения тензометров:
![]() .
.
Пример. Коэффициент увеличения тензометра
![]()
![]() 1000, отсчет по шкале до нагружения образца А0
= 3,5мм, после нагружения образца А1= 6,5
мм. Величина удлинения
1000, отсчет по шкале до нагружения образца А0
= 3,5мм, после нагружения образца А1= 6,5
мм. Величина удлинения
![]() ;
; ![]() .
.
23.3 Форма и размер образцов
Модуль продольной упругости определяем при испытании на растяжение. При испытании на образце устанавливаем прибор измеряющей деформацию, поэтому длина образца должна быть сравнительно большой.
Форма поперечного сечения образца зависит от конструкции прибора для измерения деформации. Применяем образцы круглого поперечного сечения.
23.4 Порядок выполнения работы
1 Ознакомиться с устройством испытательной машины и принципом действия тензометров, в отчет записать цену деления шкалы силоизмеритель-ного устройства, коэффициент увеличения тензометров, базу тензометра и размеры поперечного сечения образца.
2 Определить величину ступени нагружения.
3 Произвести предварительное нагружение для обжатия головок образца в захватах машины, нагрузка Р1 при этом может быть равна или несколько больше ступени нагружения. Зафиксировать величину нагрузки и произвести первый отсчет по шкалам тензометра.
4 Провести 4 - 5 нагружений образца равными ступенями и после каждого нагружения в таблицу 28 записать показания левого и правого тензометров. Закончив испытания, образец разгрузить.
5 Обработать результаты испытания. Вычислить приращение ![]() ср зарегистрированное
тензометрами. Для этого находят сумму отсчетов по левому и правому тензометрами
А + Б, а затем вычитают предыдущее показание тензометра из последующего.
Приращение
ср зарегистрированное
тензометрами. Для этого находят сумму отсчетов по левому и правому тензометрами
А + Б, а затем вычитают предыдущее показание тензометра из последующего.
Приращение ![]() ср определяют как среднее
значение всех произведенных изменений.Так как нагружение производилось равными
ступенями, то удлинение должно возрастать на одну и ту же величину, что
подтвердит справедливость закона Гука.
ср определяют как среднее
значение всех произведенных изменений.Так как нагружение производилось равными
ступенями, то удлинение должно возрастать на одну и ту же величину, что
подтвердит справедливость закона Гука.
6 Вычислить модуль продольной упругости Е.
23.5 Отчет о работе
Тема: Определение модуля продольной упругости.
Цель работы: Проверка закона Гука и определение величины модуля продольной упругости Е.
Оборудование и принадлежности: Испытательная машина, штангенциркуль, стальной образец, тензометры. чертежные принадлежности, вычислительная машинка.
Ход работы
1. Записать тип и наименование испытательной
машины, цену деления шкалы, тип и наименование тензометра; базу тензометра ![]() =…мм, вычислить коэффициент увеличения тензометра
=…мм, вычислить коэффициент увеличения тензометра ![]() =…
=…
2. Записать и вычислить данные об образце:
а) материал образца;
б) диаметр образца d, мм;
в) площадь поперечного сечения A, мм 2;
г) предел пропорциональности ![]() ,
Н/ мм 2;
,
Н/ мм 2;
д) наибольшая нагрузка ![]() ,
Н
,
Н
![]() ;
;
е) число ступней нагружения n ;
ж) величина ступени нагружения ∆Р, Н.
3. Оформить таблицу записи результатов испытания.
Таблица 28 - Результаты испытания
|
|
Нагрузка, Н |
Отсчеты по шкалам тензометров |
Сумма отсчетов А + Б |
Приращение отсчетов Δ (А + Б) |
||
|
Р |
Δ Р |
левая А |
правая Б |
|||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
4. Вычислить модуль продольной упругости:
а) среднее приращение нагрузки, Δ Р ср , кгс;
б) среднее приращение отсчетов Δ (А + Б) ср, мм;
в) изменение
длины образца ![]() (база
тензометра) от нагрузки Δ Р ср , мм;
(база
тензометра) от нагрузки Δ Р ср , мм;
Δ
![]() ср
=
ср
=![]() ;
;
г) модуль продольной упругости, кгс / см 2 , Н / мм 2
![]() ;
;
5 Выполнить диаграмму процесса деформации;
6 Ответить на контрольные вопросы.
23.6 Контрольные вопросы
а) какое свойство материала характеризует модуль продольной упругости;
б) что нужно измерить опытным путем при определении модуля продольной упругости;
в) почему при определении модуля продольной упругости напряжения не должны превышать предела пропорциональности;
г) как вычисляется наибольшая нагрузка, которую не следует превышать при испытании;
д) почему модуль продольной упругости удобнее определить при растяжении, а не при сжатии;
е) какую закономерность можно установить, если регистрировать показания тензометров, увеличивая нагрузку равными ступенями.
2.3.7 Литература: [2] с.159 - 166, [3] с. 170 - 173; [9] с.176 -182;
[6] с.74 -81.
24 САМОСТОЯТЕЛЬНАЯ РАБОТА 16
Тема: Растяжение и сжатие
Выполнение расчетно-графической работы 6
После выполнения самостоятельной работы студент должен:
- иметь представление о продольных силах, о нормальных напряжениях в поперечных сечениях, о продольных и поперечных деформациях и их связи, о предельных и допускаемых напряжениях, о коэффициенте запаса прочности;
- знать правила построения эпюр продольных сил и нормальных напряжений, закон Гука, зависимости и формулы для расчета напряжений и перемещений, условие прочности;
- уметь строить эпюры продольных сил и нормальных напряжений, работать со справочной литературой.
24.1 Рекомендуемая последовательность для выполнения
расчетно-графической работы 6
а) разбить брус на участки;
б) определить ординаты эпюры продольных сил на участках бруса;
в) вычислить ординаты эпюры нормальных напряжений;
г) построить эпюры продольных сил и нормальных напряжений;
д) определить перемещение свободного конца бруса.
24.2 Задание для самостоятельной работы 16
Двухступенчатый стальной брус в соответствии с рисунком 98 нагружен силами F1, F2, F3. Построить эпюры продольных сил N z и нормальных напряжений σ по длине бруса. Определить перемещение свободного конца бруса, приняв Е = 2∙105 МПа.
Числовые значения F1, F2, F3 , а также площади поперечных сечений ступеней А1 и А2 для своего варианта взять из таблицы 29.
Таблица 29 – Данные для выполнения расчетно-графической работы 6
|
Схема в соответствии с рисунком 98 |
Вариант |
Сила, кН |
Площадь поперечного сечения, см2 |
|||
|
F1 |
F2 |
F3 |
А1 |
А2 |
||
|
1 |
01 11 21 |
30 16 17 |
10 15 13 |
5 10 8 |
1,8 1,1 1,0 |
3,2 1,8 2,2 |
|
2 |
30 10 20 |
11 12 18 |
6 5 10 |
2 3 5 |
1,1 1,0 1,9 |
1,6 1,5 2,7 |
|
3 |
02 12 23 |
16 8 15 |
25 13 24 |
28 14,5 29 |
1,2 0,6 1,3 |
3,8 2,1 3,9 |
|
Продолжение таблицы 29 |
||||||
|
Схема в соответствии с рисунком 98 |
Вариант |
Сила, кН |
Площадь поперечного сечения, см2 |
|||
|
F1 |
F2 |
F3 |
А1 |
А2 |
||
|
4 |
03 13 22 |
26 14 24 |
9 5 10 |
3 1,5 3,5 |
1,9 1,0 2,0 |
1,6 0,7 1,7 |
|
5 |
05 15 25 |
14 17 20 |
16 19 18 |
10 13 12 |
2,1 2,4 2,5 |
1,9 2,1 2,2 |
|
6 |
04 14 24 |
28 19 26 |
22 14 20 |
12 4 10 |
4,8 2,9 4,6 |
2,6 1,8 2,4 |
|
7 |
07 17 27 |
17 20 14 |
13 17 10 |
8 10 6 |
2 2,2 1,7 |
2,5 2,7 2,3 |
|
8 |
06 16 26 |
10 17 9 |
12 19 11 |
13 20 12 |
0,9 1,6 1,0 |
0,7 1,4 0,8 |
|
9 |
09 19 29 |
40 31 25 |
55 46 41 |
24 20 18 |
2,8 1,9 1,6 |
3,4 2,5 2,1 |
|
10 |
08 18 28 |
29 15 30 |
2 1,1 4 |
54 34 56 |
1,9 0,8 2,0 |
1,4 0,5 1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 98
24.3 Контрольные вопросы:
а) как нагрузить прямой стержень, чтобы он испытывал только растяжение?
б) что такое продольная и поперечная деформации бруса при растяжении (сжатии)? Какова зависимость между ними?
в) сформулируйте закон Гука;
г) каков физический смысл модуля продольной упругости Е?
д) что называется эпюрой продольных сил бруса?
е) как определить нормальное напряжение в поперечном сечении бруса?
ж) какие поперечные сечения бруса называют опасными?
з) какая величина в формуле Гука характеризует жесткость материала?
и) как определяют удлинение (укорочение) участка бруса с постоянным поперечным сечением и постоянной продольной силой по всей его длине?
к) зависит ли нормальное напряжение от формы поперечного сечения?
л) во сколько раз изменится удлинение бруса, если при прочих равных условиях:
1) увеличить длину бруса в 2 раза;
2) увеличить диаметр бруса в 2 раза. Как отразятся подобные изменения на прочности бруса?
24.4 Литература: [2] с.159 - 166, [3] с. 170 - 173; [9] с.176 -182.
25 САМОСТОЯТЕЛЬНАЯ РАБОТА 17
Тема: Практические расчеты на срез и смятие:
Изучение вопроса «Расчет сварных и заклепочных соединений».
После выполнения самостоятельной работы студент должен:
- иметь представление о деталях, работающих на срез и смятие;
- знать внутренние силовые факторы, напряжения и деформации, условия прочности при сдвиге и смятии.
25.1 Задание для самостоятельной работы 17
Изучить теоретический материал и составить конспект, раскрывая следующие понятия:
а) основные расчетные предпосылки и условности расчетов;
б) условия прочности;
в) допускаемые напряжения;
г) формулы для расчета сварных и заклепочных соединений;
д) примеры расчетов сварных и заклепочных соединений.
25.2 Контрольные вопросы
а) на каких допущениях основаны расчеты на срез?
б) какова зависимость между допускаемыми напряжениями растяжения, среза и смятия?
в) по каким формулам производят расчет на срез и смятие? сформулируйте условие прочности;
г) что такое смятие? На каких допущениях основаны расчеты на смятие?
д) как определяется площадь смятия, если поверхность смятия цилиндрическая и поверхность смятия плоская?
е) чем отличается расчет на прочность при сдвиге односрезной заклепки от двухсрезной?
ж) диаметр заклепки увеличился в 2 раза. Как изменится расчетное напряжение среза?
1) уменьшится в 2 раза;
2) уменьшится в 4 раза;
з) во сколько раз изменится допускаемая нагрузка на сварное соединение, если толщина шва уменьшится вдвое (при прочих равных условиях)?
1) уменьшится в 4 раза;
2) уменьшится в 2 раза.
25.3 Литература: [2] с.177 - 180; [3] с.76 - 80; [9] с.197 - 207.
26 САМОСТОЯТЕЛЬНАЯ РАБОТА 18
Тема: Геометрические характеристики плоских сечений
Изучение вопроса «Определение главных центральных моментов инерции составных сечений, имеющих ось симметрии».
После выполнения самостоятельной работы студент должен:
- иметь представление о физическом смысле и порядке определения осевых, центробежного и полярного моментов инерции, о главных центральных осях и главных центральных моментах инерции;
- знать формулы моментов инерции простейших сечений.
26.1 Задание для самостоятельной работы 18
Изучить теоретический материал и составить конспект. раскрывая следующие понятия:
а) статический момент сечения;
б) осевые, центробежный и полярный моменты инерции;
в) связь между осевыми и полярным моментами инерции;
г) главные оси и главные центральные моменты инерции простейших сечений (прямоугольника, круга, кольца).
26.2 Контрольные вопросы
а) что такое статический момент сечения?
б) как определяют статический момент сечения относительно произвольной оси?
в) чему равен статический момент сечения относительно центральной оси?
г) что такое центробежный момент инерции?
д) что такое осевой момент инерции сечения?
е) какова единица измерения осевого момента инерции?
ж) какова зависимость между осевыми и полярным моментами инерции данного сечения?
з) что такое полярный момент инерции сечения бруса?
26.3 Литература: [2] с.192 - 201; [3] с.48 - 53; [9] с.208 - 215.
27 ПРАКТИЧЕСКАЯ РАБОТА 5
Тема: Кручение
После выполнения практической работы студент должен:
- знать внутренние силовые факторы при кручении; распределение напряжений по сечению; закон Гука при сдвиге; условия прочности и жесткости при кручении и решение трех видов задач;
- уметь строить эпюры крутящих моментов; выполнять проектный и проверочный расчеты круглого бруса для статически определимых систем; составлять расчетные схемы и производить проверочные расчеты прочности валов; производить проектные расчеты валов, работающих на кручение.
27.1 Тестовый контроль
а) применима ли гипотеза плоских сечений при кручении брусьев круглых сплошных и кольцевых сечений?
1) не применима;
2) применима.
б) изменяются ли расстояния между поперечными сечениями скручиваемого бруса?
1) не изменяются;
2) изменяются.
в) искривляются ли радиусы поперечных сечений при кручении бруса цилиндрической формы?
1) искривляются;
2) не искривляются.
г) справедлив ли закон Гука при кручении, если напряжение не превышает предела пропорциональности материала при кручении.
1) справедлив;
2) не справедлив.
д) укажите, для какой точки поперечного сечения (рисунок 99) можно вычислить напряжение по формуле:
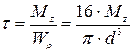

Рисунок 99
1) для точки А;
2) для точки В;
3) для точки О.
е) во сколько раз напряжение в точке А (рисунок 99) меньше напряжения в точке В.
1) в четыре раза;
2) в два раза.
ж) указать на рисунке 100 правильную эпюру М z, если:
М 1 = 6 Н ×м; М 2 = 2 Н ×м; М 3 = 4 Н ×м.
Рисунок 100
1) рисунок 100,1;
2) рисунок 100,2;
3) рисунок 100,3.
з) указать на рисунке 101 правильную эпюру М z, если:
М 1 = 5 Н ×м; М 2 = 6 Н ×м; М 3 = 11 Н ×м.
1) рисунок 101,1;
2) рисунок 101,2;
3) рисунок 101,3.
Рисунок 101
к) зависит ли величина рабочих (расчетных) касательных напряжений от материала вала?
1) зависит;
2) не зависит.
л) зависит ли угол поворота сечения вала от материала, из которого он изготовлен?
1) зависит;
2) не зависит.
м) как изменится величина максимального напряжения вала в поперечных сечениях, если диаметр вала увеличить в два раза?
1) уменьшится в два раза;
2) уменьшится в четыре раза;
3) уменьшится в восемь раз.
27.2 Расчетные формулы
Условие прочности при кручении
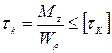 ,
,
где t к - расчетное касательное напряжение, Н/м 2;
Мz - наибольший крутящий момент, Нм;
Wr - момент сопротивления при кручении, м 3 ;
[t к ] - допускаемое касательное напряжение при кручении, Н / м 2.
Проектный расчет из условия прочности
Сечение вала - круг: 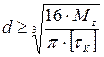 ;
;
Сечение вала - кольцо: 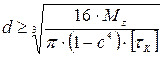 ,
,
где d – наружный диаметр круглого сечения, м;
c – коэффициент;
c = d вн / d,
где d вн – внутренний диаметр кольцевого сечения, м.
Условие жесткости при кручении
![]() ,
,
где φ0 - относительный угол закручивания сечения, рад / м;
G - модуль сдвига, Н /м 2;
![]() r - полярный момент
инерции сечения, м 4;
r - полярный момент
инерции сечения, м 4;
[φ0] - допускаемый угол закручивания сечения
[φ0] = ![]() .
.
Проектный расчет из условия жесткости
![]()
Сечение вала - круг: ![]() ;
; 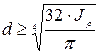 ;
;
Сечение вала - кольцо: ![]() ;
; 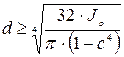
27.3 Последовательность решения задачи
1 Определить внешний скручивающий момент М, Н×м, по формуле
М = ![]() ,
,
где Р – мощность, Вт;
w- угловая скорость, с -1.
2 Определить уравновешивающий момент, используя уравнение равновесия Σ М кz = 0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.
3 Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.
4 Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала круглого или кольцевого сечения:
а) из условия прочности
Сечение вала - круг: 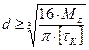 ;
;
Сечение вала - кольцо: 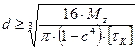 ,
,
б) из условия жесткости
Сечение вала - круг: ![]() ;
;
Сечение вала - кольцо: 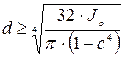
Из двух полученных диаметров вала выбрать наибольший.
27.4 Пример 1. Проектный расчет из условий прочности и
жесткости
Для стального вала круглого поперечного сечения постоянного по длине, показанного на рисунке 102, требуется:
1) определить значения моментов М 2, М 3, соответствующие передаваемым мощностям Р 2 , Р 3, а также уравновешивающий момент М 1;
2) построить эпюру крутящих моментов;
3) определить требуемый диаметр вала из расчетов на прочность и жест -кость, если: [tк] = 30 МПа; [φ 0] = 0,02 рад/м; w = 20 с -1; Р 2 =52 кВт; Р 3 =50 кВт; G = 8 × 104 МПа.
Окончательное значение диаметра округлить до ближайшего четного (или оканчивающего на пять) числа.
Решение
1 Определяем величины скручивающих моментов М 2 и М 3
![]()
![]() ;
;
![]()
![]() .
.
2 Определяем уравновешивающий момент М 1
SМz = 0; - М 1 + М 2 + М 3 =0;
М 1 = М 2 + М 3; М 1 = 2600 + 2500 = 5100 Н ×м;
3 Строим эпюру М z в соответствии с рисунком 102.
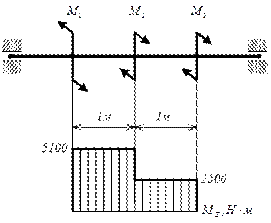
Рисунок 102
4 Определяем диаметр вала для опасного участка, из условий прочности и жесткости (М z maх = 5100 Н ×м).
Из условия прочности
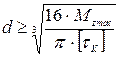
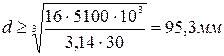 .
.
Из условия жесткости
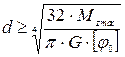
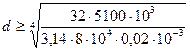 = 75,5
мм
= 75,5
мм
Требуемый диаметр вала получился больше из расчета на прочность, поэтому его принимаем как окончательный: d = 96 мм.
27.5 Задание для бригад
Для стального вала постоянного поперечного сечения требуется определить значения моментов М 1, М 2 и М 3, а также уравновешивающий момент М 0; построить эпюры крутящих моментов; определить требуемый диаметр вала из расчетов на прочность и жесткость , если [tк] = 20 МПа;
[φ0]= 0,02 рад / м; w = 30 с -1; G = 8 × 10 4 МПа.
Данные взять из таблицы 30 и в соответствии с рисунком 103.
Окончательное значение диаметра округлить до ближайшего четного (или оканчивающего на пять) числа.
Таблица 30 - Исходные данные
|
Мощность, кВт |
Вариант |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Р 1 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
3,0 |
|
Р 2 |
2,6 |
2,7 |
2,8 |
2,9 |
3,0 |
3,1 |
3,2 |
3,3 |
3,4 |
3,5 |
|
Р 3 |
3,1 |
3,2 |
3,3 |
3,4 |
3,5 |
3,6 |
3,7 |
3,8 |
3,9 |
4,0 |
![]()
Рисунок 103
27.6 Литература: [2] с.153 - 154; [3] с.55 - 57; [9] с.162 - 167.
28 ЛАБОРАТОРНАЯ РАБОТА 3
Тема: Испытание на кручение стального образца
После выполнения лабораторной работы студент должен:
- знать распределение касательных напряжений по сечению, характер разрушения различных материалов;
- уметь определить физические и механические свойства стального образца на испытательной машине.
28.1 Теоретическое обоснование
При кручении бруса круглого поперечного сечения в плоскостях, перпендикулярных его продольной оси, и в плоскостях, совпадающих с этой осью, возникают только касательные напряжения; в плоскостях, расположенных под углом 450 к оси бруса, - только нормальные напряжения (главные). Нормальные и касательные напряжения равны между собой, поэтому разрушение образца при кручении может произойти от сдвига или от отрыва. Так как сопротивление сдвигу и отрыву у различных материалов неодинаково, разрушение образцов при испытании на кручении происходит различно.
На рисунке 104 показано разрушение стального образца, вызванное сдвигом по его поперечному сечению

Рисунок 104
На рисунке 105 показано разрушение чугунного образца, от отрыва по винтовой поверхности с углом наклона 450 к его оси.

Рисунок 105
На рисунке 106 показано разрушение деревянного образца, вызванное сдвигом в продольных осевых сечениях

Рисунок 106
28.2 Машина для испытания
Для испытания на кручение применяют специальные машины типа КМ - 50, К- 50 и ГЗИП.
Испытание на кручение можно проводить и на других испытательных машинах, имеющих приспособления для поворота одного из захватов машины. Для изменения скручивающегося момента машина должна быть снабжена силоизмерительным устройством
![]()
1,2 - клиновые захваты; 3 - рукоятка;
4 - маховик; 5 - шкала;
6 - барабан; 7 - круговая шкала моментов.
Рисунок 107
Испытательная машина служит для испытания на кручение образцов круглого, прямоугольного и кольцевого поперечных сечений. Длина испытуемых образцов от 130 до 300 мм. Наибольший момент 490 Н∙м. Испытуемый механизм закрепляют в клиновых захватах 1 и 2. Для установки образца нижний захват 2 можно перемещать вверх или вниз с помощью маховика 4, при этом следят за тем, чтобы головки образца вошли в центровые гнезда захватов. Это обеспечит правильное центрирование образца. Скручивание образца осуществляют поворотом нижнего захвата 2. Вращение этого захвата производит электродвигатель через систему передач. Вращение нижнего захвата можно осуществлять вручную с помощью рукоятки 3.
Момент, скручивающий образец, измеряется маятниковым силоизмери -телем, связанным с верхним захватом. Вращение нижнего захвата передается через образец верхнему захвату 1. Поворот верхнего захвата передается на маятник. Момент, скручивающий образец, увеличивается по мере отклонения маятника (рычага с грузом) от вертикального положения. Значение момента определяют по круговой шкале моментов 7. На этой шкале кроме рабочей имеется дополнительная стрелка, которая фиксирует максимальный момент в процессе испытания. На маятнике машины могут быть установлены три различных груза, в зависимости от которых машину можно настроить на нужное значение скручивающего момента: 490 Н∙м, 196 Н∙м, 98 Н∙м.
В зависимости от установленных на маятнике грузов измерения производят по соответствующим шкалам. Для того чтобы избежать резкого падения маятника после разрушения образца, в машине установлен масляный амортизатор.
Угол закручивания образца равен углу поворота нижнего захвата относительно верхнего, отсчет его производят по шкале 5. Для более точного измерения углом поворота на испытуемый образец устанавливают угломер с индикатором часового типа.
Для автоматической записи диаграммы деформации образца в координатах «угол закручивания - вращающий момент» машина снабжена барабаном 6 и пишущим устройством. Вращение нижнего захвата передается на барабан 6, а отклонение маятника, пропорциональное моменту, перемещает карандаш вдоль оси барабана. На бумаге, закрепленной на барабане, вычерчивается кривая зависимости момента от угла поворота нижнего захвата.
28.3 Форма и размеры образцов
На кручение испытывают образцы цилиндрической формы, изготовляемые в соответствии с требованием ГОСТ 3565 - 58. Цилиндрические образцы диаметром 10мм и расчетной длинной 100 мм называют нормальными. ГОСТ допускает испытание пропорциональных образцов с другими размерами. Выбор их размеров зависит от величины предельного момента испытательной машины. Форму и размеры головок образцов выбирают в зависимости от способа крепления в зажимах испытательной машины.
28.4 Порядок выполнения работы
а) измерить диаметр образца d, мм;
б) подготовить диаграммный аппарат к работе, закрепив на нем бумагу;
в) закрепить в захватах машины стальной образец, при этом проследить за надежностью крепления головок образца в захватах, чтобы не было проскальзывания;
г) включить электродвигатель (или вручную), записывать результаты испытания, довести образец до разрушения;
д) вынуть части разрушенного образца и рассмотреть место поломки, определяя характер разрушения;
е) обработать результаты испытания;
ж) по характеру поломки образца определить причину разрушения (произошел ли при разрушении сдвиг или отрыв частиц материала), т.е. выявить, какие напряжения для данного материала наиболее опасны. По значению углы закручивания, при котором произошло разрушение образца, определить пластичность материала.
28.5 Отчет о работе
Тема: Испытание на кручение стального образца
Цель работы- определить пределы прочности материала при кручении и выявить характер разрушения образца.
Оборудование и принадлежности испытательная машина КМ - 50, штангенциркуль, вычислительная машинка.
Ход работы
1 Определить полярный момент сопротивления W ρ, мм 3 по формуле
![]() ;
;
2 Записывать тип машины, цену деления шкалы силоизмерительного устройства и шкалы для измерения угла закручивания;
3 Оформить таблицу записи результатов испытаний;
Таблица 31 - Результаты испытания
|
М, Н∙мм |
|
|
|
|
|
|
|
|
|
φ, град |
|
|
|
|
|
|
|
|
4 По полученным результатам испытания построить диаграмму М -φ;
5 Вычислить условный предел прочности при кручении τпч, МПа, для стального образца.
6
![]() ,
,
где М maх - разрушающий момент из диаграммы М - φ;
7 Выводы о свойствах материала;
8 Ответить на контрольные вопросы.
28.6 Контрольные вопросы
а) какие напряжения возникают при кручении образца в плоскостях, перпендикулярных к его оси; в плоскостях расположенных под углом 450 к его оси?
б) как по характеру разрушения образца определить, какой вид напряжения наиболее опасен для данного материала?
в) что можно сказать о свойстве материала, если разрушение образца произошло в плоскости, расположенной под углом 45 0 к его оси?
г) какой вид имеет поверхность излома чугунного и стального образцов?
д) чем отличаются формулы для подсчета условного предела прочности при кручении для образцов из пластичных и хрупких материалов?
е) при испытании было установлено, что один образец разрушился при угле закручивания 60 0, а другой – при угле 500 0. Сравнить пластичность испытуемых материалов.
28.7 Литература:[2] с.180-192; [3] с.80 - 90; [9] с.216 -238; [6] с.96 -100.
29 САМОСТОЯТЕЛЬНАЯ РАБОТА 19
Тема: Кручение
Выполнение расчетно-графической работы 7
После выполнения самостоятельной работы студент должен:
- иметь представление о деформации при кручении, о кручении круглого цилиндра, о напряженном состоянии в точке, о рациональных формах поперечного сечения и рациональном расположении колес на валу, о моменте сопротивления при кручении;
- знать внутренние силовые факторы при кручении, распределение напряжений по сечению, формулу для расчета напряжения в точке поперечного сечения, деформации при кручении, закон Гука при сдвиге, условия прочности и жесткости при кручении;
- уметь строить эпюры крутящих моментов; производить проектные расчеты валов, работающих на кручение.
29.1 Рекомендуемая последовательность для выполнения
расчетно-графической работы 7
а) определить значения внешних скручивающих моментов М 1, М 3, М 4, соответствующие передаваемым мощностям Р 1, Р 3, Р 4.
б) определить уравновешивающий момент М 2.
в) вычислить крутящие моменты на отдельных участках М z.
г) построить эпюру М z.
д) определить диаметр вала из условий прочности и жесткости.
29.2 Задание для самостоятельной работы 19
Для стального вала постоянного поперечного сечения в соответствии с рисунком 108:
- определить значения моментов М 1, М 2, М 3, М 4;
- определить диаметр вала из расчетов на прочность и жесткость.
Принять [τ k] = 30 МПа, [φ 0] = 0,02 рад / м.
Данные своего варианта взять из таблицы 32.
Окончательно принимаемое значение диаметра вала должно быть округлено до ближайшего большего четного или оканчивающегося на пять числа.
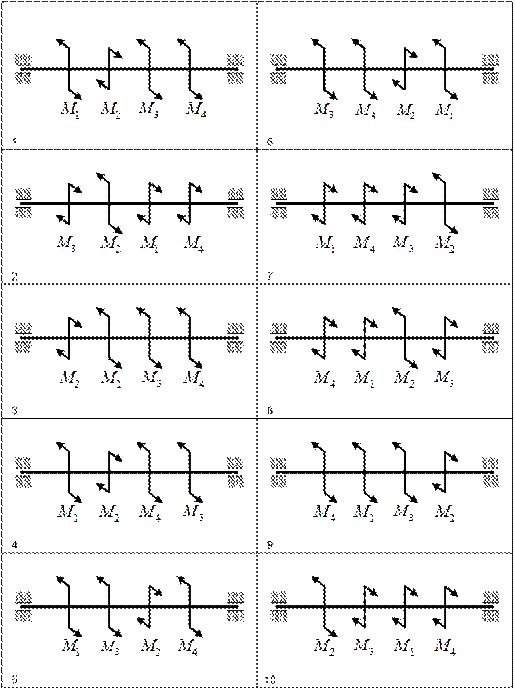
Рисунок 108 – Схемы для выполнения расчетно-графической работы 7
Таблица 32 – Данные для выполнения расчетно-графической работы 7
|
Схема в оответствии с рисунком 108 |
Вариант |
Мощность, кВт |
Угловая скорость, с -1 |
||
|
Р1 |
Р3 |
Р4 |
w |
||
|
1 |
25 12 30 |
35 150 40 |
20 10 25 |
15 50 20 |
20 45 25 |
|
2 |
01 13 24 |
130 100 90 |
90 65 45 |
40 25 20 |
45 35 20 |
|
3 |
02 15 27 |
15 75 55 |
10 80 65 |
35 25 25 |
16 40 20 |
|
4 |
03 14 26 |
60 150 95 |
40 10 70 |
20 75 45 |
20 55 35 |
|
5 |
05 17 29 |
100 50 40 |
18 15 12 |
50 25 20 |
20 18 20 |
|
6 |
04 16 28 |
60 45 50 |
15 10 10 |
80 60 75 |
55 30 30 |
|
7 |
07 19 21 |
18 16 20 |
35 30 35 |
40 45 100 |
10 12 25 |
|
8 |
06 18 20 |
20 40 65 |
50 10 14 |
30 55 80 |
10 16 35 |
|
9 |
09 11 23 |
52 30 35 |
10 0 80 |
60 45 50 |
32 15 18 |
|
10 |
08 10 22 |
80 75 42 |
95 12 60 |
75 90 55 |
25 30 18 |
29.3 Контрольные вопросы
а) что такое чистый сдвиг и какой величиной характеризуется деформация сдвига?
б) как определяют напряжение при кручении в любой точке круглого поперечного сечения бруса и наибольшее напряжение?
в) сформулируйте закон Гука для сдвига;
г) какой физический смысл модуля сдвига G?
д) как нужно нагрузить брус, чтобы он работал только на кручение?
е) на каких гипотезах и допущениях основаны выводы расчетных зависимостей при кручении?
ж) какая зависимость существует между передаваемой валом мощностью, вращающим моментом и угловой скоростью?
з) как определяется крутящий момент в поперечном сечении?
и) сформулируйте правило знаков при определении крутящего момента;
к) во сколько раз увеличится жесткость и прочность бруса круглого поперечного сечения при условии увеличения его диаметра в два раза?
29.4 Литература: [2] с.180 - 192; [3] с.80 - 90; [9] с.216 - 238.
30 ПРАКТИЧЕСКАЯ РАБОТА 6
Тема: Изгиб
После выполнения практической работы студент должен:
- знать виды изгиба и внутренние силовые факторы; порядок построения и контроля эпюр поперечных сил и изгибающих моментов; условие прочности;
- уметь строить эпюры поперечных сил и изгибающих моментов; выполнять проектные и проверочные расчеты на прочность; выбирать рациональные формы поперечных сечений; работать со справочной литературой.
30.1 Тестовый контроль
а) в поперечном сечении балки возникли изгибающий момент Мх и поперечная сила QУ. Укажите вид изгиба.
1) чистый изгиб; 2) поперечный изгиб.
б) поперечные силы в сечении на расстоянии z от концов балок выражены уравнениями
Q 1 = - P ; Q 2 = - P + q × z
Укажите, какими линиями очерчены эпюры поперечных сил.
1) в обоих случаях прямыми линиями;
2) в первом случае - прямой, параллельной оси балки, а во втором
случае - прямой, наклонной к оси балки.
в) изгибающие моменты в сечении на расстоянии z от концов балок выражены уравнениями
М1 = ![]() ;
M2 = M.
;
M2 = M.
Укажите, какими линиями очерчены эпюры изгибающих моментов.
1) в обоих случаях прямыми линиями;
2) в первом случае - прямой, наклоненной к оси, а во втором
случае – прямой, параллельной оси.
г) могут ли быть «скачки» на эпюре изгибающих моментов Мх, если балка нагружена сосредоточенными силами и распределенной нагрузкой?
1) могут;
2) не могут.
д) возможен ли чистый изгиб на протяжении всего участка балки, находящегося под действием равномерно распределенной нагрузки?
1) возможен; 2) не возможен.
е) можно ли считать, что некоторый слой, находящийся между растянутыми и сжатыми волокнами балки, сохраняют первоначальную длину?
1) можно; 2) нельзя.
ж) справедливо ли допущение о том, что поперечные сечения остаются плоскими и при деформации балки?
1) справедливо; 2) не справедливо.
з) до какой величины нормального напряжения справедлив закон Гука при изгибе?
1) до предела текучести; 2) до предела пропорциональности;
3) до предела прочности.
и) во сколько раз уменьшатся нормальные напряжения в прямоугольном сечении балки, если ее высота увеличится в два раза?
1) в два раза; 2) в четыре раза; 3) в восемь раз.
к) зависят ли величины нормальных напряжений от формы поперечных сечений балки?
1) зависит;
2) не зависит.
30.2 Расчетные формулы и правила построения эпюр
Распределение нормальных напряжений при изгибе
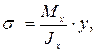
где ![]() -
нормальное напряжение при изгибе, Па;
-
нормальное напряжение при изгибе, Па;
М х – изгибающий момент, Нм;
у – расстояние от рассматриваемой точки до нейтральной оси, м;
J x - осевой момент инерции сечения, м 4.
Условие прочности для балок с сечениями, симметричными относительно нейтральной оси
![]() ,
,
где ![]() -
максимальное нормальное напряжение при изгибе, Па;
-
максимальное нормальное напряжение при изгибе, Па;
М х maх – максимальный изгибающий момент, Нм;
W x - осевой момент сопротивления сечения, м 3;
![]() - допускаемое напряжение
при изгибе, Па.
- допускаемое напряжение
при изгибе, Па.
Для подбора сечения балки (проектного расчета) из условия прочности определяют необходимое значение осевого момента сопротивления:
Wx = ![]()
По найденному значению моменту сопротивления W x подбирают соответствующее сечение по сортаменту или вычисляют размеры прямоугольника, круга.
Знаки поперечных сил Q У и изгибающих моментов М х
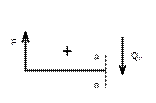
Рисунок 109
Правила построения эпюр.
Для эпюры поперечных сил:
1 На участке, нагруженном равномерно распределенной нагрузкой, эпюра изображается прямой, наклоненной к оси балки.
2 На участке, где приложена сосредоточенная сила, эпюра изображается прямой, параллельной оси балки.
З В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не изменяет значения.
4 В сечении, где приложена сосредоточенная сила, значение поперечной силы меняется «скачкообразно» на значение, равное приложенной силе.
5 В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении. Если в концевом сечении балки не приложена сосредоточенная сила, то поперечная сила в этом сечении равна нулю.
Для эпюры изгибающих моментов:
1 Ha участке, нагруженном равномерно распределенной нагрузкой, эпюра моментов изображается квадратичной параболой. Выпуклость параболы направлена навстречу нагрузке.
2 На участке, свободном от равномерно распределенной нагрузки, эпюра моментов изображается прямой линией.
З В сечении балки, где приложена сосредоточенная пара сил, изгибающий момент меняется “скачкообразно” на значение, равное моменту приложенной пары.
4 Изгибающий момент в концевом сечении балки равен нулю, если в нем не приложена сосредоточенная пара сил. Если же в концевом сечении приложена активная или реактивная пара сил, то изгибающий момент в сечении равен моменту приложенной пары.
5 На участке, где поперечная сила равна нулю, балка испытывает чистый изгиб, и эпюра изгибающих моментов изображается прямой, параллельной оси балки.
6 Ha участке, нагруженном равномерно распределенной нагрузкой, изгибающий момент принимает экстремальное значение в сечении, где эпюра поперечных сил проходит через нуль, меняя знаки с «плюса» на «минус» или с «минуса» на «плюс».
30.3 Последовательность решения задачи
1 Определить опорные реакции.
2 Балку разделить на участки по характерным сечениям.
3 Определить вид эпюры поперечных сил на каждом участке в зависимос- ти от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюры поперечных сил.
4 Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюры изгибающих моментов.
5 Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т.е. определить Wx в опасном сечении, где изгибающий момент имеет наибольшее по модулю значение.
30.4 Пример 1. Проектный расчет (выбор двутавра)
Для заданной консольной балки (рисунок 110) построить эпюры Q y, M x и подобрать двутавровое сечение по ГОСТ 8239 – 72, если:
[s] = 160 МПа, F 1 = 2 кН, F 2 = 1 кН, М = 12 кНм.
Решение
1 Делим балку на участки по характерным сечениям А, В, С
2 Определяем значения поперечной силы Q y и строим эпюру.
1 участок: QУ1 = - F2 ; QУ1 = - 1 кН;
2 участок : QУ2 = - F2 + F1; QУ2 = - 1 + 2 = 1 кН.
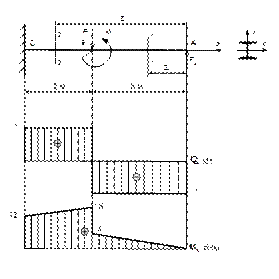
Рисунок 110
3 Определяем значения изгибающих моментов Мх в характерных сечениях и строим эпюру Мх (рисунок 110).
1
участок: М х 1
= ![]() ,
,
при z 1 = 0; М х А = 0;
при
z 1 = 3
м; М х В =![]() кН×м.
кН×м.
2 участок :
М х 2 =
![]() ;
;
при z 2 = 3 м; М х В = 15 кН×м;
при z 2 = 5 м; М х С = 13 кН×м. 4 Исходя из эпюры изгибающих моментов, определим М х maх
М х maх =![]() =
= ![]()
5 Вычисляем
осевой момент сопротивления сечения, исходя из условия прочности : Wx ³ ![]() ; Wx
=
; Wx
= ![]() ;
;
В соответствии с ГОСТ 8239 -72 выбираем двутавр № 16, W x mаб=109 см 3.
Вычисляем недогрузку ![]() :
:
![]() =
= ![]() ;
;
![]() =
=![]() .
.
30.5 Пример 2. Проектный расчет (определение размеров
прямоугольника и круга)
Для заданной двухопорный балки определить реакции
опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры
поперечного сечения (h, b, d) в форме прямоугольника или круга, приняв для прямоугольника ![]() = 1,5.
= 1,5.
Дано: [s] = 160 МПа, F1 = 18 кН, F 2 = 30 кН, М1 =20 кН×м, М2=10 кН×м
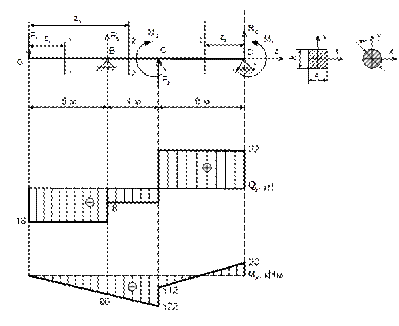
Рисунок 111
Решение
1 Определяем опорные реакции и проверяем их найденные значения
å М д
= 0; å М д = – M1 + ![]() +
М2 +
+
М2 + ![]() –
– ![]() = 0;
= 0;
Rв = ![]() ; Rв
=
; Rв
= ![]() кН.
кН.
å М В = 0; å М В = – M1
– ![]() + М2 –
+ М2 – ![]() –
– ![]() =
0;
=
0;
RD = ![]() ;
RD =
;
RD = ![]() кН.
кН.
Проверка: ΣFкy = – F1 + Rв + F2 – RD = 0; ΣFкy = – 18 + 10 + 30 – 22 = 0
Условие равновесия ΣFкy = 0 - выполняется.
2 Делим балку на участки по характерным сечениям О, В, С, D.
3 Определяем в характерных сечениях значения поперечной силы и строим эпюру QУ слева направо
1 участок: Q У1 = - F1; Q У1 = - 18 кН;
2 участок : Q У2 = - F1 + RВ; Q У2 = - 8 кН;
3 участок : Q У3 = - RD; Q У3 = 22 кН.
4 Вычисляем в характерных сечениях значения изгибающего момента М х и
строим эпюру М х
. 1 участок: М х
1 = - ![]() ;
;
при z 1 = 0; М х О = 0;
при z 1 = 5
м; М х В = ![]() кН×м.
кН×м.
2 участок : М х 2 = ![]() ;
;
при z 2 = 5 м; М х В = - 90 кН×м;
при z2 = 9 м; Мх С = - 122 кН×м.
3 участок : М х
3 = ![]() ;
;
при z 3 = 0; М х D = 20 кН×м;
при z3 = 6 м; М х С = -112 кН×м.
5 Вычисляем осевой момент сопротивления сечения, исходя из условия прочности при изгибе
Wx = ![]() =
= ![]() ; Wx
=
; Wx
= ![]() мм 3 .
мм 3 .
6 Определяем размеры прямоугольного сечения балки
Wx = ![]() ;
;
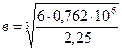 = 127
мм.
= 127
мм.
Принимаем ![]() мм; h =
мм; h = ![]() мм.
мм.
7 Определяем размеры круглого сечения
Wx = 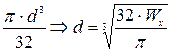 ;
; 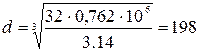 мм.
мм.
Принимаем d = 200 мм
30.6 Задание для бригад
Для заданной
двутавровой балки построить эпюры Q У, М
х и подобрать сечение по сортаменту, если: Р = 10 кН, ![]() = 2
м, М = 5 кНм, [s] = 160 МПа.
= 2
м, М = 5 кНм, [s] = 160 МПа.
|
|
|
|
|
|
|
|
|
Рисунок 112
30.7 Литература: [2] с.201 - 219, 221 - 223; [3] с.91 - 110;
31 САМОСТОЯТЕЛЬНАЯ РАБОТА 20
Тема: Изгиб
Выполнение расчетно-графической работы 8.
После выполнения самостоятельной работы студент должен:
- иметь представление о дифференциальных зависимостях при изгибе;
- знать виды изгиба и внутренние силовые факторы, порядок построения и контроля эпюр поперечных сил и изгибающих моментов, условия прочности и жесткости;
- уметь строить эпюры; выполнять проектный расчет; выбирать рациональные формы поперечных сечений.
31.1 Рекомендуемая последовательность для выполнения
расчетно-графической работы 8
а) определить опорные реакции и проверить их найденные значения;
б) делить балку на участки, определить продольные силы, изгибающие моменты на отдельных участках;
в) построить эпюры продольных сил и изгибающих моментов;
г) вычислить (подобрать) размер сечения из условия прочности.
31.2 Задание для самостоятельной работы 20
Задача 1. Для заданной двухопорной балки в соответствии с рисунком
113 определить реакции опор, построить эпюры поперечных сил,
изгибающих моментов; подобрать из условия прочности размеры поперечного сечения
балки, приняв для прямоугольника ![]() , если
[σ] = 160 МПа.
, если
[σ] = 160 МПа.
Задача 2. Для стальной балки, жестко защемленной одним концом и нагруженной в соответствии с рисунком 114, построить эпюры поперечных сил, изгибающих моментов; подобрать из условия прочности необходимый размер двутавра, приняв [σ] = 150 МПа.
Данные своего варианта для задач 1, 2 брать из таблицы 33, 34.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 113 – Схемы для выполнения задачи 1
Таблица 33 – Данные для выполнения задачи 1
|
Схема в соответствии с рисунком 113 |
Вариант |
Сила, кН |
Момент, кН×м |
|
|
F1 |
F2 |
М |
||
|
1 |
30 15 29
|
20 12 10 |
10 8 20 |
12 20 15 |
|
2 |
01 14 28
|
2 14 20 |
6 5 14 |
10 8 10 |
|
3 |
02 17 21
|
5 12 10 |
20 16 20 |
4 5 30 |
|
4 |
03 16 20
|
10 1 2 |
15 6 10 |
2 8 3 |
|
5 |
05 19 23
|
20 15 30 |
1 2 4 |
2 3 1 |
|
6 |
04 18 22
|
3 5 12 |
2 4 16 |
10 8 5 |
|
7 |
07 11 25
|
5 8 10 |
2 1 2 |
6 4 5 |
|
8 |
06 10 24
|
1 4 2 |
2,5 3 4,5 |
2 10 6 |
|
9 |
09 12 27
|
2 4 6 |
4 1,5 2 |
1 10 12 |
|
10 |
08 13 26
|
6,5 1 3,5 |
1,4 2 8 |
2 14 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 114 – Схемы для выполнения задачи 2
Таблица 34 – Данные для выполнения задачи 2
|
Схема в соответствии с рисунком 114 |
Вариант |
Сила, кН |
Момент, кН×м |
Интенсивность распределенной нагрузки, кН / м |
|
F |
M |
q |
||
|
1
|
30 13 27 |
20 30 40 |
10 20 10 |
10 20 20 |
|
2 |
01 15 26 |
10 30 40 |
40 30 30 |
10 20 20 |
|
3
|
02 14 29 |
20 30 10 |
10 10 10 |
10 10 10 |
|
4 |
03 17 28 |
20 30 40 |
10 10 10 |
10 10 20 |
|
5
|
05 16 21 |
10 10 20 |
10 10 10 |
10 20 20 |
|
6 |
04 19 20 |
30 40 50 |
10 10 10 |
10 10 10 |
|
7
|
07 18 23 |
10 20 20 |
10 10 10 |
10 10 20 |
|
8
|
06 11 22 |
10 20 20 |
10 10 20 |
10 10 20 |
|
9
|
09 10 25 |
20 30 30 |
10 10 10 |
10 10 20 |
|
10 |
08 12 24 |
10 20 30 |
10 10 10 |
10 10 10 |
31.3 Контрольные вопросы
а) какие внутренние силовые факторы возникают в поперечных сечениях бруса при его прямом поперечном изгибе? чистом изгибе?
б) что называется поперечной силой в поперечном сечении бруса и чему она численно равна?
в) что такое эпюра поперечных сил и как она строится?
г) что называется изгибающим моментом в поперечном сечении бруса?
д) сформулируйте правило знаков для поперечных сил и изгибающих моментов;
е) каков характер деформаций, возникающих при изгибе?
ж) что такое жесткость сечения при изгибе?
з) что такое осевой момент сопротивления и какова его единица измерения?
и) зависит ли возникающее при изгибе нормальное напряжение:
1) от материала балки;
2) от формы поперечного сечения;
к) во сколько раз изменится прочность балки при прочих равных условиях, если:
1) увеличить диаметр балки в два раза;
2) увеличить в два раза длину консольной балки, нагруженной силой на конце консоли?
л) какая геометрическая характеристика сечения характеризует его прочность при изгибе?
м) относительно какой оси повернется поперечное сечение балки и какая ось сечения будет нейтральной, если балка нагружена силой по направлению оси У?
31.4 Литература: [2] с.201 - 219, 221 - 223; [3] с.91 - 110;
32 САМОСТОЯТЕЛЬНАЯ РАБОТА 21
Тема: Сложное сопротивление
Выполнение расчетно-графической работы 9
После выполнения самостоятельной работы студент должен:
- иметь представление о сложном сопротивлении, о теории предельных напряженных состояний, об эквивалентном напряженном состоянии, о гипотезах прочности;
- знать формулы для эквивалентных напряжений по гипотезам наибольших касательных напряжений и потенциальной энергии формоизменения;
- уметь составлять расчетные схемы и рассчитывать брус круглого поперечного сечения на прочность при сочетании основных деформаций, работать со справочной литературой.
32.1 Рекомендуемая последовательность для выполнения расчетно-графической работы 9
а) составить расчетную схему вала, приводя действующие на вал нагрузки к оси;
б) определить вращающий момент, действующий на вал: М 1 = М 2 = Р / ω;
в) вычислить нагрузки, приложенные к валу:
F 1 = 2×M 1/ d 1, F2 = 2×M 2 / d2, F r1 = 0,4 F1, F r2 = 0,4×F2.
г) определить реакции опор в вертикальной плоскости уОz и в горизонтальной плоскости хОz;
д) построить эпюру крутящих моментов Мz;
е) определить ординаты и построить эпюры изгибающих моментов Мх - в вертикальной плоскости, Му - в горизонтальной плоскости;
ж) определить суммарные значения изгибающих моментов;
з) вычислить значение эквивалентного момента для опасного сечения;
и) определить требуемый размер вала.
32.2 Задание для самостоятельной работы 21
Для стального вала постоянного поперечного сечения с двумя зубчатыми колесами, передающего мощность Р, кВт, при угловой скорости ω, рад/с:
а) определить вертикальные и горизонтальные составляющие реакции подшипников;
б) построить эпюру крутящих моментов;
в) построить эпюру изгибающих моментов в вертикальной и горизонтальной плоскостях;
г) определить диаметр вала, приняв [σ] = 60 МПа. Расчет производить по гипотезе потенциальной энергии формоизменения, если Fr1 = 0,4 F1; Fr2 = 0,4 F2.
Таблица 35 – Данные для выполнения расчетно-графической работы 9
|
Схема в соответствии с рисунком 115 |
Вариант |
Мощность, кВт |
Угловая скорость, с -1 |
|
Р |
ω |
||
|
1
|
30 14 26 |
6 8 10 |
22 36 40 |
|
2 |
01 17 29 |
3 8 10 |
25 48 50 |
|
3
|
02 16 28 |
10 20 15 |
30 80 45 |
|
4 |
03 19 21 |
5 6 7 |
40 36 35 |
|
5
|
05 18 20 |
5 10 12 |
18 18 30 |
|
6 |
04 11 23 |
20 19 21 |
45 38 15 |
|
7
|
07 10 22 |
4 20 18 |
35 15 20 |
|
8
|
06 12 25 |
16 30 28 |
40 50 42 |
|
9
|
09 13 24 |
12 15 10 |
38 42 32 |
|
10 |
08 15 27 |
40 30 32 |
70 50 38 |
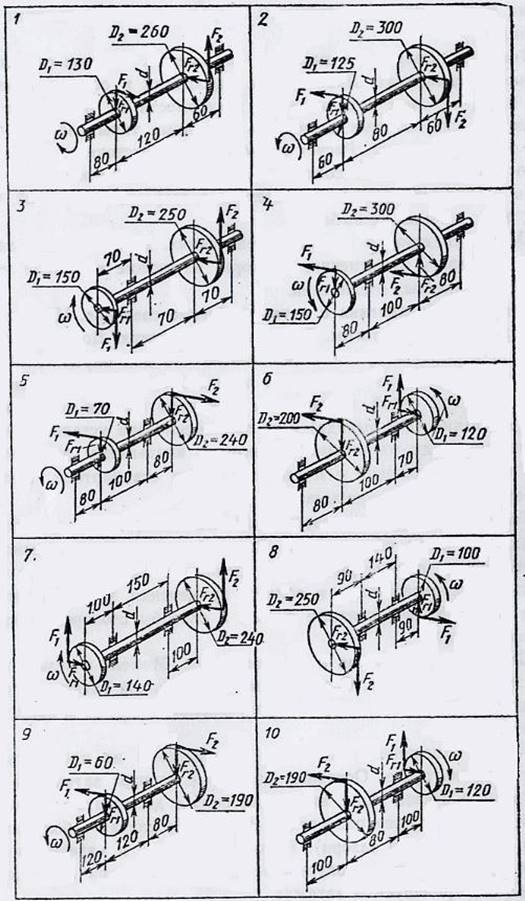
Рисунок 115 – Схемы для выполнения расчетно-графической работы 9
32.3 Контрольные вопросы:
а) какие внутренние силовые факторы возникают в поперечном сечении деталей, работающих на совместное действие изгиба и кручения?
б) что такое гипотезы прочности и в каких случаях их применяют?
в) как производится расчет валов на прочность при совместном действии изгиба и кручения?
г) что такое эквивалентное напряжение?
д) какой вид имеет выражение эквивалентного напряжения при совместном действии изгиба и кручения по гипотезе потенциальной энергии формоизменения?
е) что такое эквивалентный момент и как его определить?
ж) что такое суммарный изгибающий момент?
з) во сколько раз изменится прочность вала, испытывающего кручение и изгиб, если его диаметр увеличится в 2 раза?
и) вычислите эквивалентный момент по теории наибольших касательных напряжений, приняв для опасного сечения вала: Мх = 400 Нм и Мz = 300 Нм. Определите диаметр вала, приняв [σ] = 100 МПа;
к) какие точки поперечного сечения вала, испытывающего кручение и изгиб, являются опасными? Для каких точек сечения эквивалентные напряжения вычисляют по формуле: σ экв = М экв /Wх.
32.4 Литература: [2] с.240 - 243; [3] с.112 - 118; [9] с.278 - 289.
33 САМОСТОЯТЕЛЬНАЯ РАБОТА 22
Тема: Сопротивление усталости
Изучение вопроса «Определение коэффициента запаса прочности вала при сочетании деформаций «Кручение и изгиб».
После выполнения самостоятельной работы студент должен:
- иметь представление об усталости материалов;
- знать факторы, влияющие на сопротивление усталости; основы расчета на прочность при переменном напряжении.
33.1 Задание для самостоятельной работы 22
Изучить теоретический материал и составить конспект, раскрывая следующие понятия:
а) усталостное разрушение, его причины и характер;
б) факторы, влияющие на величину предела выносливости;
в) коэффициент запаса прочности вала при сочетании деформаций «Кручение и изгиб».
33. 2 Контрольные вопросы
а) что называется усталостным разрушением или усталостью материала? каковы его причины?
б) как определяется коэффициент запаса прочности вала при переменных напряжениях?
в) что такое концентрация напряжений и в чем причина ее возникновения?
г) какие факторы влияют на снижение предела выносливости?
д) что называется пределом выносливости материала и от чего он зависит?
е) каково влияние абсолютных размеров детали на предел выносливости?
ж) как производится проверочный расчет на прочность (определение фактического коэффициента запаса) при переменных напряжениях?
33.3 Литература: [2] c. 243 - 251; [3] с.123 - 127; [5] с.285 - 308.
34 САМОСТОЯТЕЛЬНАЯ РАБОТА 23
Тема: Прочность при динамических нагрузках
Изучение вопроса «Приближенный метод расчета на удар».
После выполнения самостоятельной работы студент должен:
- иметь представление о допущениях при расчетах на действие ударных нагрузок, о приближенном методе расчета на удар;
- знать приближенный метод расчета на прочность при ударе.
34.1 Задание для самостоятельной работы 23
Изучить теоретический материал и составить конспект, раскрывая следующие понятия:
а) ударное действие нагрузки;
б) расчетная модель и основные допущения;
в) формула динамического коэффициента;
г) приближенный учет распределенной массы стержня при ударе.
34. 2 Контрольные вопросы
а) что такое удар?
б) какие допущения используются при определении динамического коэффициента при вертикальном ударе?
в) запишите формулу для динамического коэффициента при ударе;
г) объясните влияние на динамический коэффициент при ударе массы ударяемого груза;
д) как учитывается распределенная масса стержня с помощью коэффициента приведения и из каких соображений он определяется?
34.3 Литература: [4] c. 252 - 253; [5] с.342 - 349; [8] с.472 - 481.
35 САМОСТОЯТЕЛЬНАЯ РАБОТА 24
Тема: Устойчивость сжатых стержней
Выполнение расчетно-графической работы 10.
После выполнения самостоятельной работы студент должен:
- иметь представление о критическом напряжении, о гибкости стержня, о предельной гибкости;
- знать условие устойчивости сжатых стержней, формулу Эйлера и эмпирические формулы для расчета критической силы и критических напряжений;
- уметь определять допускаемую нагрузку, проводить проверку сжатых стержней на устойчивость, работать со справочной литературой.
35.1 Рекомендуемая последовательность для выполнения
расчетно-графической работы 10
а) определить радиус инерции сечения;
б) определить гибкость стержня;
в) определить критическую силу;
г) определить допускаемую силу.
35.2 Задание для самостоятельной работы 24
Для сжатого стержня длиной ℓ = 3 м в соответствии с рисунками 116, 117, 118 определить допускаемое значение силы Р, если нормативный коэффициент запаса устойчивости [n y] = 2.
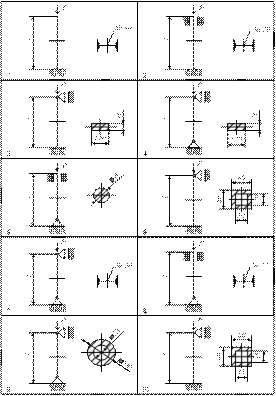
Рисунок 116 – Схемы 1…10
![]()
Рисунок 117– Схемы 11…20
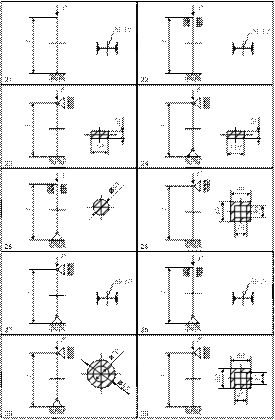
Рисунок 118– Схемы 21…30
35.3 Контрольные вопросы
а) в каком случае происходит потеря устойчивости сжатого стержня?
б) какая сила называется критической?
в) какой вид имеет формула Эйлера для критической силы при различных случаях закрепления стержня?
г) какова зависимость между критическим и допускаемым значениями сжимающей силы?
д) что называется гибкостью стержня?
е) в каких пределах применима формула Эйлера?
ж) в каком случае расчет стойки на устойчивость ведут по формуле Ясинского?
з) каковы наиболее рациональные формы поперечных сечений сжатых стержней?
и) во сколько раз изменится значение критической силы для стержня большой гибкости, если:
1) длину стержня увеличить в 2 раза;
2) диаметр стержня уменьшить в 2 раза;
к) какое практическое значение имеет определение критической силы сжатых стержней?
35.4 Литература: [2] c. 251 - 256; [3] с.119 - 123; [9] с.289 - 300.
ЛИТЕРАТУРА
Основная
1. ГОСТ 2.105-95 Общие требования к текстовым документам.
2. Мовнин М.С., Израелит А.Б. Рубашкин А.Г. Основы технической механики. СПб., Политехника, 2003. 286 c.
3. Ицкович Г.М. Сопротивление материалов. М., Высшая школа, 2001. 368с.
4. Рубашкин А.Г., Чернилевский Д.В. Лабораторно – практические работы по технической механике. М., Высшая школа, 1975. 254с.
5. Олофинская В.П. Техническая механика курс лекций с вариантами практических и тестовых заданий. М., ФОРМ: ИНФРА - М, 2003. с. 349.
Дополнительная
6. Покровский В.Е., Столярчук А.И. Техническая механика.
Kонтрольные задания. М., Высшая школа, 1986. 159 с.
7. Мовнин М.С., Израелит А.Б., Рубашкин А.Г. Основы технической механики. Л., Судостроение, 1973. 576 с.
8. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. М., Высшая школа, 2000. 560 с.
9. Олофинская В.П. Т ехническая механика. М., ФОРУМ - ИНФРА - М, 2003. 349 с.
10. Олофинская В.П. Техническая механика. Сборник тестовых заданий М., ФОРУМ-ИНФРА-М, 2002. 132с.
11. Cетков В.И. Сборник задач по технической механике. М., Академия, 2003. 224 c.
11. Аркуша А.И., Фролов М.И. Техническая механика. М., Высшая школа, 1983. 447 c.
12. Эрдеди А.А. и др. Техническая механика М., Высшая школа, 1980 446с.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.