
Филиал бюджетного профессионального образовательного учреждения Чувашской Республики
«Чебоксарский медицинский колледж»
Министерства здравоохранения Чувашской Республики в городе Канаш
|
РАССМОТРЕНО и ОДОБРЕНО на заседании ЦМКОГСЭ Протокол № ____ «____» _______________ 20 ___ г. Председатель ЦМК
|
утверждено Зав. филиалом БПОУ «ЧМК» МЗ Чувашии в г. Канаш
|
Методическая разработка теоретического занятия
уравнения cos x = a
учебная дисциплина БД. 04 Математика
специальность 34.02.01Сестринское дело
(базовая подготовка)
Канаш, 2025
|
Составитель: Семенова А.М., преподаватель высшей квалификационной категории филиала БПОУ ЧР «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г. Канаш
|
|
Рецензент: Иванова Л.М., преподаватель, высшей квалификационной категории филиала БПОУ ЧР «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г. Канаш
|
Аннотация
Данная разработка предназначена для изучения темы «Уравнение cos x =a» обучающимися 1 курсов СПО. Эта тема является введением в последующие, следовательно, именно ее успешное понимание и отработка послужат базой под изучение других.
Для того чтобы установить связи преемственности в изучении нового материала с изученным, включить новые знания в систему ранее усвоенных, повторяется тема «Тригонометрия», которая подготавливает учащихся к восприятию нового материала.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. методический блок
1.1. Учебно-методическая карта
Формы деятельности
1.2. Технологическая карта
2. Информационный блок
2.1. План лекции
2.2 Текст лекции
2.3. Глоссарий
3. Контролирующий блок
Методическая разработка занятия на тему «Уравнение cos x =a.» из раздела «Тригонометрическая функция» составлена на основе Рабочей программы по математике и календарно-тематического плана. Темы занятия взаимосвязаны содержанием, основными положениями.
Цель изучения данной темы узнать основные тригонометрические тождества, формулы приведения.
Программный материал данного занятия базируется на знаниях математики. Методическая разработка занятия составлена для проведения теоретических занятий по теме: «Уравнение cos x =a.» –2 часа. В процессе практического занятия студенты закрепляют полученные знания: определения функций, их свойства и графики, преобразования графиков, непрерывные и периодические функции, обратные функции и их графики.
Методическая разработка предназначена для оказания методической помощи студентам при изучении занятий по теме «Уравнение cos x =a». Методическая разработка основывается на учебнике для базового и профильного обучения: Алгебра и начала математического анализа Ш.А Алимов.
|
Тема занятия |
Логарифмы. |
||||||
|
Учебная дисциплина |
БД.04 Математика |
||||||
|
Специальность |
34.02.01 Сестринское дело (базовая подготовка) |
||||||
|
Курс |
I |
||||||
|
Группа |
9М-11-20, 9М-12-20, 9М-13-20,9М-14-20, 9М-15-20. |
||||||
|
Место проведения |
Кабинет № 5 |
||||||
|
Продолжительность занятия |
90 мин. |
||||||
|
Характеристика занятия |
Вид |
Вид занятия: Лекция текущая, обзорная.
|
|||||
|
Тип |
Типы учебных занятий урок изучения нового материала; комбинированный урок
|
||||||
|
Форма |
Изложение, рассказ, объяснение с демонстрацией наглядных пособий. Формы деятельностиФронтальная.
|
||||||
|
Технологии обучения |
Традиционная технология обучения
|
||||||
|
Методы обучения |
Метод Репродуктивный: упражнения, действия по алгоритму. Интерактивные методы – практическая отработка осваиваемых знаний, умений, навыков на уровне компетенций
|
||||||
|
Средства обучения |
1.По характеру воздействия на обучаемых: ИКТ - презентации; 2.По степени сложности: простые: учебники, печатные пособия.
|
||||||
|
Методическая цель |
Методическая цель - отрабатывать методику контроля результатов выполнения письменных упражнений. - реализовывать индивидуальный дифференцированный подход в процессе выполнения обучающимися заданий для самостоятельной работы; |
||||||
|
Цели и задачи занятия |
Воспитательная |
Формулировать интеллектуальных, нравственных, эмоционально-волевых качеств у обучающихся.
|
Воспитывать положительное отношение к приобретению новых знаний; Воспитывать ответственность за свои действия и поступки; Вызвать заинтересованность новым для студентов подходом изучения математики. Воспитывать интерес к математике путём введения разных видов закрепления материала: устной работой, работой с учебником, работой у доски, ответами на вопросы и умением делать самоанализ, самостоятельной работой; стимулированием и поощрением деятельности учащихся.
|
||||
|
Образовательная |
Сформирование представлений у студентов понятия простейших тригонометрических уравнений. Обобщение и систематизирование приобретенных знаний по теме Уравнение cos x =a.
|
Закрепить знания при решении тригонометрических уравнений, используя основные тригонометрические тождества; Включить новые знания в систему ранее усвоенных; закрепить изученный на этом уроке. |
|||||
|
Развивающая |
Развитие речи, мышления, сенсорной восприятие внешнего мира через органы чувств сферы;
|
Формировать навыки познавательного мышления. Продолжить развитие умения выделять главное. Продолжить развитие умения устанавливать причинно-следственные связи. Развивать
навыки и умения, в выполнении заданий по теме, умение работать в группе и
самостоятельно. Развивать логическое мышление, правильную и грамотную
математическую речь, развитие самостоятельности и уверенности в своих знаниях
и умениях при выполнении разных видов работ. |
|||||
|
Планируемый результат |
Уметь |
Воспроизвести опорные знания по теме; совершенствовать навыки применения основных тригонометрических формул и формул приведения; формировать навыки решения простейших тригонометрических уравнений; |
|||||
|
Знать |
Методы решения простейших тригонометрических уравнений. |
||||||
|
Формированиекомпетенций у обучающихся |
Общие (ОК)
|
Л1. Сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики; Л5. Готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности; Л8. Отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем; М2. Умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты; М5. Владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
|
|||||
|
Профессиональные (ПК) |
П1. Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке; П3. Владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач; П4. Владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств; |
||||||
|
Межпредметные связи |
Входящие |
Алгебра, тригонометрия. |
Математический анализ. |
||||
|
Выходящие |
Тригонометрическое тождество |
Формулы приведения. |
|||||
|
|
|
||||||
|
|
|
||||||
|
Внутрипредметные |
Синус, косинус, тангенс и котангенс. Формулы приведения. |
||||||
|
|
|||||||
|
Оснащение занятия |
Методическое |
Методическая разработка занятия. |
|||||
|
Материально-техническое |
Ручка, карандаш, тетрадь, линейка. |
||||||
|
Информационное |
Компьютер, интерактивная доска. |
||||||
|
Список литературы |
Основная |
1.Алимов, Ш. А. Алгебра и начала математического анализа (базовый и углубленный уровни)10—11 классы / Ш.А. Алимов — М., 2018. – с.455. 2.Колягин, Ю.М. Математика: алгебра и начала математического анализа. Алгебра и начала математического анализа (базовый и углубленный уровни). 11 класс / М. В Ткачева., Н. Е Федерова. — М., 2018. - 384 с. |
|||||
|
Дополнительная |
1 Александров А.Д., Геометрия / А.Л.Вернер, В.И. Рыжик (базовый и профильный уровни). 10—11 кл. – 2017. – 344 с. 2. Богомолов, И.Д. Математика: учебник / И.Д. Богомолов. – М., 2018. - 384 с.
|
||||||
|
Интернет-ресурсы |
1. Калашникова В.А. Методическое пособие: «Конспекты лекций по математике» [Электронный ресурс] /В.А. Калашникова. 2. Яковлев Г.Н. Алгебра и начала анализа (Математика для техникумов) [Электронный учебник] /Г.Н Яковлев. - Режим доступа: http://lib.mexmat.ru/books/78472. 3.http://fcior.edu.ru/ - Федеральный центр информационно-образовательных ресурсов 4.http://school-collection.edu.ru/ - Единая коллекция цифровых образовательных ресурсов
|
||||||
|
Деятельность преподавателя |
Деятельность обучающихся |
Методическое обоснование |
Формируемые ОК и ПК |
|
|
1. Организационный этап -5 мин. |
||||
|
Проверяет готовность обучающихся к занятию. дает положительный эмоциональный настрой, организует, проверяет готовность уч-ся к уроку |
Готовятся к началу занятия. |
Включение обучающихся в деятельность на личностно значимом уровне. |
ОК 1, ОК 4. П1. |
|
|
2. Этап всесторонней проверки домашнего задания - 10мин. |
||||
|
Выявляет правильность и осознанность выполнения всеми обучающимися домашнего задания; устранить в ходе проверки обнаруженные пробелы в знаниях. |
По очереди комментируют свои решения. Приводят примеры. Пишут под диктовку.
|
Повторение изученного материала, необходимого для открытия нового знания, и выявление затруднений в индивидуальной деятельности каждого обучающегося. |
ОК1, ПК 1, ПК4 |
|
|
3. Постановка цели и задач занятия. Мотивация учебной деятельности обучающихся - 5 мин. |
||||
|
Озвучивает тему урока и цель, уточняет понимание обучающегося поставленных целей урока. Эмоциональный настрой и готовность преподавателя на урок.
|
Эмоционально настраиваются и готовятся обучающихся на урок. Ставят цели, формулируют тему урока. |
Обсуждение затруднений; проговаривание цели урока в виде вопроса, на который предстоит ответить. Методы, приемы, средства обучения: побуждающий от проблемы диалог, подводящий к теме диалог. |
ОК 1, ОК 4. П1. |
|
|
4. Актуализация знаний -30 мин. |
||||
|
Уточняет понимание обучающимися поставленных целей занятия. Выдвигает проблему. Создает условия, чтобы обучающийся смогли систематизировать знания о множестве действительных чисел, имели представление о пределе числовой последовательности
|
Под диктовку, все выполняют задание, а один проговаривает вслух.
|
Создание проблемной ситуации. Уч-ся- фиксируют индивидуальные затруднения. Создание условия, чтобы обучающийся смогли систематизировать знания о множестве действительных чисел. |
ОК 1, ОК 4. П1. |
|
|
5. Первичное усвоение новых знаний- 10 мин. |
||||
|
Создаёт эмоциональный настрой на усвоение новых знаний.
|
Внимательно слушают, записывают под диктовку в тетрадь. |
Создание условий, чтобы обучающийся смогли систематизировать знания о множестве действительных чисел. |
ОК1, ПК 1, ПК4 |
|
|
6. Первичная проверка понимания- 10 мин. |
||||
|
Проводит параллель с ранее изученным материалом. Проводит беседу по уточнению и конкретизации первичных знаний;
|
Отвечают на заданные вопросы преподавателем. |
Осознание степени овладения полученными знаниями - каждый для себя должен сделать вывод о том, что он уже умеет. |
ОК1, ПК 1, ПК4 |
|
|
7. Первичное закрепление- 5 мин. |
||||
|
Контролирует выполнение работы. Осуществляет: индивидуальный контроль; выборочный контроль. Побуждает к высказыванию своего мнения. Показывает на доске решение, опираясь на алгоритм. |
записывают решение, остальные решают на местах, потом проверяют друг друга;
|
Тренировка и активизация употребления новых знаний, включение нового в систему Режим работы: устная, письменная, фронтальная, индивидуальная. |
ОК1, ПК 1, ПК4 |
|
|
8. Контроль усвоения, обсуждение допущенных ошибок и их коррекция (подведение итогов занятия 5 мин |
||||
|
Отмечает степень вовлеченности обучающихся в работу на занятии. Задает вопросы по обобщению материала. |
Под диктовку, все выполняют задание, а один проговаривает вслух; |
Оценивание работу обучающихся, делая акцент на тех, кто умело взаимодействовал при выполнении заданий |
ОК 1, ОК 4. П1. |
|
|
9. Информация о домашнем задании, инструктаж по его выполнению5 мин |
||||
|
Обсуждение способов решения домашнего задания. Записывает номера заданий на доске.
|
Обобщают полученные знания, делают вывод о выполнении задач урока. |
Информация о домашнем задании, инструктаж по его выполнению
|
ОК 1, ОК 4. П1. |
|
|
10. Рефлексия (подведение итогов занятия),5 мин |
||||
|
Акцентирует внимание на конечных результатах учебной деятельности обучающихся на занятии.
|
1. Проводят самоанализ: “Чему научились и что нового узнали?”
|
Осознание своей учебной деятельности; самооценка результатов деятельности своей. |
ОК1, ПК 1, ПК4 |
|
|
№ п/п |
Изучаемые вопросы |
Уровень усвоения |
|
1. |
Объяснение темы Уравнение cos х =а. |
1 |
|
|
1.1 Общее решение уравнения cos x =a. |
2 |
|
|
1.2 Частное решение уравнения. |
2 |
|
2. |
Закрепление нового материала. |
|
|
|
2.1 Примеры и разбор решения заданий тренировочного модуля. |
3 |
|
|
2.2Решение примеров устно. |
|
|
3. |
Решение упражнений (нечетные пункты) на закрепление темы № 620- 627. |
3 |
|
4. |
Домашнее задание № 620-627. (четные пункты). |
3 |
2.2 Текст лекции
Конспект урока
Алгебра и начала математического анализа, 10 класс
Уравнение cos x = a.
Перечень вопросов, рассматриваемых в теме:
·
решение уравнения ![]() для
табличных значений
для
табличных значений
· арккосинус числа, простейшие тождества с арккосинусом
· решение простейших тригонометрических уравнений;
·
решение уравнения вида ![]()
·
решение уравнения вида ![]() ;
;
·
решение уравнения вида ![]() ;
;
· вычисление значений арккосинуса числа.
Глоссарий по теме
Арккосинусом числа m ![]() называется
такое число α, что:
называется
такое число α, что: ![]() и
и ![]() .
.
Арккосинус числа m обозначают: ![]() .
.
Основная литература:
Колягин Ю. М., Ткачёва М. В., Фёдорова Н. Е., Шабунин М. И. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни. Под ред. А.Б. Жижченко. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс.310-314.
Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс. 69-88.
Открытые электронные ресурсы:
2. Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
1.
Решение тригонометрического уравнения ![]() на
первом этапе целесообразно выполнять с использованием тригонометрической
окружности. Из рисунка видно, что при
на
первом этапе целесообразно выполнять с использованием тригонометрической
окружности. Из рисунка видно, что при ![]() ,
таких точек нет, при
,
таких точек нет, при ![]() ,
такая точка одна, при
,
такая точка одна, при ![]() ,
таких точек две.
,
таких точек две.
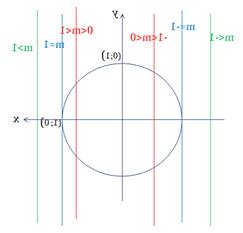
Рисунок 1 – Точки пересечения прямой x = m с тригонометрической окружностью
Рассмотрим решение уравнения ![]() .
.
Прямая ![]() пересекает
тригонометрическую окружность в двух точках:
пересекает
тригонометрическую окружность в двух точках:
M(π/6) и N(-π/6).
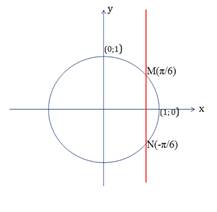
Рисунок 2 – Решение уравнения ![]()
Точка M(π/6) соответствует всем числа вида ![]() .
.
Точка N(-π/6) соответствует всем числа вида ![]() .
.
Таким образом, решение уравнения ![]() можно
записать так:
можно
записать так:
![]() .
.
Ответ: ![]() .
.
Чтобы уметь решать уравнение ![]() для
произвольных значений m, вводится понятие арккосинуса.
для
произвольных значений m, вводится понятие арккосинуса.
Арккосинусом числа m ![]() называется
такое число α, что:
называется
такое число α, что: ![]() и
и ![]() .
.
Арккосинус числа m обозначают: ![]()
Для ![]()
![]()
Если ![]() и
и![]() ,
то
,
то ![]() .
.
Два простейших тождества для арккосинуса.
1.
![]() для
любого m:
для
любого m: ![]()
2.
![]() для
любого α:
для
любого α: ![]()
Из рисунка видно, что ![]() .
.
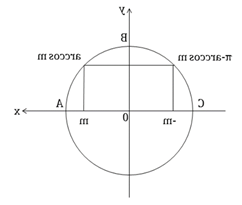
Рисунок 3 – Связь между ![]() и
и ![]()
Решением уравнения ![]() являются
все числа вида
являются
все числа вида
![]()
Примеры и разбор решения заданий тренировочного модуля
№1.Решите уравнение ![]() .
.
В ответ запишите наименьший положительный корень.
Решение:
![]()
![]()
![]()
![]()
При ![]() получаем
получаем ![]() .
.
При увеличении значений k значение первого корня будет отрицательным, а значение второго корня будет увеличиваться.
При уменьшении значений k значение первого корня будет увеличиваться, а значение второго корня будет отрицательным. Поэтому наименьшее положительное значение корня 1.
Ответ: 1
№2.Решите уравнение ![]() .
Определите, сколько решений имеет это уравнение при:
.
Определите, сколько решений имеет это уравнение при:
1. k=-3
Ответ: 0
1. k=0
Ответ: 4
1. k=2
Ответ: 4
Решение:
Запишем решение данного уравнения в виде:
![]()
Тогда: 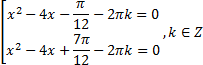
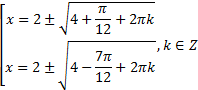
Первое уравнение имеет решение, если ![]() .
То есть
.
То есть ![]() ,
или
,
или ![]() .
.
Второе уравнение имеет решение, если ![]() .
То есть
.
То есть ![]() ,
или
,
или ![]() .
.
Поэтому при ![]() уравнение
будет иметь 4 решения, а при
уравнение
будет иметь 4 решения, а при ![]() ни
одного.
ни
одного.
3.Решение упражнений (нечетные пункты) на закрепление темы № 568-573 (нечетные).
4. Домашнее задание № 568-573. (четные пункты). Подведение итогов.
|
Термин |
Значение |
|
|
|
|
Арккосинус числа |
- это такое число α, что косинус этого α равен этому числу а. |
|
|
|
|
|
|
|
|
|
|
|
|
3. Контролирующий блок
Тема: Уравнение cos x =a.
|
№ п/п |
1 вариант |
2 вариант |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.