
Уравнения из материалов ЕГЭ профильного уровня смешанного тип
Иррациональные и тригонометрические уравнения.
1. а) Решите
уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Решим уравнение
![]()
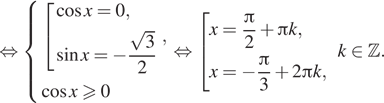
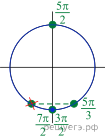
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку ![]() Получим
числа:
Получим
числа: ![]()
Ответ: а) ![]() б)
б)
![]()
2. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Воспользуемся тем, что
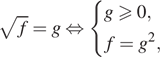
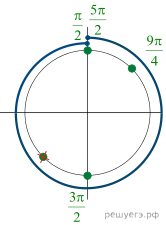
и произведем эквивалентые преобразования уравнения:
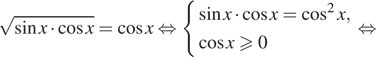
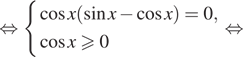
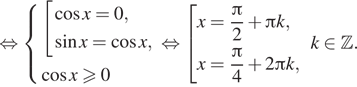
б) Отберем корни при помощи единичной окружности.
Подходят ![]()
Ответ: а) ![]() б)
б)
![]()
3. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Заметим, что
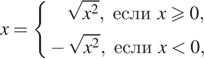
поэтому, внося ![]() под знак корня, необходимо
рассмотреть два случая:
под знак корня, необходимо
рассмотреть два случая:

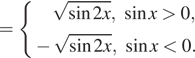
В случае ![]() имеем:
имеем:
![]()
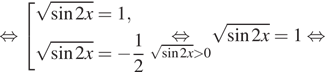
![]()
Условию ![]() удовлетворяет
серия
удовлетворяет
серия ![]()
В случае ![]() имеем:
имеем:
![]()
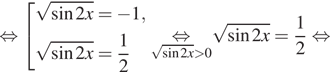
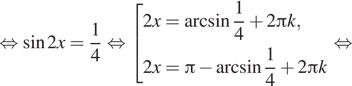
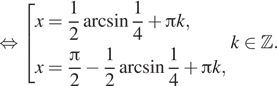
Условию ![]() удовлетворяют
серии
удовлетворяют
серии ![]() и
и
![]()
![]()
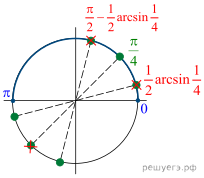
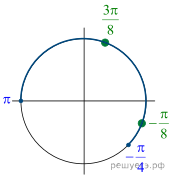
б) Отберём корни, принадлежащие отрезку ![]() при помощи
тригонометрической окружности (см. рис.). Получим
при помощи
тригонометрической окружности (см. рис.). Получим ![]()
Ответ: а) ![]() б)
б)
![]()
4. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. Уравнение имеет корни,
только если ![]() При этом
условии обе части уравнения неотрицательны и можно возвести их в квадрат.
Выполним преобразования:
При этом
условии обе части уравнения неотрицательны и можно возвести их в квадрат.
Выполним преобразования:
![]()
![]()
![]()
![]()
![]()
![]()
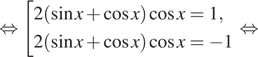
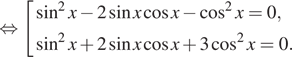
 Разделим второе
уравнение совокупности на
Разделим второе
уравнение совокупности на ![]() получим
получим ![]() это уравнение не имеет
решений. Умножим обе части первого уравнения на −1 и воспользуемся
формулами двойного угла. Получим:
это уравнение не имеет
решений. Умножим обе части первого уравнения на −1 и воспользуемся
формулами двойного угла. Получим:
![]()
![]()
Из найденных серий условию ![]() удовлетворяют
только
удовлетворяют
только ![]() и
и
![]()
Отберем корни при помощи тригонометрической окружности
(см. рис.), получим числа ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]() и
и ![]()
5. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения принадлежащие
отрезку ![]()
Решение. а) Заметим,
что ![]() получим
в левой части
получим
в левой части
![]()
Далее, используя формулы ![]()
![]()
![]() перейдем
к половинному аргументу в правой части и сведем уравнение к однородному
тригонометрическому второй степени:
перейдем
к половинному аргументу в правой части и сведем уравнение к однородному
тригонометрическому второй степени:
![]()
![]()
![]()
![]()

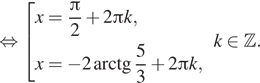
б) Отберем корни при помощи единичной окружности,
подходят ![]()
Ответ: а) ![]() б)
б)
![]()
6. а) Решите
уравнение 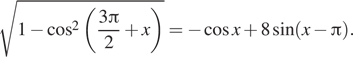
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение с помощью формул приведения и основного тригонометрического тождества:
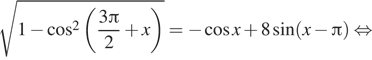
![]()
![]()
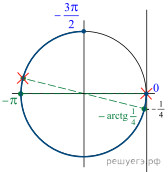
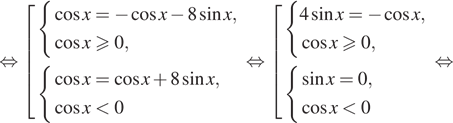
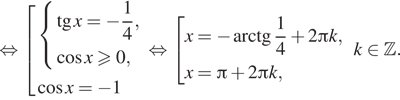
б) Отберём корни. принадлежащие отрезку. Для первой серии получаем:
![]()
![]()
откуда корень ![]() Для
второй серии имеем:
Для
второй серии имеем:
![]()
откуда корень ![]()
Ответ: а) ![]() б)
б)
![]()
7. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 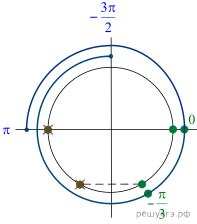 а) При
условии
а) При
условии ![]() исходное
уравнение равносильно следующим:
исходное
уравнение равносильно следующим:
![]()
![]()
![]()
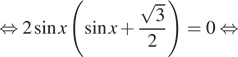
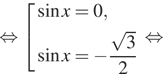
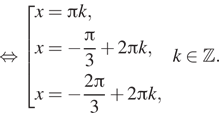
Условию ![]() удовлетворяет
только
удовлетворяет
только ![]()
![]()
![]()
б) Отберем корни при помощи единичной окружности,
подходят ![]() и 0.
и 0.
Ответ: а) ![]() б)
б)
![]() 0.
0.
8. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Левая часть уравнения обращается в нуль в двух случаях. Если второй множитель равен нулю:
![]()
Или если первый множитель равен нулю, а второй при этом определён.
Решим уравнение:
![]()
![]()
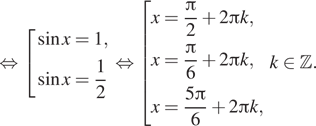
Решим неравенство:
![]()
Неравенству удовлетворяют только корни серии ![]()
Объединяя два рассмотренных случая, заключаем, что решениями
уравнения являются ![]() и
и ![]()
![]()
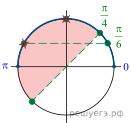
б) Для отбора корней воспользуемся тригонометрической
окружностью (см. рис.). На отрезке ![]() лежат корни
лежат корни ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
9. а) Решите
уравнение 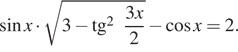
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Перенесем
![]() в правую часть, заметим, что сумма
в правую часть, заметим, что сумма ![]() не
принимает отрицательных значений. Следовательно, при условии
не
принимает отрицательных значений. Следовательно, при условии ![]() возведение обеих частей уравнения в квадрат
является равносильным преобразованием. Имеем:
возведение обеих частей уравнения в квадрат
является равносильным преобразованием. Имеем:
![]()
Выразим множители, стоящие в левой части уравнения, через ![]() В силу основного тригонометрического тождества
В силу основного тригонометрического тождества ![]() Чтобы преобразовать
первый множитель, воспользуемся формулой
Чтобы преобразовать
первый множитель, воспользуемся формулой ![]() откуда
получим:
откуда
получим: 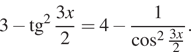 Далее
применим формулы косинуса тройного угла
Далее
применим формулы косинуса тройного угла ![]() и
косинуса половинного угла
и
косинуса половинного угла ![]()
![]()
![]()
Пусть ![]() тогда имеем:
тогда имеем:
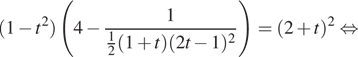
![]()
![]()
![]()
![]()
![]()
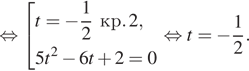
Вернемся к исходной переменной, получим уравнение ![]() откуда
откуда
![]() Учитывая
условие
Учитывая
условие ![]() окончательно
получаем:
окончательно
получаем: ![]()
б) Чтобы найти корни на заданном отрезке, решим двойное неравенство:
![]()
![]()
Так как ![]() правая часть
полученного двойного неравенства лежит в интервале (−1; 0). Значения k
целые, поэтому наибольшее значение k = −1. Оценим
левую часть:
правая часть
полученного двойного неравенства лежит в интервале (−1; 0). Значения k
целые, поэтому наибольшее значение k = −1. Оценим
левую часть:
![]()
Поскольку ![]() подходит
также значение k = −2. Поскольку
подходит
также значение k = −2. Поскольку ![]() осталось
проверить значение k = −3. Покажем, что
осталось
проверить значение k = −3. Покажем, что ![]()
![]()
Итак k = −3, k = −2
или k = −1. Найденным значениям k соответствуют
корни ![]()
![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
10. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 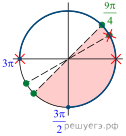 а) При
условии
а) При
условии ![]() и
и
![]() исходное уравнение эквивалентно совокупности
исходное уравнение эквивалентно совокупности

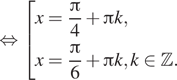
Условию удовлетворяют серии корней ![]() и
и ![]()
б) Отберём корни при помощи единичной
тригонометрической окружности. На заданном отрезке лежит только один
корень — число ![]()
Ответ: а) ![]() б)
б)
![]()
11. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
промежутку ![]()
Решение. 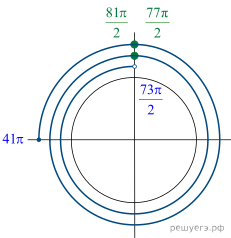 a) Уравнение
a) Уравнение
![]() равносильно уравнению
равносильно уравнению ![]() при
условии
при
условии ![]() Возведем обе
части исходного уравнения в квадрат при условии
Возведем обе
части исходного уравнения в квадрат при условии ![]() получим:
получим:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Полученный корень удовлетворяет исходному ограничению.
б) Отберем корни при помощи единичной окружности
(см. рис.), подходят числа ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
12. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 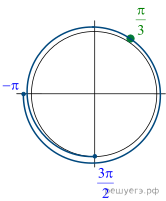 а) Под
знаками обоих радикалов находятся полные квадраты:
а) Под
знаками обоих радикалов находятся полные квадраты:
![]()
![]()
![]()
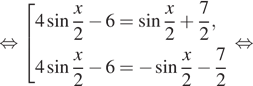
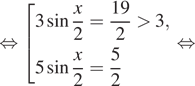
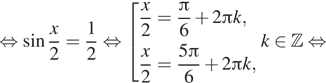
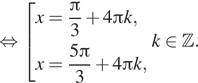
б) Отберём корни при помощи единичной окружности.
Подходит ![]()
Ответ: а) ![]() б)
б)
![]()
13. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Сделаем
замену переменной ![]() тогда:
тогда:
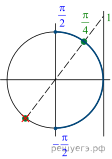
![]()
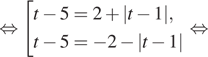
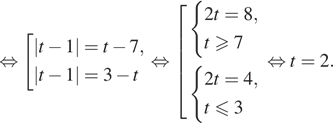
Таким образом, ![]() откуда
откуда ![]()
б) Отберем корни при помощи единичной окружности.
Точка ![]() удовлетворяет
заданному интервалу.
удовлетворяет
заданному интервалу.
Ответ: а) ![]() б)
б)
![]()
Примечание.
Уравнение ![]() удобно
решить, используя геометрический смысл модуля. Действительно, с геометрической
точки зрения левая часть уравнения представляет собой разность расстояний от
точки с координатой t до точек с координатами 5 и 1 на числовой
оси. Эта разность равна в точке
удобно
решить, используя геометрический смысл модуля. Действительно, с геометрической
точки зрения левая часть уравнения представляет собой разность расстояний от
точки с координатой t до точек с координатами 5 и 1 на числовой
оси. Эта разность равна в точке ![]() для точек, лежащих на
числовой оси правее числа 2, эта разность расстояний будет меньше двух, а для
точек, лежащих левее — больше двух.
для точек, лежащих на
числовой оси правее числа 2, эта разность расстояний будет меньше двух, а для
точек, лежащих левее — больше двух.
14. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 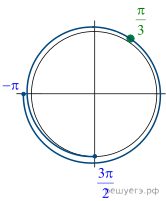 а) Под
знаками обоих радикалов находятся полные квадраты:
а) Под
знаками обоих радикалов находятся полные квадраты:
![]()
![]()
![]()
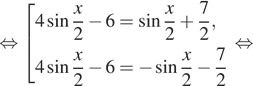
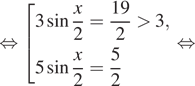
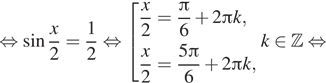
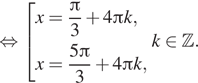
б) Отберём корни при помощи единичной окружности.
Подходит ![]()
Ответ: а) ![]() б)
б)
![]()
15. а) Решите
уравнение 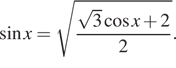
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Преобразуем уравнение:
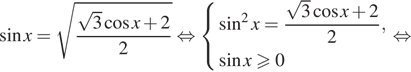
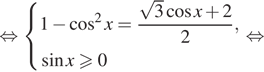
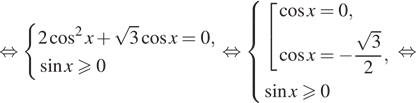
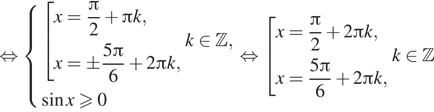
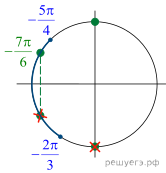
б) Отберём корни при помощи единичной окружности.
Подходит ![]()
Ответ: а) ![]() б)
б)
![]()
16. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 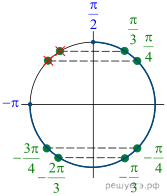 а) Исходное
уравнение имеет смысл только при
а) Исходное
уравнение имеет смысл только при ![]() тогда
это эквивалентно совокупности:
тогда
это эквивалентно совокупности:
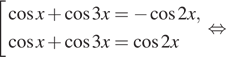
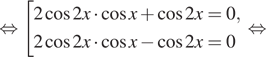
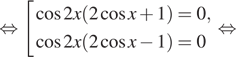
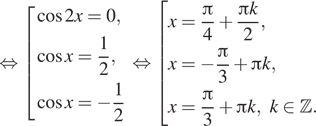
Все найденные серии корней удовлетворяют условию ![]()
б) Отберем корни при помощи единичной окружности
(см. рис.), получим: ![]()
![]()
![]()
![]()
![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
![]()
![]()
![]()
![]() и
и ![]()
17. а) Решите
уравнение 
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. 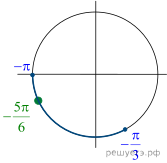 а) Преобразуем
уравнение:
а) Преобразуем
уравнение:

![]()
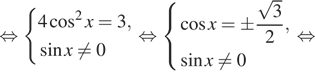
![]()
б) Отберём корни при помощи единичной окружности.
Получим ![]()
Ответ: а) ![]() б)
б)
![]()
18. а) Решите
уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) При
условии ![]() исходное
уравнение эквивалентно следующим:
исходное
уравнение эквивалентно следующим:
![]()
![]()
Каждое из слагаемых в левой части не меньше −1, поэтому их
сумма равна −2 тогда и только тогда, когда каждое слагаемое равно
−1. Решим уравнение ![]() получим
получим ![]() то есть
то есть ![]() Проверим
для найденных решений выполнение условия
Проверим
для найденных решений выполнение условия ![]() Используем
периодичность синуса, применим формулу приведения, получаем:
Используем
периодичность синуса, применим формулу приведения, получаем:
![]()
![]()
Выражение ![]() равно −1 для
всех нечетных k и только для них. Следовательно, решениями уравнения
(⁎) являются числа
равно −1 для
всех нечетных k и только для них. Следовательно, решениями уравнения
(⁎) являются числа ![]() где k —
любое нечетное число. Эти числа удовлетворяют условию
где k —
любое нечетное число. Эти числа удовлетворяют условию ![]() поскольку обращают косинус в нуль. Тем
самым все они являются корнями исходного уравнения.
поскольку обращают косинус в нуль. Тем
самым все они являются корнями исходного уравнения.
б) Решим двойное неравенство:
![]()
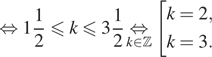
Следовательно, k = 3 и подходит корень ![]()
Ответ: а) ![]() б)
б)
![]()
Примечание.Ответ к пункту а) можно записать в виде ![]()
19. а) Решите
уравнение 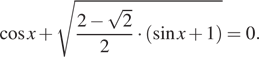
б) Найдите все корни уравнения, принадлежащие отрезку
![]()
Решение. 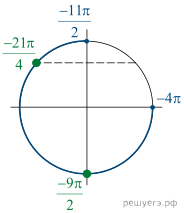 а) Заметим, что
уравнение может иметь решения только при
а) Заметим, что
уравнение может иметь решения только при ![]() Преобразуем его при этом условии:
Преобразуем его при этом условии:
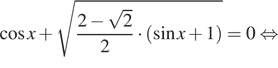

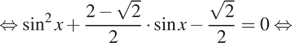
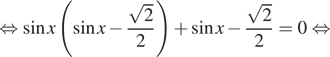

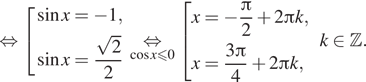
б) Отберём корни, принадлежащие отрезку ![]() при
помощи тригонометрической окружности. Подходят
при
помощи тригонометрической окружности. Подходят ![]()
![]()
Ответ: а) ![]() б)
б)
![]()
![]()
20. а) Решите
уравнение ![]()
б) Найдите все корни уравнения, принадлежащие отрезку
![]()
Решение. а) Знаменатель дроби должен быть отличен от нуля, то есть
![]()
При этом условии числитель дроби должен быть равен нулю. Применим
формулы ![]() и
и ![]() получим:
получим:
![]()
![]()
![]()
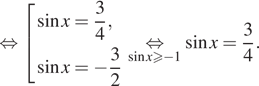
Если ![]() и угол х
лежит в первой четверти, то
и угол х
лежит в первой четверти, то 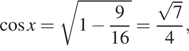 а
тогда
а
тогда ![]() что
обращает знаменатель в нуль. Если же
что
обращает знаменатель в нуль. Если же ![]() и угол х
лежит во второй четверти, то
и угол х
лежит во второй четверти, то 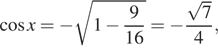 а
тогда
а
тогда ![]() что
допустимо. Следовательно, решением уравнения является серия
что
допустимо. Следовательно, решением уравнения является серия ![]()
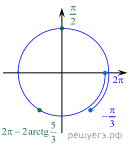
б) Отберем корни, решая двойное неравенство:
![]()
![]()
Акрсинус положительного числа лежит в интервале ![]() поэтому
левая часть двойного неравенства больше –5π, а
правая — меньше –4,5π. Следовательно, число 2πk
лежит в интервале (–5π; –4,5π), а значит,
поэтому
левая часть двойного неравенства больше –5π, а
правая — меньше –4,5π. Следовательно, число 2πk
лежит в интервале (–5π; –4,5π), а значит, ![]() Найденному значению параметра соответствует корень
Найденному значению параметра соответствует корень ![]()
Ответ: а) ![]() б)
б)
![]()
Решить самостоятельно.
1. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
промежутку ![]()
2. а) Решите уравнение 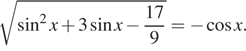
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
3. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
4. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
5. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
промежутку ![]()
6. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
7. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
8. а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Ответы.
1. а) ![]() б)
б)
![]() (№17)
(№17)
2. : а) ![]() б)
б)
![]()
![]() (№40)
(№40)
3. : а) ![]() б)
б)
![]() (№31)
(№31)
4. : а) ![]() б)
б)
![]() (№47)
(№47)
5. : а) ![]() б)
б)
![]() (№55)
(№55)
6. а) ![]() б)
б)
![]() (№67)
(№67)
7. а) ![]() б)
б)
![]()
![]() (№68)
(№68)
8. : а) ![]() б)
б)
![]()
![]()
![]() 0. (№71)
0. (№71)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.