Урок 10_КР_Векторы в пространстве_2

УРОК № 10

Тема урока: Контрольная работа по теме «Векторы в пространстве».

Цель урока:  проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

1. Организационный момент

Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.

2. Контрольная работа

   Задания I уровня сложности

Вариант 1

1.     Вопрос. Сформулируйте определения вектора, его длины, коллинеарности двух ненулевых векторов, равенства векторов. Проиллюстрируйте их, используя изображения параллелепипеда.

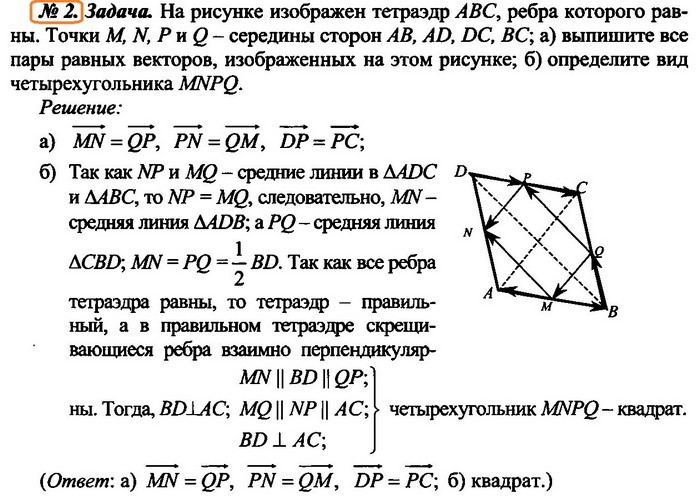
2.     Задача. На рисунке изображен тетраэдр АВС, ребра которого равны. Точки М, N, P и Q — середины сторон АВ, AD, DC, ВС;
а) выпишите все пары равных векторов, изображенных на этом рисунке;
б) определите вид четырехугольника MNPQ.

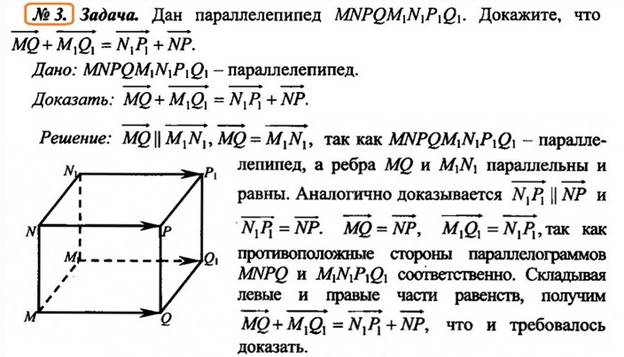
3.     Задача. Дан параллелепипед MNPQM₁N₁P₁Q₁. Докажите, что .

Вариант 2

1.     Вопрос. Расскажите о правиле треугольника сложения двух векторов. Проиллюстрируйте эти правила на рисунке.

2.     Задача. Упростите выражение: .

3.     Задача. Дан параллелепипед MNPQM₁N₁P₁Q₁. Докажите, что

   Задания II уровня сложности

Вариант 1

1.     Вопрос. Расскажите о правиле параллелограмма сложения двух векторов. Проиллюстрируйте это правило на рисунке.

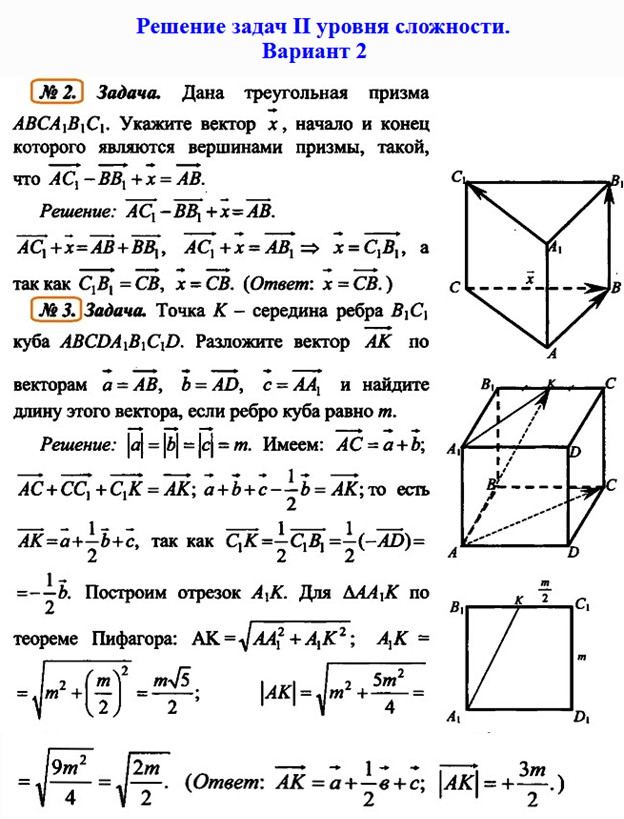
2.     Задача. Дана треугольная призма АВСА₁В₁С₁. Укажите вектор х, начало и конец которого являются вершинами призмы, такой, что .

3.     Задача. Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали которого пересекаются в точке М. Разложите векторы  по векторам .

Вариант 2

1.     Вопрос. Расскажите о правиле многоугольника сложения нескольких векторов. Проиллюстрируйте его на рисунке.

2.     Задача. Дана треугольная призма АВСА₁В₁С₁. Укажите вектор х, начало и конец которого являются вершинами призмы, такой, что .

3.     Задача. Точка К — середина ребра В₁С₁ куба ABCDA₁B₁C₁D. Разложите вектор  по векторам  и найдите длину этого вектора, если ребро куба равно m.

   Задания III уровня сложности

Вариант 1

1.     Вопрос. Сформулируйте определение произведения вектора а на число k, сочетательный, первый и второй распределительные законы умножения вектора на число. Проиллюстрируйте их на примерах.

2.     Задача. На рисунке изображен правильный октаэдр. Докажите, что .

3.     Задача. Точки А₁, В₁, С₁ — середины сторон ВС, АС, АВ треугольника АВС, точка О — произвольная точка пространства. Докажите, что .

Вариант 2

1.     Вопрос. Сформулируйте определение компланарных векторов. Приведите примеры компланарных и некомпланарных векторов, используя изображение параллелепипеда.

2.     Задача. Дан параллелепипед ABCDA₁B₁C₁D₁. Найдите сумму векторов .

3.     Задача. В тетраэдре ABCD точка К — середина медианы ВВ₁ грани BCD. Разложите вектор  по векторам .

4.     Рефлексия учебной деятельности.

В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.

Домашнее задание: решить задачи, с которыми ученик не справился.

   Решение задач I уровня сложности.
Вариант 1

3.     Задача. Точки А₁, В₁, С₁ — середины сторон ВС, АС, АВ треугольника АВС, точка О — произвольная точка пространства. Докажите, что .

Вариант 2

1.     Вопрос. Сформулируйте определение компланарных векторов. Приведите примеры компланарных и некомпланарных векторов, используя изображение параллелепипеда.

2.     Задача. Дан параллелепипед ABCDA₁B₁C₁D₁. Найдите сумму векторов .

3.     Задача. В тетраэдре ABCD точка К — середина медианы ВВ₁ грани BCD. Разложите вектор  по векторам .