Урок Алгебры и начала математического анализа, 10 класс, тема "Тригонометрические функции двойного угла"

Урок по алгебре и началам анализа в 10 классе в условиях использования проблемного обучения

Учитель Тараканова Оксана Валентиновна, 1 квалификационная категория, Лицей № 11 ОАО «РЖД»

Тема урока Тригонометрические функции двойного угла

Тип урока Урок открытия новых знаний.

Формируемые результаты

Предметные: формировать умения выводить и применять формулы двойного угла.

Личностные: формировать умение планировать свои действия в соответствии с учебным заданием.

Метапредметные: формировать умения устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации.

Планируемые результаты

Учащийся научится выводить и применять формулы двойного угла.

Основные понятия

Формулы двойного угла, формула косинуса двойного угла, формула синуса двойного угла, формула тангенса двойного угла, косинус разности, косинус суммы, синус разности, синус суммы, тангенс разности, тангенс суммы.

I.                   Организационный этап

II.                 Постановка формируемых результатов урока. Мотивация учебной деятельности учащихся
Эпиграфом нашего урока будут слова Бернардо Больцано (чешский математик и философ) «Формула подчас кажется более мудрой, чем выдумавший её человек».

Мы живём в реальном мире, и для его познания нам необходимы новые знания. Сегодня мы поднимемся на следующую ступеньку ваших знаний по теме «Тригонометрия»

III.             Актуализация знания

Для успешной работы выполним некоторые задания:

Разминка: Какие мнемонические правила надо вспомнить для применения формул синуса суммы или косинуса суммы? (синнакос/кокос)

№ 485(1,4)

1)      Sin73°Cos17° + Sin17°Cos73° = Sin(73° + 17°) = Sin90° = 1

2)      Sin – Sin= Sin( – ) = Sin = Sin = 1

№ 482 (1,3)

1)      Cos(57°30´)Cos(27°30´) + Sin(57°30´)Sin(27°30´) = Cos(57°30´ - 27°30´) =
= Cos30° = /2

3)      Cos Cos  – SinSin = Cos) = Cos 2π = 1

Вычислить:  2Sin15°Cos15° = ? (*)

·         В чём проблема?

·         Достаточно ли знаний, чтобы справиться с этим заданием?

·         Почему возникли затруднения?

IV.             Изучение нового материала

      Пришло время подняться на следующую ступеньку.

Давайте это выражение пока оставим и вернёмся к нему позже.

Вспомним ещё раз формулы косинуса и синуса суммы аргументов (на экране)

Sin (α+β) = Sinα Cosβ + Sinβ Cosα

 Cos (α+β) = Cosα Cosβ – Sinα Sinβ

Могут ли в данных формулах углы быть равными? (Да)

Как тогда будут выглядеть левая часть выражения? (учащиеся пробуют подставить в формулу вместо β значение α) (два ученика работают на доске)

Sin(α+α) = Sin2α

Cos(α+α) = Cos2α

Как можно назвать полученные выражения? (Синус двойного угла и косинус двойного угла)

Это и есть тема нашего урока. Откройте тетради, запишите число и тему урока  (появляется тема на слайде).

Данные формулы справедливы для любых значений углов. Формулы работают как слева направо, так и справа налево.

Какова цель дальнейшей работы на уроке? (вывести формулы, научиться их применять)

Я предлагаю вывести формулы двойного угла, используя формулы суммы.

Даю 2 минуты на самостоятельную работу. Продолжите начатые записи, применяя формулы суммы.

Sin(α+α) = Sin2α = Sinα Cosα + Sinα Cosα = 2 Sinα Cosα

Cos(α+α) = Cos2α = Cosα Cosα – Sinα Sinα = Cos²α – Sin²α

Запишите на доске полученные результаты.

Sin2α=2SinαCosα

Cos2α=Cos²α-Sin²α

Прочитайте формулу. У всех так получилось?

Сравним наши результаты с учебником.

Откройте стр. 149.

Эти формулы называются синусом двойного угла и косинусом двойного угла.

 Вернёмся к выражению (*).

Можете ли вы теперь найти значение этого выражения?

Найдите. (Один человек у доски, остальные в тетради оформляют решение)
2Sin15°Cos15° = Sin (2*15⁰) = Sin 30⁰ = 0.5

Знание формул помогает выбрать наиболее рациональный метод решения заданий. Вернёмся к вчерашнему решению Тани Ш. (на экране сохранённое решение). Можно ли выполнить это задание, используя формулы двойного угла? Кто выйдет к доске и упростит выражение? (Один ученик выходит к доске и выполняет преобразование по новой формуле)

Сравните решение Татьяны с новым решением. Какое решение короче? Более короткое решение в математике является наиболее рациональным, т.к.  оно экономит время, что очень актуально на экзамене.

V.                Первичное закрепление нового материала

Рассмотрим задания ЕГЭ. (На партах лежат листы с заданиями из ЕГЭ).

Найдите те задания, в которых можно применить формулы двойного угла. Отметьте их номера. Даю минуту на размышление. Готовы? Озвучьте их номера. Сравните с моими вариантами, проверьте себя. (Ответ: 1, 2, 3, 4, 6, 7, 8, 9)

1.   Найдите , если  Ответ: 22,08

2.   Найдите  если  и  Ответ: -0,96

3.   Найдите значение выражения  Ответ: 6

4.   Найдите , если Ответ: -7

5.   Найдите значение выражения:  Ответ: 32

6.   Найдите значение выражения 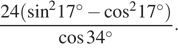  Ответ: -24

7.   Найдите значение выражения    Ответ: -1,5

8.       Найдите значение выражения  Ответ: −1,25.

9.   Найдите , если   Ответ: 4

10.  Найдите значение выражения  Ответ: 59

Задания отобрали, теперь необходимо их решить. Все задания разной степени сложности. Какой достанется вам, решит жребий. От каждой пары по очереди тянем свой счастливый номер (на столе учителя лежат номерки 1, 2, 3, 4, 6, 7, 8, 9).

Работая в  парах, выполните задание в течение 3-х минут. Кто готов, выходит к доске и оформляет решение.

Группы готовы представить решение своего задания? Во время защиты учащиеся из других групп переносят решение заданий себе в тетрадь. По ходу защиты можно задавать вопросы.

VI.             Итоги урока (Рефлексия)

Итак, ребята, с какими новыми формулами мы сегодня познакомились? Кто сегодня испытал трудности в применении новых формул? Была ли достигнута цель на уроке? (Частично, т.к. мы не рассмотрели тангенс двойного угла). Каким тогда может быть домашнее задание?

VII.          Информация о домашнем задании

§29. Выучить формулы, вывести формулу тангенса двойного угла, №500, 501, 502, 503