Урок физики в 10 классе: «Идеальный газ в молекулярно-кинетической теории. Основное уравнение молекулярно- кинетической теории газа»

Урок в 10 классе

Тема: «Идеальный газ в молекулярно-кинетической теории. Основное уравнение молекулярно- кинетической теории газа.»

Цель:

Познавательная: дать основные понятия идеального газа и основного уравнения МКТ

Обучающая: объяснить связь между энергией и температурой

Воспитательная: воспитание научного мировоззрения.

Ход урока

1.      Оргмомент

2.      Проверка д.з.

3.      Постановка целей и задач урока.

4.      Объяснение нового материала.

Идеальный газ – это газ со следующими свойствами:

1.      Размеры молекул малы по сравнению со средним расстоянием между ними; молекулы можно принять за материальные точки;

2.      Силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях;

3.      Молекулы сталкиваются друг с другом как абсолютно упругие шары, движение которых описывается законами классической механики (в этом случае принимать молекулы за материальные точки нельзя).

На основании этой модели можно объяснить, почему газ занимает весь предоставленный ему объём, лёгкую сжимаемость газов, давление, которое оказывает газ на стенки сосудов, газовые законы.

Как и любая модель, модель идеального газа имеет свои ограничения. Она применима при небольших давлениях (менее 100 атм) и не очень низких температурах.

Характеристики газа.

Для описания состояния газа можно воспользоваться микропараметрами. Это – масса и скорость молекул, энергия и импульс молекул, их концентрация. Данные параметры являются индивидуальными характеристиками молекул. Найти их с помощью простых измерительных приборов невозможно. Гораздо большую практическую роль играют макропараметры. Значения макропараметров определяются совместным действием огромного количества молекул, и измерить их можно, используя достаточно простые приборы.

Три макропараметра – объём, давление и температура – позволяют описать состояние любой газовой системы.

Под объёмом газа понимают объём сосуда, в котором находится газ.

Единица измерения объёма в системе СИ – 1 м³.

Давление газа – это средняя сила ударов молекул о стенки сосуда, приходящаяся на единицу поверхности стенки.

Единица измерения давления в системе СИ – 1 паскаль.

1 паскаль – это давление, при котором на площадь поверхности 1 м² действует сила в 1 Н, направленная перпендикулярно поверхности.

Внесистемная единица измерения давления – физическая атмосфера.

1 атм=10⁵ Па

Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа - это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:

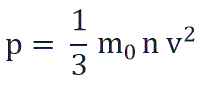
p – давление молекул газа на границы емкости,

m₀ – масса одной молекулы,

n - концентрация молекул, число частиц N в единице объема V;

v² - средне квадратичная скорость молекул.

Вывод основного уравнения МКТ

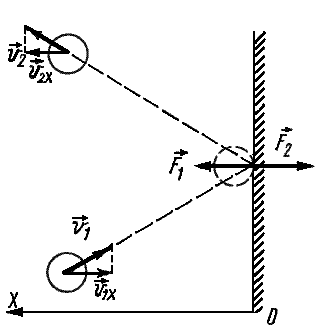
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция v_x скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:

Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv_1x = –mv_x на mv_2x = mv_x.

Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:

Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:

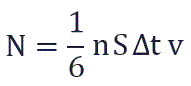
S – площадь этой стенки

n - концентрация частиц

Давление p равно отношению силы F к площади S, на которую действует эта сила:

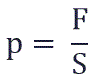
Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:

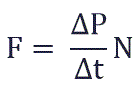
Исходя из вышенаписанного получаем:

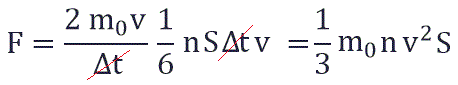
Тогда

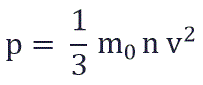
Если заменить среднее значение кинетической энергии поступательного движения молекул - E:

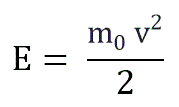
и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:

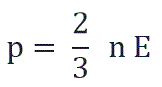
Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.

5.      Закрепление – решение задач

1. При неизменной концентрации молекул гелия средняя кинетическая энергия теплового движения его молекул уменьшилась в 4 раза. При этом давление газа:

1) уменьшилось в 16 раз

2) уменьшилось в 2 раза

3) уменьшилось  в 4 раза

4) не изменилось

Согласно основному уравнению МКТ, давление p прямо пропорционально средней кинетической энергии поступательного движения молекул: . Если правая часть уравнения уменьшается в 4 раза, то и левая должна тоже уменьшится в 4 раза, ответ: 3.

2. Давление газа зависит от:

А) концентрации молекул

Б) средней кинетической энергии молекул

Выберите верный вариант:

1) только от А            2) только от Б              3) и от А, и от Б                4)ни от А, ни от Б

Правильный ответ – 3, согласно основному уравнению МКТ, см. предыдущую задачу.

3. В результате остывания газа средняя кинетическая энергия теплового движения его молекул уменьшилась в три раза. При этом абсолютная температура газа:

1) уменьшилась в 3 раза

2) уменьшилась в 9 раз

3) уменьшилось  в   раз

4) не изменилась

Из основного уравнения МКТ:   и определения абсолютной температуры:  имеем:  – средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре. Таким образом, если энергия уменьшилась втрое, то и температура – тоже уменьшилась втрое.

Ответ: 1.

4. В результате нагревания идеального газа  его давление при постоянной концентрации молекул увеличилось в два раза. При этом абсолютная температура газа:

1) увеличилась в 4 раза

2) увеличилась в 2 раза

3) уменьшилось  в  2 раза

4) не изменилась

Согласно зависимости давления газа от абсолютной температуры Т и концентрации его молекул:    давление прямо зависит от температуры, и наоборот. Тогда при увеличении давления вдвое температура тоже увеличилась вдвое.

Ответ: 2.

5. При по­ни­же­нии тем­пе­ра­ту­ры газа в за­па­ян­ном со­су­де дав­ле­ние газа умень­ша­ет­ся. Это умень­ше­ние дав­ле­ния объ­яс­ня­ет­ся тем, что

1) умень­ша­ет­ся объём со­су­да за счет осты­ва­ния его сте­нок
2) умень­ша­ет­ся энер­гия теп­ло­во­го дви­же­ния молекул газа
3) умень­ша­ют­ся раз­ме­ры мо­ле­кул газа при его охла­жде­нии
4) умень­ша­ет­ся энер­гия вза­и­мо­дей­ствия мо­ле­кул газа друг с дру­гом

Объем сосуда может измениться вследствие уменьшения давления газа при понижении температуры – так стенки канистры, если в ней был бензин и остались его пары, втягиваются внутрь при похолодании. Но за счет остывания стенок мы это вряд ли заметим невооруженным глазом.

Размеры молекул – величина постоянная и не меняется ни с температурой, ни по другим причинам.

Энергия взаимодействия молекул газа друг с другом определяется их средней кинетической энергией, которая-то и зависит от температуры: , .

Ответ: 2.

6. На гра­фи­ке по­ка­за­на за­ви­си­мость дав­ле­ния от кон­цен­тра­ции для двух иде­аль­ных газов при фик­си­ро­ван­ных тем­пе­ра­ту­рах. От­но­ше­ние тем­пе­ра­тур  этих газов равно

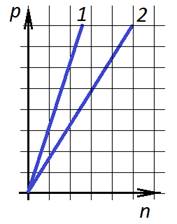
1) 1

2) 2
3) 0,5
4) 

Согласно уравнению идеального газа  . Выразим температуру:  

Для первого газа: 

Для второго газа: 

Отношение температур тогда: . Возьмем точки на графиках, у которых давление одинаковое, тогда:

 . Во взятых точках концентрация молекул второго газа вдвое больше, чем первого. Тогда  .

Ответ: 2.

7. На гра­фи­ках пред­став­ле­ны за­ви­си­мо­сти кон­цен­тра­ции  n и тем­пе­ра­ту­ры T  иде­аль­но­го газа от вре­ме­ни. Из этих за­ви­си­мо­стей сле­ду­ет, что дав­ле­ние газа с те­че­ни­ем вре­ме­ни

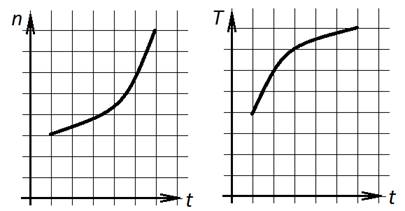1) уве­ли­чи­ва­лось
2) умень­ша­лось
3) не из­ме­ня­лось
4) сна­ча­ла уве­ли­чи­ва­лось, а потом из­ме­ня­лось

 Согласно уравнению идеального газа   давление прямо пропорционально как концентрации, так и температуре. Значит, раз и температура растет, и концентрация – значит, давление все время растет.

Ответ: 1.

8. В ре­зуль­та­те охла­жде­ния од­но­атом­но­го иде­аль­но­го газа его дав­ле­ние умень­ши­лось в 4 раза, а кон­цен­тра­ция мо­ле­кул газа не из­ме­ни­лась. При этом сред­няя ки­не­ти­че­ская энер­гия теп­ло­во­го дви­же­ния мо­ле­кул газа

1) умень­ши­лась в 16 раз
2) умень­ши­лась в 2 раза
3) умень­ши­лась в 4 раза
4) не из­ме­ни­лась

Давление газа зависит от средней кинетической энергии теплового движения молекул так: . Тогда, если левая часть уравнения уменьшена в 4 раза, то и правая должна уменьшиться во  столько же раз. При этом мы знаем, что концентрация не менялась – значит, уменьшилась вчетверо средняя кинетическая энергия теплового движения молекул.

6.      Выводы по уроку

7.      Домашнее задание по учебнику